2. 太原科技大学 电子信息工程学院, 太原 030024
针对描述密集传感器网络k覆盖问题感知模型的不足,结合传感器节点空间分布的泊松点特征及信道传输特性,采用积分几何集合相交的方法,提出了一种基于瑞利信道的传感器网络节点覆盖测度模型,并推导了网络k覆盖概率及达到k覆盖所需的节点密度. 通过仿真实验分析了信道参数对k覆盖概率的影响,验证了测度模型的正确性.
2. Department of Electronic Information Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China
A new coverage measure model in dense wireless sensor network was proposed in Rayleigh fading channel, which is more suitable to the actual transmit environment compared to existing sensing models. The spatial distribution of sensors are modeled as a Poisson point process, and the Rayleigh fading channel is adopted as the propagation channel. Through the set intersection algorithm from integral geometry, the coverage measure for k-coverage was achieved, the probability for k-coverage and the node density guaranteeing k-coverage were derived. Simulations demonstrate the influence of channel parameters and validate the correctness of the coverage measure model.
大量体积小、成本低、具有感知及无线通信功能的传感器节点被密集地部署于无人到达的区域,用于完成入侵检测、野外环境监测、战场监视等应用.在此类密集传感器网络中,为达到一定的检测质量,需要保证传感器节点对监控目标的k覆盖[1].
在保证k覆盖的密集传感器网络中,由于信道传输环境更加复杂,信号传输的多径效应引起的小尺度衰落令接收信号的包络呈现瑞利分布特性[2],此时,常用来描述覆盖问题节点感知能力的理想圆盘感知模型[3]、仅考虑路径损耗的衰减圆盘感知模型[4]、截断的衰减圆盘感知模型[5]、Elfes感知模型[6]、混合感知模型[7]及随机感知模型[8],显然已不能用来描述节点对监控目标的覆盖测度.笔者将瑞利信道用于对密集传感器网络的随机k覆盖问题的传输模型建模,结合节点的空间分布特征,将节点对监控目标的覆盖映射为二维平面的集合相交问题,利用积分几何方法得出了一种新的感知测度模型,并推导了网络k覆盖概率的计算过程,得出了满足k覆盖所需的节点密度.通过仿真分析了瑞利信道参数、节点密度对网络k覆盖概率的影响,得出了网络满足k覆盖节点密度的阈值,验证了测度模型的正确性.
1 系统和信道模型假设用于监控应用的传感器节点随机分布于二维欧氏空间$\mathbb{R}$2上,每个发射节点拥有相同的初始能量、感知能力及发射功率.节点的空间位置服从定义在概率空间(Ω,F,P)上的强度为λ的静态齐次泊松点过程ψ= {xi; i=1,2,3,…},其中xi为第i个节点的位置.接收节点独立于ψ,存在功率为W的噪声.假设媒体访问控制层采用有效的调度协议,忽略来自于同时发送信号的传输节点之间的干扰.A是定义在$\mathbb{R}$2上的有界子集,则区域A中存在n个传感器节点的概率为
| $P\left( \left| A\cap \psi \right|\text{=n} \right)=\frac{{{\left( \lambda {{M}_{A}} \right)}^{n}}{{e}^{-\lambda {{M}_{A}}}}}{n!}$ | (1) |
其中:|·| 表示集合的基数,MA为A的面积.用κr-η来表示信道中的路径损耗,η为路损指数. 信道增益定义为h(x,y),h(x,y)服从均值为1/μ的指数分布,h(x,y)~exp(μ),因为节点之间以及监控目标之间位置相互独立,将在后面的讨论中省略掉(x,y).
2 随机k覆盖 2.1 覆盖测度对区域A k覆盖问题的研究,需要解决2个问题,其一是找到描述节点感知特性的感知模型以计算节点对监控目标的覆盖测度,其二是根据测度模型完成对区域k覆盖概率的计算.
对于任意一个传感器xi∈ψ,可以对任意监控目标yj提供覆盖的邻居节点集定义为${{N}_{x}}_{_{i}}=\left\{ {{x}_{i}}\left| \frac{{{P}_{t}}k{{h}_{i}}{{\left\| {{y}_{j}}-{{x}_{i}} \right\|}^{-\eta }}}{W}\ge \beta \right. \right\}$,其中β为信噪比(SNR,signal-to-noise ratio)阈值,Pt为节点的发射功率,κ为取决于物理层的传输常数,hi为瑞利信道衰减因子,W为噪声功率.则节点xi的感知半径R的累积分布函数可以表示为
| $\begin{align} & {{F}_{R}}\left( r \right)=P\left\{ SNR\left( r \right)\ge \beta \right\}=P\left\{ \frac{{{P}_{t}}k{{h}_{i}}{{\left\| {{y}_{j}}-{{x}_{i}} \right\|}^{-\eta }}}{W}\ge \beta \right\}= \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ P\left\{ {{h}_{i}}\ge \frac{\beta W}{{{P}_{t}}\kappa {{\left\| r \right\|}^{\eta }}} \right\}=1-{{F}_{h}}_{_{i}}\left( \frac{\beta W}{{{P}_{t}}\kappa {{\left\| r \right\|}^{\eta }}} \right) \\ \end{align}$ | (2) |
其中:r为节点与监控目标的距离,Fhi(·)表示hi的累积分布函数.当且仅当SNR(r)≥β时,传感器可以检测到距离其为r的目标.由于节点xi的感知区域随信道环境的变化呈现非规则性,将区域A内所有监控目标的集合定义为有界凸集SA,通过求取节点xi感知区域半径R的一阶矩(见式(3))及二阶矩(见式(4))来限定xi邻居节点所在的凸集Si为有界区域.
| ${{\left( \frac{{{P}_{t}}\kappa }{\beta W} \right)}^{\frac{1}{\eta }}}\int{_{0}^{\infty }}\mu {{r}^{\frac{1}{\eta }}}{{e}^{-\mu r}}dr={{\left( \frac{{{P}_{t}}\kappa }{\beta W\mu } \right)}^{\frac{1}{\eta }}}\Gamma \left( 1+\frac{1}{\eta } \right)$ | (3) |
| $\begin{align} & {{E}_{h}}_{_{i}}\left( {{R}^{2}} \right)={{E}_{h}}_{_{i}}\left( {{\left\| r \right\|}^{2}} \right){{}_{{{\left\| \text{r} \right\|}^{\text{2}}}\text{}{{\left( {{P}_{t}}\kappa {{h}_{i}}/\beta W \right)}^{2/\eta }}}}= \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\left( \frac{{{P}_{t}}\kappa }{\beta W} \right)}^{\frac{2}{\eta }}}\int{_{0}^{\infty }}\mu {{r}^{\frac{2}{\eta }}}{{e}^{-\mu r}}dr= \\ & {{\left( \frac{{{P}_{t}}\kappa }{\beta W} \right)}^{\frac{2}{\eta }}}\int{_{0}^{\infty }}{{e}^{-t}}{{t}^{\frac{2}{\eta }}}dt={{\left( \frac{{{P}_{t}}\kappa }{\beta W\mu } \right)}^{\frac{2}{\eta }}}\Gamma \left( 1+\frac{2}{\eta } \right) \\ \end{align}$ | (4) |
其中$\Gamma \left( x \right)\int{_{0}^{\infty }}{{e}^{-t}}{{t}^{\frac{2}{\eta }}}dt$表示伽玛函数.分别用Li和Mi、LA和MA表示凸集Si及SA的周长及面积.可计算出凸集Si的周长Li及面积Mi分别为
| ${{L}_{i}}=2\pi {{E}_{h}}_{_{i}}\left( R \right)$ | (5) |
| ${{M}_{i}}=\pi {{E}_{h}}_{_{i}}\left( {{R}^{2}} \right)$ | (6) |
定义事件e为{A内任意一点p(p∈A)被k个传感器节点覆盖| 区域A内存在n个节点},则Pd(n,k)为事件e在P上的测度. 将节点对区域A的覆盖测度问题映射为积分几何中的集合相交问题[1],则
| $\begin{array}{l} {P_d}\left( {n,k} \right) = \\ \left\{ \begin{array}{l} \prod\limits_{i = 1}^n {\left( {\frac{{2\pi {M_A} + {L_i}{L_A}}}{{2\pi \left( {{M_A} + {M_i}} \right) + {L_i}{L_A}}}} \right)} ,k = 0\\ \sum\limits_{i = 1}^{\left( {\begin{array}{*{20}{c}} n\\ k \end{array}} \right)} {\left( {\prod\limits_{j = 1}^k {\left( {2\pi {M_{T\left( {i,j} \right)}}} \right)\prod\limits_{z = 1}^{n - k} {\left( {2\pi {M_A} + {L_{G\left( {i,z} \right)}}{L_A}} \right)} } } \right),k \ge 1} \end{array} \right. \end{array}$ | (7) |
其中:T表示以从n个节点中选取的k个节点为行j元素的矩阵,G表示以T中没有选中的节点为行z元素的矩阵,MT(i,j)及LG(i,z)分别表示这些节点感知区域的面积及周长. 因网络为同构网络,故MT(i,j)=Mr=Mi,LG(i,z)=Lr=Li,则Pd(n,k)可表示为
| ${{P}_{d}}\left( n,k \right)=\frac{\left( \frac{n}{k} \right){{\left( 2\pi {{M}_{i}} \right)}^{k}}{{\left( 2\pi {{M}_{A}}+{{L}_{r}}{{L}_{A}} \right)}^{n-k}}}{{{\left[2\pi ({{M}_{A}}+{{M}_{i}}){{L}_{i}}{{L}_{A}} \right]}^{n}}}$ | (8) |
本节推导满足密集传感器网络随机k覆盖所需最少节点密度的计算公式.
定义Pexact(λ,k)及Pleast(λ,k)分别表示区域A内任意一点p(p∈A)被k个节点以及至少k个节点覆盖的概率.基于全概率公式,Pexact(λ,k)可表示为
| ${{P}_{exact}}\left( \lambda ,k \right)=\sum\limits_{n=k}^{\infty }{P\left( \left| A\cap \psi \right|\text{=n} \right)}{{P}_{d}}\left( n,k \right)$ | (9) |
Pleast(λ,k)可以通过计算1减去少于k覆盖的概率之和得到,即
| ${{P}_{least}}\left( \lambda ,k \right)=1-\sum\limits_{i=0}^{k-1}{{{P}_{exact}}\left( \lambda ,i \right)}$ | (10) |
当Pleast(λ,k)=q时,计算以概率q满足k覆盖的节点的部署密度λ的表达式为
| $\lambda =\frac{\ln \left( \frac{1-q}{\sum\limits_{i=0}^{k-1}{\left( \begin{align} & n \\ & i \\ \end{align} \right){{\left( 2\pi {{M}_{i}} \right)}^{i}}{{(2\pi {{M}_{A}}+{{L}_{i}}{{L}_{A}})}^{n-i}}}} \right)}{MA\left[\frac{1}{2\pi ({{M}_{A}}+{{M}_{i}}){{L}_{i}}{{L}_{A}}}-1 \right]}$ | (11) |
利用Matlab进行计算机仿真,A取50 m×50 m区域,Pt取1 mW,W取0.01 mW,传输常数κ为10[2],节点分布密度0节点/m2<λ<0.1节点/m2,信道衰减因子0<μ<1,路径损耗因子2<η<6,SNR阈值 (传感器灵敏度参数)0<β<40 dB.
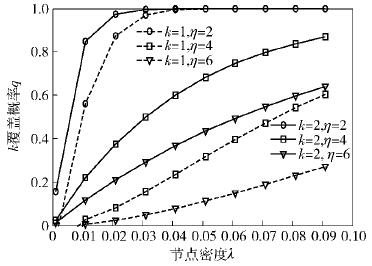
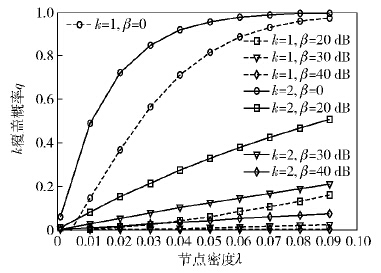
图 1、图 2、图 3分别显示了在不同η、μ及β的取值条件下,区域A内随机1、2覆盖的概率q.对于给定的覆盖概率q和覆盖目标k,可从图 1、图 2、图 3得出所需的节点密度值λ. 当节点密度确定时,从图 1、图 2中看到,随着η、μ的增大,q减小而更靠近横轴. 因为节点的感知区域随η、μ变大而变小,变小的感知区域对区域A覆盖的概率q减小.从图 3中可以看到,q随节点接收灵敏度变大,即随β的变小而靠近于纵轴.因为在给定的节点发射功率下,节点平均感知区域随β变小而增大,会增加节点对区域A的覆盖概率q.
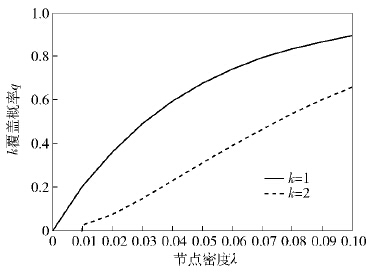
图 4对比了当η=4、μ=1、β=20 dB时,随机1、2覆盖概率q与节点密度的关系. 从图 4中可以看出,要达到某一覆盖概率q,所需节点的密度随着覆盖目标k的增加而增加.
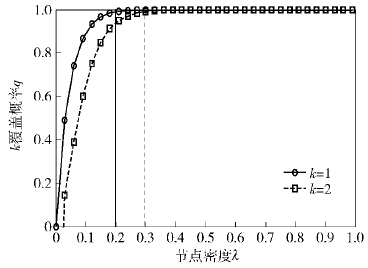
图 5对应η=4、μ=1、β=20 dB时,k覆盖概率q随节点密度的变化趋势.事实上,可通过式(11)计算出满足随机k覆盖概率趋于1的节点密度.图 5通过仿真的方法得到了k=1、2时,覆盖概率q趋于1的节点密度分别为0.2节点/m2(黑色竖线)和0.3节点/m2(虚线). 从图 5中可以看到,保证覆盖概率为1的节点密度阈值随着k的增加而增加,当达到密度阈值后再增加传感器的数量对q的提高没有任何意义.
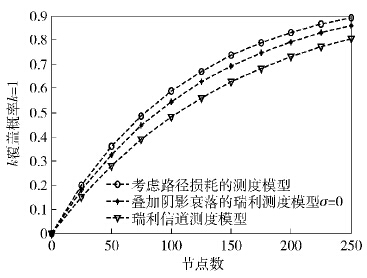
显然,根据图 1、图 2,当η及μ增大,即信道条件恶化时,随机k覆盖的概率更靠近横轴,对应的1、2覆盖的密度阈值会右移.根据图 3,当节点的接收灵敏度增大,即β减小时,随机k覆盖的概率更靠近纵轴,对应的1、2覆盖的密度阈值会左移. 图 6对比了当η=4、μ=1、β=20 dB时,所提出的瑞利信道测度模型与考虑路径损耗的概率模型[2]以及叠加阴影衰落[2]的瑞利信道模型对区域1覆盖概率的影响.
当阴影衰落因子σ =0时,叠加阴影衰落的瑞利信道退化为瑞利信道. 从图 6中可以看到,所提出的感知测度模型得出的1覆盖概率接近于文献[2]中退化瑞利信道的1覆盖概率,区别于文献[2]利用任意节点的节点孤立概率计算区域达到1覆盖的概率. 所提模型从传感器节点感知区域与感兴趣区域被监控点所在集合相交的角度得到了区域的1覆盖概率,考虑了所有传感器节点对区域覆盖的贡献,精确度更高.
4 结束语研究了密集传感器网络中的随机k覆盖问题,将密集传感器网络中节点的信道模型建模为瑞利信道传输模型,结合节点的空间分布特征及积分几何的算法得出了新的适用于k覆盖问题分析的传感器节点对监控目标的覆盖测度,从而得出了网络以概率q满足k覆盖的节点密度计算公式.通过仿真,分析了不同路径损耗指数、信道衰减因子、传感器节点的接收灵敏度对k覆盖概率q的影响,验证了所提覆盖测度模型的正确性.
| [1] | Loukas L, Radha P. Stochastic coverage in heterogeneous sensor networks[J]. ACM Transaction on Sensor Networks, 2006, 2(3): 325-358.[引用本文:1] |
| [2] | Miorandi D. The impact of channel randomness on coverage and connectivity of Ad hoc and sensor networks [J]. Wireless Communications, IEEE Transactions on, 2008, 7(3): 1062-1072.[引用本文:4] |
| [3] | Gupta H P, Rao S V, Venkatesh T. Analysis of stochastic k-coverage in wireless sensor networks with boundary deployment[C]// IEEE WCNC'14. Turkey: IEEE Press, 2014: 2629-2634.[引用本文:1] |
| [4] | Veltri G, Huang Qingfeng, Qu Gang, et al. Minimal and maximal exposure path algorithms forwireless embedded sensor networks[C]// ACM International Conference on Embedded Networked Sensor Systems (SenSys 2003). USA: ACM, 2003: 40-50.[引用本文:1] |
| [5] | Zou Yi, Chakrabarty K. A distributed coverage-and connectivity-centric technique for selecting active nodes in wireless sensor networks[J]. IEEE Transactions on Computers, 2005, 54(8): 978-991.[引用本文:1] |
| [6] | Hossain A, Biswas P K, Chakrabarti S. Sensing models and its impact on network coverage in wireless sensor network[C]// IEEE Region 10 and 3rd International Conference on Industrial and Information Systems(ICIIS 2008).India: IEEE Press, 2008: 1-5.[引用本文:1] |
| [7] | Yu Jiguo, Ren Shaohua, Wan Shengli, et al. A stochastic k-coverage scheduling algorithm in wireless sensor networks [J]. International Journal of Distributed Sensor Networks, 2012, 33(5): 26-38.[引用本文:1] |
| [8] | Ammari H M, Das S K. Centralized and clustered k-coverage protocols for wireless sensor networks [J]. IEEE Transactions on Computers, 2012, 61: 118-133.[引用本文:1] |