2. 特殊环境机器人技术四川省重点实验室, 四川 绵阳 621010;
3. 清华大学 电子工程系, 北京 100084
为了刻画网络冗余流量在小时间尺度下的局部特性,提出了基于柯西-拉普拉斯多分形小波模型及其参数估计算法. 采用联合分布函数来描述冗余流量的局部表征,即分别用柯西分布和拉普拉斯分布计算冗余流量的重尾和尖峰参数乘法因子;通过概率比较方法获取小波系数和尺度系数的比例参数阈值,以界定两种不同分布的参数范围. 实验结果表明,提出的模型能准确且有效地描述网络冗余流量在小时间尺度下的多分形特性.
2. Robot Technology Used for Special Environment Key Laboratory of Sichuan Province, Sichuan Mianyang 621010, China;
3. Department of Electronic Engineering, Tsinghua University, Beijing 100084, China
In order to characterize local features of network redundant traffic on small-time scale more accurately, a new Cauchy-Laplace multifractal wavelet model was proposed. An algorithm for estimating parameters of wavelets was also put forward. A joint distribution function was adopted to describe local features, i.e., Cauchy and Laplace distributions were used to obtain the parameter multiply factors for heavy-tailed and spike features, respectively. A threshold for ratio of wavelets to scaling parameters, which decides how these two distributions affected redundant traffic modeling, was achieved by probability comparison. Experiments show that the proposed model can well characterize small-time scale multifractal features of network redundant traffic.
互联网中冗余流量的存在极大地降低了网络通信的有效性[1]. 目前,已有一些针对网络冗余流量消除算法的研究[2, 3],但对于真实网络中冗余流量的特性分布与复杂网络建模的研究,仍处于起步阶段. 实际中的网络流量呈现出明显的尺度特性,多分形小波建模(MWM,multifractal wavelet model)方法则能较好地模拟网络流量中的多分形特征[4].
通过对冗余流量的实测,发现其呈现出明显的尖峰和重尾特性,而已有的MWM并不能很好地描述这一双重特性. 笔者通过柯西-拉普拉斯多分形小波模型(CLMWM,Cauchy-Laplace multifractal wavelet model)实现更为准确地描述真实网络中冗余流量的小时间尺度下的局部特性.
1 网络冗余流量的特性分析 1.1 冗余流量的自相似性网络冗余流量的自相似性表现在大范围的时间尺度上具有相似的强突发性,与传统泊松分布的缓和性质完全不同. 流量序列的自相似程度用Hurst参数(用H表示)来衡量,并使用R/S分析法来验证冗余流量是否较传统网络流量具有更强的自相似性.
对网络流量以及网络冗余流量分别绘制了R/S点图,两条拟合曲线的斜率分别为0.633 3和 0.733 3. 冗余流量的H值比相对应的网络流量H值大,说明冗余流量比一般网络流量具有更强的自相似特性.
1.2 冗余流量的重尾分布特性冗余流量的自相似性与重尾分布之间有着紧密的联系,根据特征指数来验证流量数据包序列的统计指标是否和Alpha稳定分布相一致,特征指数的大小直接反映了分布的重尾程度. 实验验证网络流量和网络冗余流量的特征值分别是1.253 7和1.186 2,可见,冗余流量的特征指数值比相应的网络流量的特征指数值要小,而特征指数值越小,表明概率密度曲线的尖峰越强,分布的尾部越重. 同时发现,网络冗余流量较相应的网络流量,具有更强的尖峰和重尾特性.
2 CLMWM 2.1 MWMMWM的主要思想:首先对流量分布特性用时间序列进行表述,然后采用具有对称分布特点的β分布得到尺度和小波系数的比值,最后采用小波重构算法生成网络模拟流量. 但在对网络流量进行建模时,需对小波模型的小波系数和尺度系数加以约束,以使得网络流量的特性更加符合实际情况.
MWM采用Haar小波分析,它的尺度函数φ(x)表示为
| $\varphi \left( x \right)=\left\{ \begin{align} & 1,\ \ \ \ \ 0\le x < 2 \\ & 0,\ \ \ \ \ 其他 \\ \end{align} \right.$ | (1) |
小波函数ψ(x)与尺度函数φ(x)的关系为
| $\Psi \left( x \right)=\varphi \left( 2x \right)-\varphi \left( 2x-1 \right)$ | (2) |
则对于信号X(t),尺度系数Uj,k和小波系数Wj,k分别可以表示为
| ${{U}_{j,k}}=\int{X\left( t \right)}{{\varphi }_{j,k}}\left( t \right)dt$ | (3) |
| ${{W}_{j,k}}=\int{X\left( t \right)}{{\Psi }_{j,k}}\left( t \right)dt$ | (4) |
其中:j=0,1,2,…,n为尺度,k为不同的移位位置. j=0表示最粗的尺度,此时其分辨度是最低的;j=n表示最细的尺度,此时分辨度最高.
| ${{\varphi }_{j,k}}\left( t \right)={{2}^{j/2}}\varphi \left( {{2}^{j}}-k \right)$ | (5) |
| ${{\Psi }_{j,k}}\left( t \right)={{2}^{j/2}}\Psi \left( {{2}^{j}}-k \right),j,k\in Z$ | (6) |
因为网络流量中的一维时间序列X(t)是非负的,则对任意j、k而言,不同尺度情况下的均值Uj,k也是非负的. 由Haar尺度和小波系数的逆变换可推出约束条件为|Wj,k|≤Uj,k.
因此可定义:
| ${{W}_{j,k}}={{A}_{j,k}}{{U}_{j,k}}$ | (7) |
其中Aj,k为在[0, 1]区间上的随机变量.
为了方便进行排队分析,选择β分布进行建模,依据β分布可得到尺度系数的初值,然后经过迭代得到Harr小波变换各层的尺度和小波系数,最后根据式(8)得到网络流量.
| $X\left( t \right)=\sum\limits_{k}{{{U}_{j,k}}{{\varphi }_{j,k}}}\left( t \right)+\sum\limits_{j=0}^{\infty }{{{W}_{j,k}}{{\Psi }_{j,k}}\left( t \right)}$ | (8) |
真实的网络冗余流量具有尖峰特性和重尾分布特性,所以传统的MWM不能有效地描述流量特性. 为此,在迭代构造小波系数和尺度系数时,分别选取了柯西分布、高斯分布以及拉普拉斯分布.
2.2 CLMWM的参数估计在现有的MWM中,都是采用单一的统计分布来刻画网络流量特性,而真实的网络冗余流量具有双重特性,因此采用一种联合分布方式即柯西-拉普拉斯分布来对冗余流量的特性进行描述.
CLMWM进行模型构建时,关键的地方在于计算比例系数Aj,k. 由于采用柯西分布和拉普拉斯分布共同来确定比例系数Aj,k,因此在CLMWM中,比例系数Aj,k被分成两部分,在某个分类范围内比例系数Aj,k由拉普拉斯分布来确定,而其他范围由柯西分布来确定. 同时,需要求出分类阈值T,这样就能很好地得到分类范围.
对于冗余流量数据序列X(t),可以看作是在有限时间[0,N]上采样得到的离散序列X(n)[k],离散序列X(n)[k]的分辨率为b-n(b、n为正整数且b≥2). 在多分形谱的计算中,分辨度n的值越大,多分形谱的计算精度越高,但是,分辨度n过大,又会极大地提高多分形谱的计算复杂度,所以,n通常取10~20之间的值. 本节n取值为15,冗余流量的序列长度N取值为1,在序列长度较小的情况下,参数b通常取值为2.
1) 拉普拉斯分布的参数估计
拉普拉斯分布的概率密度分布函数f(x)为
| $f\left( x \right)=\frac{1}{2b}\exp \left( -\frac{\left| x-\mu \right|}{b} \right)$ | (9) |
其中:μ为位置参数,b为尺度参数. 尺度参数b可以通过最大似然估计法来确定.
2) 柯西分布的参数估计
柯西分布的概率密度函数g(x)可以表示为
| $g\left( x \right)=\frac{1}{\pi }\left[\frac{\gamma }{{{\left( x-\mu \right)}^{2}}+{{\gamma }^{2}}} \right]$ | (10) |
其中:μ为位置参数,γ为尺度参数. 尺度参数γ同样由最大似然估计法来确定.
3) 分类阈值T
这里拉普拉斯分布和柯西分布的位置参数μ=0.5,因此T-0.5关于原点对称. 设PC(T)为柯西分布概率密度在[-∞,-T+0.5)和(T-0.5,∞] 区间内的积分值,其计算式为
| $int{_{-\infty }^{-T+0.5}}\frac{1}{\pi }\frac{\gamma }{{{\left( x-0.5 \right)}^{2}}+{{\gamma }^{2}}}dx$ | (11) |
设PL(T)为拉普拉斯分布概率密度在[-T+0.5,T-0.5]区间内的积分值,其计算式为
| $\begin{align} & {{\text{P}}_{\text{L}}}\text{(T)=P(-T+0}\text{.5}\le x\le T-0.5)= \\ & \int{_{-T+0.5}^{-T-0.5}}\frac{1}{2b}\exp \left( -\frac{\left| x-0.5 \right|}{b} \right)dx \\ \end{align}$ | (12) |
令PC(T)=PL(T),由式(11)和式(12)就可求出分类阈值T. 因此,在CLMWM中比例系数Aj,k的确定方式:当|x|≤T-0.5时,比例系数Aj,k由拉普拉斯分布确定;当|x|>T-0.5时,比例系数Aj,k由柯西分布确定.
3 实验及分析 3.1 实验数据集所用的网络流量数据取自WIDE项目组中F采样点收集的数据,F采样点位于一条带宽为150 Mbit/s的环太平洋链路上,数据编号为201210011400,大小为2 698.36 MB. 小时间尺度上到达的数据包个数比较少,甚至有些时间间隔内没有数据包到达,所以先对数据进行预处理后而得到网络冗余流量. 以0.1 s为间隔,只取前215个数据.
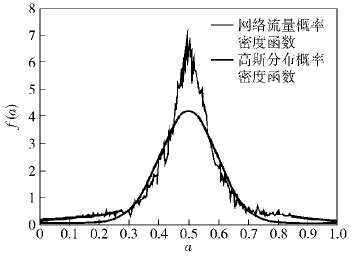
3.2 实验分析实验分别选取高斯分布、拉普拉斯分布、柯西分布以及柯西-拉普拉斯分布作为乘法因子的CLMWM对冗余流量数据进行聚合,得到每一层的数据,因为共有215个数据,所以数据共有15层. 考虑篇幅紧凑性,仅给出了第3层的概率密度分布和拟合分布曲线,如图 1~图 4所示.
由图 1可知,MWM是采用高斯分布作为乘法因子的模型,在描述冗余流量的尖峰和重尾分布特性时,都不能很好地与第3层的流量概率密度分布相拟合. 该方法是上述几个模型中对冗余流量拟合效果最差的.
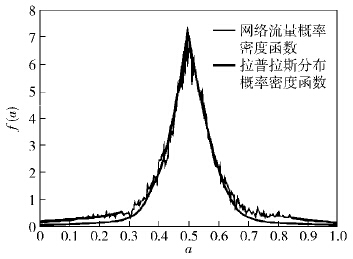
考虑篇幅紧凑性,仅给出了第3层的概率密度分布和拟合分布曲线,如图 2是采用拉普拉斯分布作为乘法因子的MWM得出的冗余流量概率密度分布,该分布很好地拟合了冗余流量的概率密度尖峰特性,但不能准确地描述冗余流量的重尾特性.
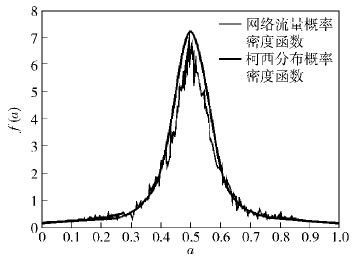
考虑篇幅紧凑性,仅给出了第3层的概率密度分布和拟合分布曲线,如图 3采用的是柯西分布作为乘法因子的MWM. 柯西分布的尾部衰减比较慢,具有重尾特性,更能准确地描述网络流量的尾部形态. 但是,在描绘冗余流量尖峰特性上,柯西分布不如拉普拉斯分布.
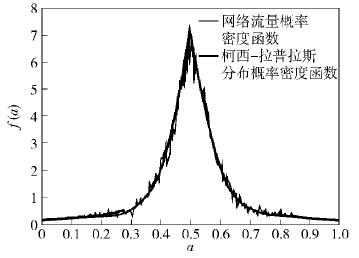
考虑篇幅紧凑性,仅给出了第3层的概率密度分布和拟合分布曲线,如图 4采用的是柯西-拉普拉斯分布作为乘法因子的混合分布MWM. 该模型无论在描述冗余流量的概率密度尖峰特性,还是描述其重尾分布特性上,都有很好的拟合效果. 在CLMWM中,拉普拉斯分布在[0.4,0.6]内能很好地拟合冗余流量的尖峰特性,而在[0,0.4)和(0.6,1]的范围内,柯西分布很好地刻画了冗余流量的重尾分布特性.
4 结束语提出了一种以联合分布函数作为乘法因子的MWM,即CLMWM. 通过实验验证了网络冗余流量存在的自相似,以及更为突出的尖峰和重尾特性. 在CLMWM中,比例系数被分类阈值分成两部分,重尾部分的比例系数由柯西分布来描述,尖峰部分的比例系数由拉普拉斯分布来描述. 实验结果表明,与其他MWM相比,CLMWM能更有效刻画小时间尺度下的冗余流量双重特性.
| [1] | 张宾,杨家海,吴建平. Internet流量模型分析与评述[J]. 软件学报, 2011, 22(1): 115-131. Zhang Bin, Yang Jiahai, Wu Jianping. Survey and analysis on the Internet traffic model[J]. Journal of Software, 2011, 22(1): 115-131.[引用本文:1] |
| [2] | 郑鸿,邢玲,马强. 基于分组特性的冗余流量消除算法[J]. 计算机应用,2014, 34(6):1541-1545. Zheng Hong, Xing Ling, Ma Qiang. Redundancy traffic elimination algorithm based on packet feature[J]. Journal of Computer Application, 2014, 34(6):1541-1545.[引用本文:1] |
| [3] | 刘珍,王若愚,刘琼. 基于Bootstrapping的英特网流量分类方法[J]. 北京邮电大学学报, 2014, 37(5): 66-70. Liu Zhen, Wang Ruoyu, Liu Qiong. Study of Internet traffic classification method based on Bootstrapping[J]. Journal of Beijing University of Posts and Telecommunications, 2014, 37(5): 66-70.[引用本文:1] |
| [4] | Julio C, Ramirez Racheco, Deni Torres Roman. A tool for long-range dependent analysis via the R/S statistic[C]// 2006 International Conference on Communications (ICC2006).Mexico City: IEEE Press, 2006: 361-366.[引用本文:1] |