提出一种蜂窝与终端自组织混合网络中多跳直通通信的路由选择方法. 首先给出混合网络下的多跳直通通信的干扰模型和信道模型,并考虑了蜂窝终端对直通通信终端的干扰范围. 基于模型分析并得到D2D通信下的中断概率公式,然后将此公式应用在多跳路由选择中,提出了一种多跳路由选择方法. 仿真结果表明,与其他路由算法比较,新提出的方法可以有效提高吞吐量.
A multi-hop route selection of device-to-device (D2D) communication in cellular and Ad hoc hybrid networks was proposed. Interference model and channel model of multi-hop D2D communication were given, and the interference range from cellular user equipment (UE) to D2D UE was considered as well. Based on the model, the formula of outage probability in D2D communication was analyzed and obtained. The formula was applied into the multi-hop route selection, and then one solution of multi-hop route selection was proposed. Simulation shows the proposed solution can improve the capacity.
近年来,局部热点区域对高速率日益增长的需求使蜂窝网络下的终端直通通信成为研究热点.蜂窝与终端直通通信混合网络作为一种特殊的认知无线电网络,路由选择是一个基本的研究问题[1].
Ghasemi等[2]建议使用相同的优化策略使遍历容量达到最大. Lee等[3]给出平坦瑞利衰落信道下目的终端的SINR闭式概率密度函数(PDF,probability density function)和累积分布函数(CDF,cumulative distribution function)表达式,并就最大遍历容量和中断概率研究端到端的性能. Ma等[4]使用跳数来衡量路由性能. 像Boyer等[5]那样,笔者考虑多跳直通通信,并使路由跳数最少. 在本研究中,根据混合网络下的多跳直通通信的场景假设和信道模型,分析并计算得到直通通信中断概率的表达式. 然后将得到的中断概率表达式应用到多跳直通路由选择方案中,给出了多跳路由选择方法.
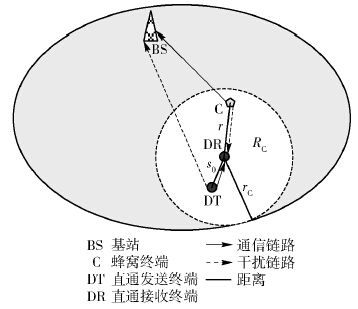
1 干扰模型和SINR分析 1.1 干扰模型图 1给出了干扰模型,其中DT是直通通信的发送终端,DR是直通通信的接收终端. C是蜂窝终端,其上行链路资源被DT到DR的直通通信复用. 假设以DR为圆心,rC为半径的区域内被DT复用资源的蜂窝终端会对DR造成干扰,将此区域定义为RC. 蜂窝上行通信的接收端(基站)会受到来自DT的干扰. 在这里,只考虑一对源终端和目的终端之间的多跳通信,且直通通信距离基站较远,每一跳直通通信都是在不同的时刻完成的,从而不会对基站造成累积干扰. r是C到DR的距离,假设r在区域RC中服从均匀分布[6];s0是DT和DR之间的距离,并且是已知的.
1.2 信道模型设蜂窝与终端自组织混合网络中,信道服从瑞利衰落模型. 对于距离为d的发送端和接收端,接收端的接收功率Pr为
| \[{P_r} = {P_0}{\left( {d/{d_0}} \right)^{ - n}}\xi ,d \ge {d_0}\] | (1) |
根据信道模型,设终端直通通信的发射功率为PDT,蜂窝通信的发射功率为PC. 考虑DT和DR之间的直通通信与C到基站的蜂窝通信,在区域RC中的被直通通信复用上行链路资源的蜂窝终端C会对直通通信接收终端DR造成干扰. 假设它们发射端的天线增益与接收端的天线增益相同,且都工作在波长为l的频段上,则在DR处的接收功率为${P_{{\rm{DR}}}} = {P_{{\rm{DT}}}}c{\left( {{s_0}/{d_0}} \right)^{ - n}}{\xi _1}$,在DR处受到的干扰为${I_{{\rm{DR}}}} = {P_{\rm{C}}}c{\left( {r/{d_0}} \right)^{ - n}}{\xi _2}$,其中${s_0} \ge {d_0},r \ge {d_0},c = {G_t}{G_r}{l^2}{\left( {4\pi {d_0}} \right)^2}$.
假设噪声功率$N \ll {I_{{\rm{DR}}}}$,则DT和DR之间直通通信的信号和干扰加噪声比(SINR,signal to interference plus noise ratio)可由式(2)计算得到
| \[\frac{{{P_{{\rm{DR}}}}}}{{{I_{{\rm{DR}}}}}} = \frac{{{P_{{\rm{DT}}}}c{{\left( {{s_0}/{d_0}} \right)}^{ - n}}{\xi _1}}}{{{P_{\rm{C}}}c{{\left( {r/{d_0}} \right)}^{ - n}}{\xi _2}}} = \frac{{{P_{{\rm{DT}}}}}}{{{P_{\rm{C}}}}}{\left( {\frac{{{s_0}}}{r}} \right)^{ - n}}\frac{{{\xi _1}}}{{{\xi _2}}}\] | (2) |
设DT和DR之间直通通信的SINR为γ,则DT和DR之间直通通信的中断概率为
| \[{P_{{\rm{out}}}} = \Pr \left\{ {\gamma \lt {\gamma _0}} \right\} = \int\limits_0^{{\gamma _0}} {{f_\gamma }\left( \gamma \right){\rm{d}}\gamma } \] | (3) |
基于1.1节,因为C到DR的距离r在区域RC中服从均匀分布(即C落入在RC圆区域任意点上的概率是等同的),则r的PDF为
| \[{f_{\rm{R}}}\left( r \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{{2r}}{{{r_{\rm{C}}}}},r \le {r_{\rm{C}}}}\\ {0,其他 } \end{array}} \right.\] | (4) |
设DT和DR之间直通通信服从瑞利衰落信道,ξ1服从指数分布,即ξ1的PDF为
| \[f\left( {{\xi _1}} \right) = \left\{ {\begin{array}{*{20}{l}} {{\lambda _1}{\rm e^{ - {\lambda _1}{\xi _1}}},{\xi _1} \gt 0}\\ {0,{\xi _1} \le 0} \end{array}} \right.\] | (5) |
类似地,在C和DR之间的干扰链路中,ξ2服从指数分布,可以得到ξ2的PDF.
令T=R/s0,U=Tn,已知DT和DR之间的距离s0,则随机遍历U为
| \[{f_{\rm{U}}}\left( u \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{{s_0^2{\mu ^{\frac{1}{n} - 1}}}}{{r_{\rm{C}}^2}},0 \lt u \le {{\left( {\frac{{{r_{\rm{C}}}}}{{{s_0}}}} \right)}^n}}\\ {0,其他 } \end{array}} \right.\] | (6) |
令v=ξ1/ξ2,V=Ξ1/Ξ2,当2个随机变量X、Y相互独立时,随机变量V的PDF为
| \[{f_{\rm{V}}}\left( v \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{{{\lambda _1}{\lambda _2}}}{{{{\left( {{\lambda _1}v + {\lambda _2}} \right)}^2}}},v \ge 0}\\ {0,其他 } \end{array}} \right.\] | (7) |
令Q=UV,则
| \[\begin{array}{*{20}{c}} {P\left\{ {Q \le q} \right\} = \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{\frac{q}{u}} {f\left( {u,v} \right)} } {\rm{d}}u{\rm{d}}v = }\\ {\int\limits_0^B {f\left( u \right)} {\rm{d}}u\int\limits_0^{\frac{q}{u}} {f\left( v \right)} {\rm{d}}v = \frac{{2s_0^2}}{{r_{\rm{C}}^2}}\sqrt {\frac{{{\lambda _1}q}}{{{\lambda _2}}}} \arctan \left( {\frac{{r_{\rm{C}}^2}}{{s_0^2}}\sqrt {\frac{{{\lambda _2}}}{{{\lambda _1}q}}} } \right)} \end{array}\] | (8) |
| \[\begin{array}{*{20}{c}} {{P_{{\rm{out}}}} = \Pr \left\{ {\gamma {\rm{ \lt }}{\gamma _0}} \right\} = \Pr \left\{ {\frac{{{P_{{\rm{DT}}}}}}{{{P_{\rm{C}}}}}q{\rm{ \lt }}{\gamma _0}} \right\} = \Pr \left\{ {q{\rm{ \lt }}\frac{{{\gamma _0}{P_{\rm{C}}}}}{{{P_{{\rm{DT}}}}}}} \right\} = }\\ {\frac{{2s_0^2}}{{r_{\rm{C}}^2}}\sqrt {\frac{{{\lambda _1}{\gamma _0}{P_{\rm{C}}}}}{{{\lambda _2}{P_{{\rm{DT}}}}}}} \arctan \left( {\frac{{r_{\rm{C}}^2}}{{s_0^2}}\sqrt {\frac{{{\lambda _2}{P_{{\rm{DT}}}}}}{{{\lambda _1}{\gamma _0}{P_{\rm{C}}}}}} } \right)} \end{array}\] | (9) |
由式(10)可知,当已知直通通信发送端和接收端之间的距离s0时,假设系统参数λ1、λ2、γ0已知,令$a = \sqrt {{\lambda _2}/{\lambda _1}{\gamma _0}} /s_0^2,x = r_{\rm{C}}^2\sqrt {{P_{{\rm{DT}}}}/{P_{\rm{C}}}} ,y = ax\left( {x > 0,y > 0} \right)$,则${P_{{\rm{out}}}} = \frac{2}{y}\arctan \left( y \right)$. 若令${P_{{\rm{out}}}} = \beta \left( {0 \le \beta \le 1} \right),g\left( y \right) = \arctan \left( y \right),h\left( y \right) = \frac{\beta }{2}y$ 通过画图可知,当y>0,0≤β≤1时,g(y)和h(y)在第1象限总有1个交点,并且y随着β的减小而增大. 特别地,当β=1时,通过计算可以得到数值解y≈2.331 1;当${{P_{{\rm{out}}}} \to 0}$时,${y \to \infty }$. 令m=2.331 1,从而有
| \[r_{\rm{C}}^2\sqrt {{P_{{\rm{DT}}}}/{P_{\rm{C}}}} \ge ms_0^2\sqrt {{\lambda _1}{\gamma _0}/{\lambda _2}} \] | (10) |
从而,终端直通通信的中断概率Pout与干扰半径rC、蜂窝终端以及直通通信发送终端的发射功率(分别为PC和PDT)有关. 式(10)中,rC、PC和PDT为变量. 在进行终端直通通信时,干扰半径越大,直通终端发射功率越大,并且蜂窝终端发射功率越小,直通通信越可能正常进行.
3 多跳直通通信的路由选择方案假设在终端直通通信时,直通通信发送终端复用的是距离直通通信接收终端最远的蜂窝终端的上行链路资源. 假设直通通信的中断概率门限值为η. 当Pout≤η时,2个终端之间可进行一跳直通通信;当Pout>η时,则通过中继终端进行多跳直通通信.
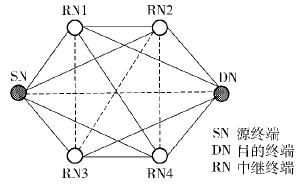
如图 2所示,图G中SN为直通通信的源终端,DN为直通通信的目的终端,RN为直通通信的中继终端. 各终端在图 2中表示成顶点,用实线表示的边代表 2个终端之间可以进行通信,且边的权值为直通通信的中断概率;用虚线表示的边代表 2个终端之间需要通过多跳的方式进行直通通信. 图G实际上为有向图. 在这里,为降低算法的复杂度,将有向图转化为无向图. 选择在原有向图中1对有向边权值中的较大值作为相应的无向图边的权值.
3.1 基于最小生成树的路由选择方案最小生成树路由选择(minimum spanning tree route selection)算法是在描述终端以及终端之间直通通信的中断概率情况的图G中,首先判断图G是否为连通图. 若为连通图,则选出最小生成树,并且端到端在最小生成树上的路径就是其路由;否则不存在多跳直通路由.
由于端到端的多跳直通通信的信道容量不仅与中断概率有关,而且与路径中的跳数有关,即
| \[C = \frac{1}{k}\left( {1 - \max \left\{ {P_{{\rm{out}}}^i} \right\}} \right){\rm{lb}}\left( {1 + {\gamma _0}} \right)\] | (11) |
根据基于最小生成树的改进路由选择(modified route selection)算法,得到的源终端到目的终端的路径L为最佳路由. 算法如下.
1 初始化
2 G={V,E},其中V为顶点的集合,E为边的集合. |V|≥2表示顶点个数,|E|表示边的数目. 集合V中的顶点按照度数由小到大依次排序V={v1,v2,…,vN},其中N=|V|,表示源终端的顶点记为vk,表示目的终端的顶点记为vm. 集合V1=$\emptyset $,E1=$\emptyset $,E2=$\emptyset $.
3 步骤1 判断是否为连通图
4 while V{vk,vm}
5 if|E|<|V|-1
6 V=V-{vi} (i=1,…,N,i≠k,i≠m)E=E-{e1,…,ej},其中e1,…,ej为与vi相连的边,j为vi的度数,转至步骤1;
7 else
8 G={V,E}为连通图,|V|=N′,|E|=M′,转至步骤2;
9 步骤2 最小生成树Kruskal算法
10 if E≠$\emptyset $
11 while w(ei)=min{w(e1),w(e2),…,w(e|E|)}且E1=E1+{ei}无圈
12 E1=E1+{ei},E=E-{ei},转至步骤2;
13 else
14 得到最小生成树T={V1,E1}以及源终端与目的终端之间的路径L,转至步骤3;
15 步骤3
16 if E-E1∪E2≠$\emptyset $
17 选择e′i,e′i∈E-E1∪E2
18 while e′i(e′i∈E-E1∪E2)与L中的p条边e′1,e′2,…,e′p构成圈(p≤|L|),且$\frac{{1 - \max \left\{ {w\left( L \right),w\left( {e'} \right)} \right\}}}{{\left| L \right| - p + 1}} > \frac{{1 - \max \left\{ {w\left( L \right)} \right\}}}{{\left| L \right|}}$
19 L=L+{e′i}-{e′1,e′2,…,e′p},e1=e1-{e′1,e′2,…,e′p>},e2=e2+{e′1,e′2,…,e′p},转至步骤3;
20 else
21 L即为最佳路由;
22 end
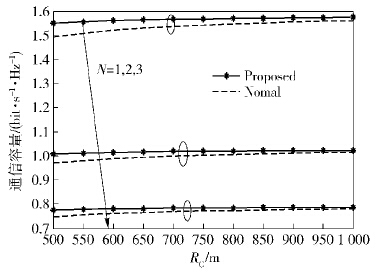
如图 3所示,“*”为由式(9)和式(11)得到的通信容量,将其定义为Proposed;“--”为Lee等[3]计算的通信容量,将其定义为Normal. 分别比较它们在多跳跳数N分别为1,2,3时的2种通信容量. 设终端单跳的距离s0=40 m,PC/PD=1. 从图 3中可以看出,通信容量随着干扰距离的增大而逐渐增大,随着跳数的增加而减小. 使用笔者提出的方法得到的通信容量要优于Lee等[3]计算的通信容量.
4.2 路由算法仿真和分析在路由算法的仿真中,设中断概率门限η=0.05. 直通通信发送终端复用距离直通通信接收终端最远的蜂窝终端的上行链路资源,并且设此蜂窝终端的发射功率为最大发射功率Pmax. 根据式(9)可知,若使直通通信的中断概率最小,则直通通信发送终端的发射功率也应为Pmax.
从式(11)可以看出,信道容量受到中断概率和跳数2个方面的影响. 当1跳直通通信的中断概率小于中断门限时,跳数的影响可能占主要地位. 因此,可以比较最小跳数路由算法(min hop route selection)与最小生成树路由选择算法以及改进路由选择算法的性能增益. 在最小跳数路由算法中,由于它基于中断概率门限,因此它和其他2种路由算法都基于相同的中断概率邻接矩阵.
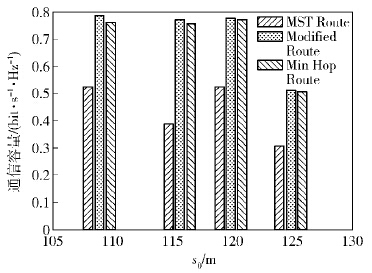
在仿真中,设终端数目M=152. 终端分布服从均匀分布. 随机得到的多跳直通通信的源终端与目的终端之间的距离DSN-DN分别为108.90 m、115.62 m、119.86 m以及124.88 m. 依据式(9)和式(11)计算中断概率,并得到中断概率邻接矩阵. 根据邻接矩阵,可以得到终端之间不同距离下的最小生成树. 图 4给出了3种路由选择方案在通信容量上的增益对比. 基于相同的中断概率邻接矩阵,相比基于最小生成树的方案,改进的路由选择方案可以获得更高的信道容量. 相比最小跳数路由方案,因为改进的路由算法考虑了中断概率对通信容量的影响,因此可以获得比最小跳数方案更大的通信容量,并且可以得到与最小跳数方案相同的路径跳数.
由于仿真时撒点是随机的,不同的源终端与目的终端之间的距离所得到的路由选择结果不同,不同终端距离之间使用不同路由选择算法时获得的信道容量不具有可比性. 图 4只用于说明在源终端与目的终端之间的距离相同时,改进的路由选择方案相比基于最小生成树的方案以及最小跳数路由方案,可以获得更高的信道容量.
5 结束语给出混合网络下多跳直通通信的干扰模型以及信道模型,考虑蜂窝通信终端对直通通信终端的干扰范围. 分析计算得到直通通信中断概率的表达式,并将其应用到多跳直通路由选择方案中,提出最小生成树路由选择改进方案. 仿真结果表明,提出的路由选择方案在通信容量上优于基于最小生成树路由算法以及最小跳数路由算法.
| [1] | Sengupta S, Subbalakshmi K P. Open research issues in multi-hop cognitive radio networks[J]. IEEE Communications Magazine, 2013, 51(4): 168-176.([引用本文:1]) |
| [2] | Ghasemi A, Sousa E S. Fundamental limits of spectrum-sharing in fasing environments[J]. IEEE Trans Wirless Commun, 2007, 6(2): 649-658.([引用本文:1]) |
| [3] | Lee D, Kim S I, Lee J, et al. Performance of multi-hop decode-and-forward relaying assisted device-to-device communication underlaying cellular networks[C]//Honolulu. Hawaii, USA: International Symposium on Information Theory and Its Applications(ISITA), 2012: 455-459.([引用本文:3]) |
| [4] | Ma M, Tsanga D H K. Joint design of spectrum sharing and routing with channel heterogeneity in cognitive radio networks[J]. Physical Communication, 2009, 2(1-2): 127-137.([引用本文:1]) |
| [5] | Boyer J, Falconer D D, Yanikomeroglu H. Multihop diversity in wireless relaying channels[J]. IEEE Trans Wireless Commun, 2004, 52(10): 1820-1830.([引用本文:1]) |
| [6] | Salameh, et al. Mac protocol for opportunistic cognitive radio networks with soft guarantees[J]. IEEE Transactions on Mobile Computing, 2009, 8(10): 1339-1352.([引用本文:1]) |
| [7] | Rappaport T S. Wireless communication-principles and practice[M]. 2ed. USA : Prentice-Hall Press, 2001.([引用本文:1]) |