2. 宽带无线通信与传感网技术教育部重点实验室(南京邮电大学), 南京 210013
提出了一种用于两层传感网的基于桶划分的隐私保护Top-k查询处理(BPTQ)方法. BPTQ通过引入桶划分策略和加密技术,能够确保感知数据在存储、通信及查询处理过程中的隐私安全性. 理论分析和实验结果表明,该方法能够保护感知数据的隐私安全,且与现有方法相比具有更高的能耗效率.
2. Key Laboratory of Broadband Wireless Communication and Sensor Network Technology (Nanjing University of Posts and Communications), Ministry of Education, Nanjing 210023, China
A bucket partition based privacy-preserving top-k query processing (BPTQ) in two-tiered wireless sensor networks was proposed. BPTQ can protect the privacy of sensing data during the storage, communication and query processing by introducing bucket partitioning scheme and encryption technique. Analysis and experiments show that BPTQ can preserve the privacy of the sensing data and query result, and it is more efficient in energy consumption than the existing work.
两层传感器网络在传统多跳传感器网络的基础上引入了作为中间层的存储节点,具有网络拓扑简单、易于扩展、查询效率高等优点,有良好的发展前景[1].
在两层传感器网络中,感知数据的安全问题十分突出,安全Top-k查询处理技术[2, 3, 4, 5]已经引起了越来越多的关注. 笔者将桶划分技术[6]和对称加密技术用于Top-k查询处理,提出了一种基于桶划分的隐私保护Top-k查询处理(BPTQ,bucket partition based privacy-preserving top-k query processing)方法,并通过仿真实验分析了感知节点网内通信代价以及存储节点与基站之间的通信代价.
1 模型与问题描述 1.1 网络模型采用Gnawali等[1]提出的两层传感器网络模型:整个无线传感网络分割为若干个单元,每个单元由1个存储节点SM和n个感知节点{s1,s2,…,sn}组成.
假设在每个时间周期t内,感知节点si(i=1,2,…,n)采集N个感知数据,记为Di={di,1,di,2,…,di,N},不妨设di,1>di,2>…>di,N. 对于非数值型的感知数据,可以利用公有评分函数[7]计算出其对应的得分数值,即将其转换为可进行比较的数值型数据.
1.2 威胁模型与问题描述网络安全模型采用“honest-but-curious”威胁模型[8],即假设感知节点和基站可信,而存储节点不可信,存储节点有窥探其他节点数据隐私的企图,但仍然遵循查询协议执行命令.
在两层传感器网络中,由于SM存储着所有的感知数据,而且要执行基站的查询指令,一旦被俘获,将影响整个网络的隐私安全. 基于此,重点关注由于SM被俘获而造成的数据隐私泄露问题.
2 基于桶划分的隐私保护Top-k查询 2.1 桶划分机制Hacigumus等[6]首次提出桶划分技术,并用于数据库安全查询.
定义1 桶划分:将数据域[A,B]划分为n个连续且不重叠的区间[a1,a2),[a2,a3),…,[an,an+1],满足
| \[\begin{array}{*{20}{l}} {\left[ {{a_1},{a_2}} \right) \cup \left[ {{a_2},{a_3}} \right) \cup \cdots \cup \left[ {{a_n},{a_{n + 1}}} \right] = \left[ {A,B} \right]}\\ {\forall i,j \in \left\{ {1,2, \cdots ,n} \right\} \wedge i \ne j \to \left[ {{a_i},{a_{i + 1}}} \right) \cap \left[ {{a_j},{a_{j + 1}}} \right) = \emptyset } \end{array}\] |
其中:任意区间[ai, ai+1)即为“桶”,A和B是数据域的上下边界.
定义2 桶标签:对于定义1中的任意区间[ai,ai+1),存在映射关系F,即
| \[F:\left[ {{a_i},{a_{i + 1}}} \right) \to {T_i},i \in \left\{ {1,2, \cdots ,n} \right\},{T_i} \in {N_ + }\] |
定义3 在相同的桶划分中,设有桶标签Ti和Tj,则Ti和Tj对应的区间$T_i^*$和$T_j^*$必定具有下列关系之一.
1) $T_i^ * \gt T_j^ * $:满足$\forall {d_i} \in T_i^ * ,{d_j} \in T_j^ * \to {d_i} \gt {d_j}$;
2) $T_i^ * \lt T_j^ * $;满足$\forall {d_i} \in T_i^ * ,{d_j} \in T_j^ * \to {d_i} \lt {d_j}$;
3) $T_i^* = T_j^*$:满足Ti=Tj,即Ti和Tj为同一区间的标签.
2.2 BPTQ假设感知数据的取值范围划分为m个桶,记为集合TAG={T1,T2,…,Tm},不妨设T1,T2,…,Tm满足T1*>T2*>…>Tm*. 为了便于描述,对相关符号进行定义,如表 1所示.
|
|
表 1 符号定义 |
在感知数据上传阶段,感知节点在单位时间周期内完成数据采集后,将采集到的感知数据按桶进行划分,并加密桶数据,然后将相关数据上传至SM进行存储. 具体处理过程如协议1所示.
协议1 感知数据上传协议
1) si在t内采集到N个数据,记为集合Di={di,1,di,2,…,di,N};根据预定的桶划分策略,假设这N个数据分布在wi(wi≤m,m表示总的分桶数量)个桶内,其标签设为Ti,1,Ti,2,…,Ti,wi;设Ti,j桶内包含μi,j(μi,j>0)个感知数据,记为集合Di,j,显然$\sum\limits_{j = 1}^{{w_i}} {{\mu _{i,j}}} = N,\bigcup\limits_{j = 1}^{{w_i}} {{D_{i,j}} = {D_i}} $.
si对每个非空桶内的数据集合利用密钥Ki进行加密处理,并按照如下格式构造数据消息上传给SM.
| \[{s_i} \to {S_M}\left\langle {i,t,{T_{i,1}},{\mu _{i,1}},{{\left( {{D_{i,1}}} \right)}_{{K_i}}}, \cdots ,{T_{i,{w_i}}},{\mu _{i,{w_i}}},{{\left( {{D_{i,{w_i}}}} \right)}_{{K_i}}}} \right\rangle \] |
2) SM接收完本单元内所有感知节点上传的数据消息后,根据标签信息对相同桶内的密文数据集进行归类,并统计归类后各桶内数据的总数量,然后按如下格式进行存储.
| \[\begin{array}{*{20}{l}} {{S_M}:\left\langle {\begin{array}{*{20}{l}} {t,{T_{{e_1}}},{\mu _{{e_1}}},\left\{ {i,{{\left( {{D_{i,{e_1}}}} \right)}_{{K_i}}}|{D_{i,{e_1}}} \ne \emptyset ,i \in \left\{ {1,2, \cdots ,n} \right\}} \right\}}\\ \cdots \\ {{T_{{e_r}}},{\mu _{{e_r}}},\left\{ {i,{{\left( {{D_{i,{e_r}}}} \right)}_{{K_i}}}|{D_{i,{e_r}}} \ne \emptyset ,i \in \left\{ {1,2, \cdots ,n} \right\}} \right\}} \end{array}} \right\rangle } \end{array}\] |
| \[{\mu _{{e_p}}} = \sum\limits_{i \in \left[ {1,n} \right]} {\left| {{D_{i,{e_p}}}} \right|} ,p \in \left\{ {1,2, \cdots ,n} \right\}\] |
一般而言,$\sum\limits_{p = 1}^r {{\mu _{{e_p}}} \ll k,{{\left( {{D_{i,{e_p}}}} \right)}_{{K_i}}}} $为非空桶Tep内感知数据集的密文.
2.2.2 Top-k查询处理协议基站与SM协作完成查询处理的详细过程如协议2所示.
协议2 查询处理协议
1)基站将所要查询的时间周期t发送给SM,即
| \[{\rm{base}}\;{\rm{station}} \to {S_{\rm{M}}}:\left\langle t \right\rangle \] |
2) SM将t内收到并存储的各非空桶的标签以及各桶内感知数据的数量索引信息上传至基站,即
| \[{S_{\rm{M}}} \to {\rm{base}}\;{\rm{station}}:\left\langle {{T_{{e_1}}},{\mu _{{e_1}}}, \cdots ,{T_{{e_r}}},{\mu _{{e_r}}}} \right\rangle \] |
3) 基站根据已知的桶划分策略,对接收到的$\left\langle {{T_{{e_1}}},{\mu _{{e_1}}}, \cdots ,{T_{{e_r}}},{\mu _{{e_r}}}} \right\rangle $按照桶标签对应区间从大到小顺序关系进行排序,不妨设排序后的结果为$\left\langle {{T_{{f_1}}},{\mu _{{f_1}}}, \cdots ,{T_{{f_r}}},{\mu _{{f_r}}}} \right\rangle $,满足$T_{{f_1}}^ * \gt T_{{f_2}}^ * \gt T_{{f_r}}^ * $. 然后选择前$v$个标签${T_{{f_1}}},{T_{{f_2}}}, \cdots ,{T_{{f_r}}}$,满足
| \[\sum\limits_{i = 1}^v {{\mu _{{f_i}}}} \ge k \wedge \sum\limits_{i = 1}^{v - 1} {{\mu _{{f_i}}}} \lt k\] |
| \[{\rm{base}}\;{\rm{station}} \to {S_{\rm{M}}}\left\langle {{T_{{f_1}}},{T_{{f_2}}}, \cdots ,{T_{{f_v}}}} \right\rangle \] |
4) SM收到基站发来的桶标签$\left\langle {{T_{{f_1}}},{T_{{f_2}}}, \cdots ,{T_{{f_v}}}} \right\rangle $后,将各标签对应的桶内密文数据发送给基站,即
| \[{S_{\rm{M}}} \to {\rm{base}}\;{\rm{station}}:\left\langle {\begin{array}{*{20}{l}} {\left\{ {i,{{\left( {{D_{i,{f_i}}}} \right)}_{{K_i}}}|{D_{i,{f_i}}} \ne \emptyset ,i \in \left\{ {1,2, \cdots ,n} \right\}} \right\}}\\ \cdots \\ {\left\{ {i,{{\left( {{D_{i,{f_v}}}} \right)}_{{K_i}}}|{D_{i,{f_v}}} \ne \emptyset ,i \in \left\{ {1,2, \cdots ,n} \right\}} \right\}} \end{array}} \right\rangle \] |
5) 基站收到SM发送的密文数据后,利用与各感知节点共享的密钥,解密得到感知数据明文,进而最终计算出Top-k查询结果.
3 协议分析由协议1和协议2可知,感知节点上传存储至SM的数据均以加密形式存在,且桶划分策略仅由感知节点和基站共享,因此,协议能够保障感知数据对于SM的隐私安全性.
此外,从感知节点的通信代价Cs,以及SM和基站之间的通信代价CQ角度分析协议的通信代价,相关符号定义如表 2所示.
假设网络中存在n个感知节点,每个感知节点在单位时间周期内采集N个数据,N个感知数据平均分布于α个桶内. 则由协议1可知,每个感知节点需要上传至SM的数据为节点ID、时间周期t、α个桶标签和数量索引信息,以及N个感知数据密文. 因此在数据上传阶段,感知节点的网内通信代价为
| \[{C_s} = n\left( {{l_{id}} + {l_t} + \alpha \left( {{l_T} + {l_q}} \right) + N{l_c}} \right)L\] |
|
|
表 2 能耗分析符号定义 |
由协议2可知,完成一次查询处理所产生的通信代价由如下4次数据通信产生:基站发送时间周期t,SM发送桶标签及各桶内感知数据数量索引信息给基站,基站发送包含查询结果的桶标签给SM,SM上传相应的桶数据密文给基站. 设SM需要上传β个桶的数量索引信息给基站,而Top-k查询结果位于δ个桶内,平均每个桶内包含由λ个感知节点所产生的τ个感知数据密文,则查询处理的通信代价即为
| \[{C_Q} = {l_t} + \beta \left( {{l_T} + {l_q}} \right) + \delta {l_T} + \lambda \left( {{l_{id}} + \tau {l_c}} \right)\] |
通过仿真实验对提出的隐私保护Top-k查询处理方法进行性能评估. 采用与文献[2]中的隐私保护Top-k查询(PPTQ,privacy-preserving top-kquery)方法相同的仿真器实现了BPTQ方法. 由文献[2]的结论可知,PPTQ的能耗效率优于SafeTQ,因此仅进行PPTQ和BPTQ的对比实验. 下面将对比两种方法中感知节点的通信代价Cs和存储节点与基站之间的通信代价CQ. 本节采用随机实验数据集,数据服从均匀分布.
4.1 感知节点通信代价对比实验假设感知数据明文长度为16bit,采用均匀桶划分策略,其他参数初始值设置如表 3所示.
|
|
表 3 实验参数 |
在每组实验中,随机地将感知节点分布在网络覆盖范围内,一共生成10组随机拓扑结构的网络,分别用网络ID标识,最后计算10组网络的平均通信代价.
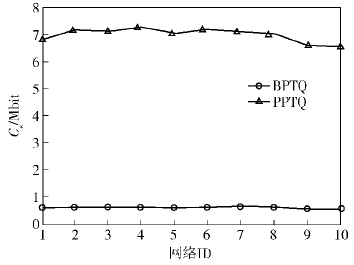
1) 在初始参数条件下,随机生成10组不同拓扑结构的网络,得到在不同网络中的感知节点通信代价如图 1所示. 在不同拓扑结构的网络中,BPTQ和PPTQ的Cs分布情况都较为均匀,但BPTQ产生的Cs显著低于PPTQ. 这是由于在BPTQ中,感知节点上传的数据中桶索引密文长度小于PPTQ中上传的数值化的前缀编码集合的长度. 与PPTQ相比,BPTQ的Cs减小了约91.19%.
2) 以感知节点数量n为自变量,其他参数保持初始设置不变,考查n对感知节点通信代价的影响,实验结果如图 2所示. 随着n的增长,PPTQ和BPTQ产生的Cs均有所增加,其中PPTQ 增幅较大,而BPTQ增幅较小. 与PPTQ相比,BPTQ所产生的Cs平均减小了约91.17%,原因与上述实验相同.
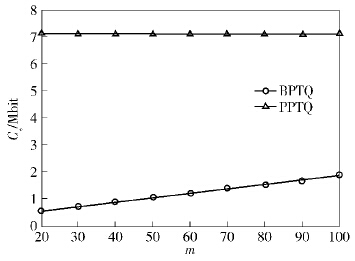
3) 以桶划分数量m为自变量,其他参数保持初始设置不变,考查m对感知节点通信代价的影响,实验结果如图 3所示. 显然,桶划分数量m不影响PPTQ所产生的Cs,因为PPTQ并未用到桶划分技术. 随着m的增长,BPTQ所产生的Cs也随之增加,其原因是桶划分数量增加之后,感知节点上传的桶内感知数据的数量索引信息量也增加,因此增加了通信代价. BPTQ所产生的Cs与PPTQ相比,平均减小了约82.17%,原因与前述实验相同.
4.2 查询处理通信代价对比实验这里实验参数的初始设置与4.1节相同,分别以k和m为自变量,对比BPTQ和PPTQ中查询处理过程的通信代价CQ.
1) 以k为自变量,其他参数设置保持初始值不变,得到图 4所示的实验结果. 随着k的增长,PPTQ所产生的CQ成线性增长,而BPTQ在初期的变化不明显,后期略有上升的趋势. 当k较小时,PPTQ所产生的CQ小于BPTQ;而随着k增大,BPTQ的表现显著优于PPTQ.
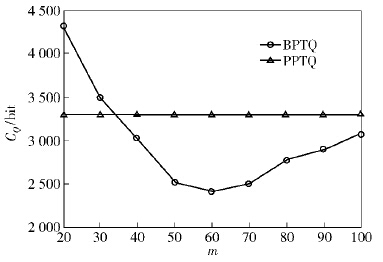
2) 以m为自变量,其他参数设置保持初始值不变,得到图 5所示的实验结果. 随着m的增长,PPTQ所产生的CQ保持不变,因为PPTQ未用到桶划分技术;BPTQ所产生的CQ呈现出先快速下降后缓慢上升的趋势,在本实验参数条件下,CQ在m=60时取得极小值. 随着桶划分数量的增长,BPTQ中SM上传的冗余密文数据相对减少,因此CQ呈下降趋势;但是随着m的进一步增长,SM上传给基站的桶索引信息也会相应增加,当桶索引信息的增长幅度超过冗余数据密文的减小幅度时,CQ便开始增长.
综上可知,与现有研究工作PPTQ相比,BPTQ产生的感知节点通信代价显著低于PPTQ;桶划分策略的选择对BPTQ的查询处理通信代价的影响较大,选择适当的桶划分策略,可以有效降低BPTQ的查询处理通信代价;随着查询参数k的增大,BPTQ的查询处理通信代价显著优于PPTQ.
5 结束语针对两层传感网络的安全数据查询问题,提出了一种用于两层传感器网络的BPTQ方法. 该方法通过引入桶划分策略和加密技术,能够确保感知数据在存储、通信及查询处理过程中隐私安全性. 理论分析和实验结果表明,BPTQ方法是一种高效的具有隐私保护能力的Top-k查询处理方法.
| [1] | Gnawali O, Jang K Y, Paek J, et al. The tenet architecture for tiered sensor networks[C]//4thACM Conference on Embedded Networked Sensor Systems, 2006 ACM. Colorado: ACM Press, 2006: 153-166.[引用本文:2] |
| [2] | 戴华,杨庚,秦小麟,等. 面向隐私保护的两层传感网Top-k查询处理方法[J]. 计算机研究与发展,2013,50 (6):1239-1252. Dai Hua, Yang Geng, Qin Xiaolin, et al. Privacy-preserving top-kquery processing in two-tiered wireless sensor networks[J]. Journal of Computer Research and Development, 2013 50(6): 1239-1252.[引用本文:2] |
| [3] | Zhang Rui, Shi J, Liu Y, et al. Verifiable fine-grained Top-k queries in tiered sensor networks[C]//29th IEEE International Conference on Computer Communications (INFOCOM2010). San Diego: IEEE, 2010: 1199-1207.[引用本文:1] |
| [4] | Dai Hua, YangGeng, HuangHaiping, et al. Efficient verifiable top-k queries in two-tiered wireless sensor networks[J].KSII Transactions on Internet and Information Systems,2015, 9(6):2111-2131.[引用本文:1] |
| [5] | Yu Chiamu ,Ni Guokai, Chen Ingyi, et al. Top-k query result completeness verification in tiered sensor networks [J]. IEEE Transactions on Information Forensics and Security, 2014, 9(1): 109-124.[引用本文:1] |
| [6] | Hacigumus H, Iyer B R, Li Chen, et al. Executing SQL over encrypted data in the database service provider model [C]//2002 ACM SIGMOD International Conference on Management of Data. Wisconsin: ACM Press, 2002: 216-227.[引用本文:2] |
| [7] | Das G, Gunopulos D, Koudas N, et al. Answering top-k queries using views[C]//32ndInternational Conference on Very Large Data Bases. Seoul, Korea: ACM Press, 2006: 451-462.[引用本文:1] |
| [8] | Bozovic V, Socek D, Steinwandt R, et al. Multi-authority attribute-based encryption with honest-but-curious central authority [J]. International Journal of Computer Mathematics, 2012, 89(3): 268-283.[引用本文:1] |