无线自组织网络^[1-2]中的节点通常由电池供电，价格昂贵，有时甚至无法重新充电设备^[3].因此，能耗问题是无线自组织网络的一个重要研究课题^[4].该问题的一种缓解方法就是在自组织网络时能构建一个双连通图，并且找出该图的最小能耗^[5].

笔者提出了一种基于扩展生成树的新算法，即具有路径重链接的贪婪随机自适应搜索程序(GRASP, greedy randomized adaptive search procedure)^[1]算法，在自组织网络中构建双连通图，提高了网络的容错能力.

构建阶段的第1部分：每次构建双连通图的1个节点，给定节点集V和非负弧权重e(u, v)，任意u, v∈V，针对所有u∈V，算法设置功率p_u=0，初始化工作图为

(1)

其中：E(p)={[u, v]:u∈V′, v∈V′, p_u≥e(u, v), p_v≥e(v, u)}=∅，V′={r}，r∈V为任意随机选择的初始节点.基于无线多播性质引导构建的贪婪函数：若p_u是分配给节点u的当前功率，且存在节点v，使e(u, v) > p_u，则建立从u到v的通信所需的增量功率为e(u, v)－p_u，因此贪婪成本函数为g(u, v)=max{0, e(u, v)－p_u}+max{0, e(u, v)－p_v}，其中任意u, v∈V.若g(u, v)=0，则已经建立u和v之间的双向通信.

对于每个节点u∉V′，令g(u)=为连接它到V′中1个节点的最小功率增量，令和分别为所有候选节点上的最小和最大功率增量(不在当前解中).受限候选列表(RCL, restricted candidate list)由所有节点u∈V\V′形成，以便，且0≤α≤1.显然α=0的情况对应于纯贪婪算法，而α=1等价于随机构建.节点u从RCL中随机选择，插入V′，分别通过最大化{0, e(u, v)－p_u}和最小化{0, e(u, v)－p_v}增加节点u∈V\V′和v∈V′的功率分配.因此，双向边(u, v)插入E(p)，当V′=V时，迭代停止，得到连通图H(p)=(V, E(p)).

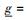
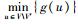
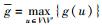
构建阶段的第2部分：构建双连通图G(p)=(V, B(p)).连接那些不是当前解的关节点的新边不直接由算法连接，逐步减少双连接组件数，直到获得双连通图.使用第1部分获得的值初始化功率分配，因此，边集初始化为B(p)=E(p)，参照文献[6]，将其用于计算双连接组件和解的关节点.

第2部分RCL由所有不是关节点的节点形成，使，且0≤α≤1.不是关节点的节点u随机从RCL中选择，对于一些不是关节点的节点v，有g′(u)=g(u, v)，分别通过max{0, e(u, v)－p_u}和max{0, e(u, v)－p_v}增加节点u和v的功率分配.双向边(u, v)插入B(p)，且新迭代重新开始，因此至少减少1个通过边连接的任意2个双连接组件数，当构建出双连通图时，算法停止.

定义P_i=[p_i¹, p_i², …, p_i^ϕ(i)]为由仅有效增加的可分配给每个节点i∈V的功率级别形成的列表；对于给定的功率分配p={p_i:i∈V}，令S_i=(s_i¹, s_i², …, s_i^ϕ(i))为具有组件s_i^l∈{0, 1, 2}的一个向量；定义节点集合T_i^l，将V中所有节点到i的距离从小到大排序，T_i^l表示与第i个节点距离排名为l的节点集合，以图 1为例，T_a¹={b}、T_a²={c, d}、T_a³={e}、T_a⁴={f}.

图 1

图 1

图 1 节点集合示例

针对l=1, 2, …, (i)，对于每个i∈V，有：

若p_i^l > p_i，s_i^l=0(以小于p_i^l的功率分配操作节点i)；若p_i^l≤p_i且存在1个节点j∈T_i^l和级别k=1, 2, …, ϕ(j)，使p_j≥p_j^k，i∈T_j^k(表示功率级别p_i^l支持节点j的双向边)，s_i^l=2，否则s_i^l=1(使用功率级别p_i^l，但仅建立从i到j的非双向弧).

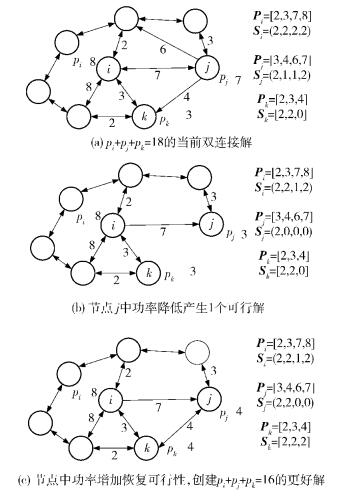
利用2个基本操作改变功率进行局部搜索.作用于节点j∈V(见图 2(b))，第1个操作降低其当前功率分配p_j=p_j^l(l≥2) 到p_j=p_j^l′，其中l′为支持双向边的最高级别：1≤l′≤l，s_j^l′=2，s_j^l″=1，对于所有l″=l′+1, …, l－1.它移除节点i和j之间链路(弧和边)，对所有j∈T_j^l′+1∪…∪T_j^l－1∪T_j^l，总功率分配降低到p_j^l－p_j^l′.

图 2

图 2

图 2 局部搜索移动

作用于节点j∈V(见图 2(c))，第2个操作增加其当前功率p_j=p_j^l(l≤ϕ(j)－1) 到p_j=p_j^l+1，若存在1个节点i∈T_j^l+1和1个功率级别k=1, 2, …, (i)，使p_i≥p_i^k和i∈T_j^l，则目标函数增加到p_j^l+1－p_j^l；否则，令i∈T_j^l+1，使p_i－p_i^k(i)=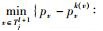j∈T_v^k(v), k(v)=1, 2, …, (v)}.这种情况中，该操作增加当前功率p_i到p_i^k(i)，目标函数增加到(p_j^l+1－p_j^l)+(p_i^k(j)－p_i)，功率增加操作确保双向边(i, j)的插入.

局部搜索阶段，通过减少打破双连接性所需节点的功率分配以搜索当前解的邻域，如图 2所示.

减少那些增加功率的操作可加速局部搜索，因此，构建一个候选列表，节点利用目标函数中对应的增量排序，当功率降低操作破坏掉双连接性时，计算双连接组件，实现2种加速度方案：① 减少方案，功率增加操作受限于节点对，该节点对属于受前一个减小操作影响的节点对的同一双连接组件；② 扩展方案，考虑功率增加操作，涉及来自不同双连接组件的任意节点对.

依赖所用的加速方案，实现3种局部搜索程序：① 减少局部搜索，使用减少方案；② 扩展局部搜索，使用扩展方案；③ 混合局部搜索，使用减少方案，直到找不到进一步改进的移动，再使用扩展方案.

算法1给出了具有路径重链接的GRASP启发式算法的伪代码，对双连接最小能耗问题的非对称输入图和双向解使用混合局部搜索程序.第1) 行初始化目标值；第2) 行将精英解的池Elite_Set初始化为空；第3)~19) 行中循环的每次迭代寻找对问题的新解，直到达到最大迭代数；第4) 行寻找1个贪婪随机解，并将其提交给第5)~10) 行中的局部搜索程序，混合局部搜索运用减少方案，直到不再有任何改进，然后运用扩展方案，若扩展方案找到更好的解，则通过减少局部搜索再次探索其邻域，直到不再有任何改进，路径重链接应用于第12) 行，更新第14) 行中的精英集，若路径重链接找到改进前发现的最优解，则分别更新第16) 和17) 行中的最优解和相应的值；第20) 行返回最优功率分配p^*.

算法  具有路径重链接的GRASP启发式算法

要求：节点集V、权重e(u, v):∀u, v∈V、Max_Iterations和Seed

确保：最知名解p^*

1) f^*←∞；   //初始化目标值

2) Elite_Set←∅；

3) for迭代=1, 2, …, Max_Iterations do

      //迭代寻找问题的新解

4) p←Greedy_Randomized_Construction(Seed)

5) Repeat  //局部搜索

6)  p←Reduced_Local_Search(p)；

7)  if无改进then

8)   p←Extended_Local_Search(p)；

9)    end if

10)   until无改进

11)    if Elite_Set≠∅ then

12)    p←patch_Relinking(p, Elite_Set)；

    //路径重链接

13)    end if

14)    Update_EliteSet(p, Elite_Set)；

15)    if f(p) < f^* then

16)   p*←p；//更新最佳解

17)   f^*←f(p)；

18)  end if

19) end for

20) return p^*；//返回最佳功率

为了验证所提算法的有效性，本节在2类具有10~800个节点的随机生成的非对称测试问题上执行计算实验.所有实验均在英特尔酷睿2四核处理器上运行，系统为GNU/Linux 2.6.24，机器配置2.40GHz时钟和8GB RAM，利用CPLEX 11.0作为整数规划求解器.节点在单位正方形网格中均匀分布，节点之间弧的权重由以下2种方式得到. 1) 欧氏实例：节点u, v∈V之间弧的权重为e(u, v)=Fd_{u, v}^ε，其中d_{u, v}为节点u和v之间的欧氏距离，损耗指数ε设置为2，F∈[0.8, 1.2]为均匀分布生成的随机扰动. 2) 随机实例：节点u, v∈V之间的弧权重e(u, v)在(0, 1]中随机生成.

考虑使用各种局部搜索程序和路径重链接策略的4种GRASP变种：① GRASP-R，使用减少局部搜索；② GRASP-X，使用扩展局部搜索；③ GRASP-M，使用混合局部搜索；④ GRASP-Mpr，使用具有路径重链接的混合局部搜索.其中，减少局部搜索、扩展局部搜索、混合局部搜索如1.2节所述.

使用文献[7]描述的具有概率分布的每100次迭代后更新的反应策略设置参数α，路径重链接处理的精英集大小限制为5.表 1描述了有100个节点的实例运行5次的平均目标值.由表 1可以看出，运行时间限制从25s增加到625s，所有启发式算法的变种随时间限制增加而改进它们的解. GRASP-Mpr算法在大部分情况下都能找到最优平均解值.

表 1

表 1

表 1 具有100个节点的实例的平均总能耗和时间

表 1 具有100个节点的实例的平均总能耗和时间

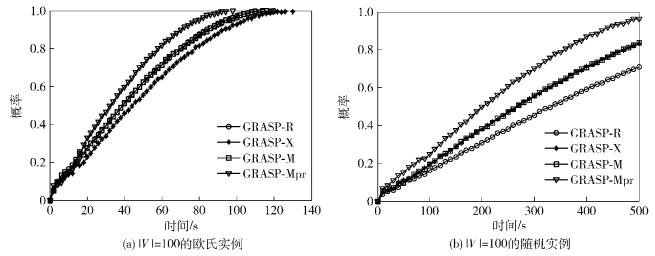
图 3描述了|V|=100的2个实例的结果，使用它们的优化值作为目标.从图 3中可以看出，当追寻更困难目标解时，GRASP-Mpr算法是在|V|=100的环境中运行最快的算法.图 3中的不完整绘制表明，除了最快的GRASP-Mpr算法之外的所有算法多次运行在15min内无法到达目标值.变种算法中2个加速度的组合为局部搜索带来了更多多样化，而路径重链接用作集约化策略，多样化和集约化提高了在较短时间内寻找良好解的概率.

图 3

图 3

图 3 GRASP对目标解值的经验时间分布(100个节点)

表 2、表 3比较了MST-aug算法、贪婪算法和GRASP-Mpr算法在大型问题上的能耗和节点度.

表 2

表 2

表 2 MST-aug、贪婪算法和GRASP-Mpr算法的总能耗

表 2 MST-aug、贪婪算法和GRASP-Mpr算法的总能耗

表 3

表 3

表 3 MST-aug、贪婪算法和GRASP-Mpr算法的平均节点度

表 3 MST-aug、贪婪算法和GRASP-Mpr算法的平均节点度

由表 2可看出，GRASP-Mpr算法的能耗比MST-aug算法和贪婪算法都少.具体而言，欧氏实例中，相比MST-aug算法，所提算法总能耗平均改善了37.85%，相比贪婪算法平均改善了5.39%；随机实例中，相比MST-aug算法，所提算法总能耗平均改善了74.63%，相比贪婪算法平均改善了3.15%.因为GRASP-Mpr的计算时间固定(实验中设为10min)，执行的迭代次数随着实例大小增加而减少.根据表 1可知，若固定计算时间，GRASP-Mpr甚至对更大的实例也能获得更好的解.

由表 3可看出，GRASP-Mpr算法产生的解的平均节点度范围为2.50~2.67，比MST-aug找到的解小得多，这是因为双连通图中任意节点度至少为2，表明GRASP-Mpr解值非常接近最佳可能下界，即精确优化解.而且，平均节点度范围还表明贪婪算法和GRASP-Mpr算法获得的良好解独立于实例大小.

表 4、表 5给出了MST-aug算法、贪婪算法和GRASP-Mpr算法的边干扰和节点干扰.从表 4、表 5可看出，相比其他几种算法，GRASP-Mpr算法的边干扰值和节点干扰值均为最小，体现了GRASP-Mpr算法较强的抗干扰能力.

表 4

表 4

表 4 MST-aug、贪婪算法和GRASP-Mpr算法的边干扰

表 4 MST-aug、贪婪算法和GRASP-Mpr算法的边干扰

表 5

表 5

表 5 MST-aug、贪婪算法和GRASP-Mpr算法的节点干扰

表 5 MST-aug、贪婪算法和GRASP-Mpr算法的节点干扰

考虑无线自组织网络中节点的分配传输功率和容错能力问题，提出了一种具有路径重链接的GRASP启发式算法.该算法产生双连通网络，提高了容错能力，再进行局部搜索优化功率分配，减少能耗，延长了网络寿命.仿真结果表明，GRASP-Mpr能极快地找到良好解，对于具有高达800个节点的较大型问题，GRASP-Mpr优于其他几种著名的启发式算法.