为了准确全面地评估计算机网络的脆弱性, 对攻击图中存在的攻击环路、状态爆炸、难以量化分析等问题进行了研究, 提出了属性攻击图向贝叶斯网络转化的方法和新的环路消除算法, 并利用这2个算法建立贝叶斯属性攻击图模型.在该模型中, 利用贝叶斯公式进行推导, 得到评估指标的计算公式.利用通用漏洞评分系统数据计算节点的发生概率和评估指标, 进行计算机网络脆弱性评估.通过实验分析, 证明了该模型的可行性和有效性.与其他的脆弱性评估方法相比, 该模型具有评估准确、计算简洁、动态量化评估的特点.
For assessing the vulnerability of computer network accurately and comprehensively, the problem of attack loops, the state explosion and analyzing qualitatively were researched. The method of converting attribute attack graph to the Bayesian network and the new loop elimination algorithm was also proposed. By using these two algorithms, a new Bayesian attribute attack graph model was build. The formula of assessing indicators was derived by Bayesian formula. The data of common vulnerability scoring system was used to compute the probability of attribute nodes and indicators to conduct network vulnerability assessment. Experiments analysis proves the feasibility and effectiveness of the model. Compared with other methods of vulnerability assessment, this model has simple calculation which is suitable for dynamic quantitative assessment.
近年来,众多学者运用攻击图技术分析网络的脆弱性[1]. Sheyner等[2]给出了状态攻击图自动生成方法,陈锋等[4]、Wang等[7]利用属性攻击图避免了状态爆炸现象,叶云等[10]研究了攻击图中含圈路径的问题,陈思思等[5]、贾炜[8]利用状态攻击图评估网络脆弱性,方研等[6]、Poolsappasit等[9]在属性攻击图中计算原子攻击发生的概率.
笔者提出了一种新的属性攻击图贝叶斯网络评估模型.该模型具有以下优点:① 新的含圈路径处理方法,避免大量信息丢失;② 给出了属性攻击图向贝叶斯网络的转换方法(该方法可以方便贝叶斯网络的推理计算,给出了将属性攻击图中4种结构的节点向贝叶斯网络转化的方法,同时给出了新的节点发生的概率计算方法).利用该模型进行网络脆弱性评估可以达到减少信息丢失、得到不含有混合节点的模型、简化概率计算的目的,评估结果更加准确、可靠.
1 模型建立属性攻击图是一种有向无环图,它含有2种节点:属性节点和原子攻击节点.贝叶斯网络是一个有向无环图,具有因果关系和概率语义,可以根据已知的信息对未知的结果或原因进行推理和预测.在贝叶斯网络中,节点的状态及发生概率只与其父节点有关,在攻击图中网络脆弱点是否被利用也只与攻击路径中的父节点有关,这种节点关系在贝叶斯网络和攻击图中相对应;贝叶斯网络和攻击图都是一种有向无环图,并且有向边表示一种因果关系.因此可以将贝叶斯网络和攻击图进行结合,对网络的脆弱性进行量化评估.
1.1 模型定义定义 贝叶斯网络属性攻击图表示为B_GRA < A, E, P >.其中,A表示属性节点集合;E表示有向边集合,即原子攻击;P表示属性节点被利用的条件概率表.任意节点用a表示,其父节点集合为Ain(a),其子节点集合为Aout(a).
B_GRA满足以下条件:
∀E⊆A×A对∀e∈E,都有e=Ein(e)→Eout(e),其中Ein(e)表示原子攻击的条件属性,Eout(e)表示原子攻击的结果属性,“→”表示2个属性节点之间的因果关系.
条件独立性假设:在给定父节点的条件下,其子节点a独立于它的非子节点,设节点a的父节点为Ain(a),非子孙节点为Πout(a),用概率公式表示为
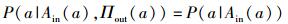
|
(1) |
属性节点A是一个二元变量,只有2种状态,A为false时表示攻击者已经获得该属性,A为true时表示攻击者还未获得该属性.
构建贝叶斯网络属性攻击图模型主要涉及2方面:模型网络结构的构建和节点发生概率的计算.下面主要从模型的结构(1.2节)和节点的计算(1.3节)介绍如何构建贝叶斯网络属性攻击图模型.
1.2 结构转换在攻击图中,属性节点用矩形表示,原子攻击节点用椭圆形表示.当原子攻击的条件属性全部满足时,原子攻击才会发生;当原子攻击成功后会产生攻击影响,提高攻击者的攻击能力,用结果属性表示攻击者获得的攻击能力,原子攻击节点代表了前后节点的因果关系.因此,将攻击图中的原子攻击抽象成贝叶斯网络中的有向边.下面将针对攻击图中父节点的关系,讨论4种节点结构的转化方法.
1) 顺序结构
原子攻击节点变换过程中最简单一种就是顺序结构变换,在攻击图中原子攻击的条件属性和结果属性各只有1个.在这种情况下,只需把原子攻击节点删除,用条件属性a1到结果属性a2的有向边表示原子攻击,即可转化为贝叶斯网络中的对应结构,如图 1所示.

|
图 1 顺序结构转化为贝叶斯网络 |
2) and结构
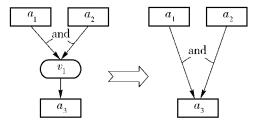
由属性攻击图的定义可知,原子攻击节点的父节点之间是“与(and)”的关系,只有当属性节点全部发生时原子攻击才会发生.对于有多个条件属性和1个结果属性的原子攻击节点,转化方法如下:将原子攻击节点删除,将每个条件属性到结果属性之间有1条有向边连接,用该有向边表示原子攻击,即条件属性和结果属性之间的因果关系.转化之后在贝叶斯网络结构中,条件属性之间的关系依然为“与(and)”关系,如图 2所示.
|
图 2 and结构转化为贝叶斯网络 |
3) or结构
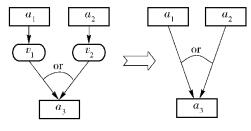
在攻击图中,属性节点的父节点之间是“或(or)”的关系,即父节点中的多个原子攻击只要有一个成功,攻击者就可获得结果属性.对于多个原子攻击有相同结果属性的情况,当原子攻击都只有一个条件属性时,转化方法如下:将原子攻击节点删除,条件属性到结果属性之间用有向边连接.在转化之后的贝叶斯网络中,条件属性之间仍为“或(or)”的关系,如图 3所示.
|
图 3 or结构转化为贝叶斯网络 |
4) 混合结构
在攻击图向贝叶斯网络转化的结构中,最复杂的就是混合结构的转化.混合结构是同时具有and结构和or结构,即多个原子攻击节点有相同的结果属性,且至少有1个原子攻击节点有多个条件属性.在这种结构中,如果将原子攻击节点全部删除,在结果属性节点的入边中既有and关系又有or关系,造成结构混乱,且不便于条件概率的计算.因此提出以下转换方法:将具有and关系的原子攻击节点去掉,结果属性节点上就会有混合关系,因此需要引入一个隐含混合属性节点temp.将and关系的入边指向temp节点,并且temp的出边指向结果属性,将只有1个条件属性的原子攻击节点删除,在条件属性到结果属性之间用1条有向边连接,如图 4所示.在该转化过程中,由于temp属性是a1、a2的混合属性,因此a1、a2到temp的有向边是必然成立的,即条件概率P(temp|a1, a2)=1,在1.4节中,式(5) 可以证明得到P(temp)=P(a1, a2).因此,在该转化之后,贝叶斯网络中节点的条件概率值以及节点之间的关系不会因为引入隐含属性节点而改变.

|
图 4 混合结构转化为贝叶斯网络 |
通过对攻击图中4种节点结构的转化,最终在得到的贝叶斯网络中只含有属性节点,有向边之间的关系只有and关系和or关系,同时将原子攻击体现在贝叶斯网络的有向边上.
1.3 消除含圈路径的算法在攻击图中经常会出现攻击环路.由于攻击者是智能的,即攻击者不会重复获得已经具有的攻击能力,且随着攻击的进行攻击者的能力是单调递增的,因此在攻击图中出现攻击环是不合理的,也不便于理解攻击过程.
叶云等[10]针对攻击图中的环路提出了各自的解决方案,主要是采取将环路的某些节点删除掉的方法.但是这些方法存在以下不足:① 删除节点的随机性较大;② 会造成丢失某些重要路径.针对这些不足,并且由于在实际网络环境中攻击难度最大的原子攻击发生的概率最低,提出了最难原子攻击消环算法,即消除环路中攻击难度最大的原子攻击,从而消除环路.
在介绍最难原子攻击消环算法之前,先给出原子攻击难度的度量指标和计算方法,该指标作为消环时选取目标原子攻击节点的标准.原子攻击是利用网络中的1个脆弱点进行的一次攻击,可以将脆弱点被利用的难易度进行量化作为原子攻击难度的度量值,该值可以用通用漏洞评分系统(CVSS, common vulnerability scoring system)评分计算得到. CVSS中基本评分(BM, base metrics)部分描述的是脆弱点的基本属性,其中包含6个指标,前3个指标是AV(access vector)、AC(access complexity)、AU(authentication),用于描述脆弱点的可用性. 3个CVSS指标的度量值根据可利用性分为3个等级:Low、Mid、High.分值越高,该脆弱点越容易被利用.由低到高,AV值依次为0.359、0.646、1.0;AC值依次为0.35、0.61、0.71;AU值依次为0.45、0.56、0.704.
在CVSS中,脆弱点的可用性指标定义为E=20VCU(0≤E≤10). Ex的值越小,表示原子攻击的难度越大.由于可用性与攻击难度成反比关系,因此根据这3个指标计算原子攻击的难度,用D表示相应原子攻击的难度,其值越大攻击难度越大,计算公式为

|
(2) |
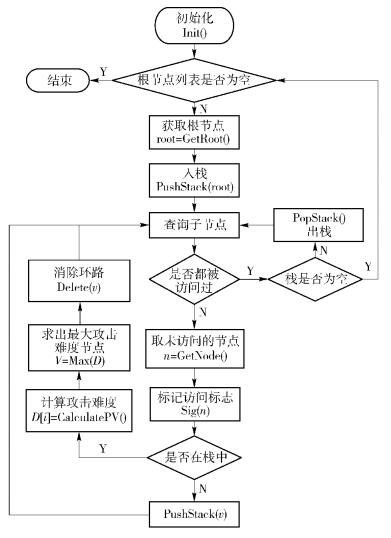
最难原子攻击消环算法思想:该算法的输入是一个可能含环路的攻击图,将攻击图的入口节点加入到根节点数组中,初始化一个栈用来存放找到的环路.从一个入口根节点进行深度优先遍历,不断地访问子节点,将访问到的子节点进行标记并压入栈,直到不存在子节点或访问的节点在栈中已经出现为止.当子节点在栈中已经存在时,栈中存储了一个环路,此时计算环路中的原子攻击难度,找出难度最大的原子攻击节点,删除它的出边,消除环路.在遍历时,如果子节点不存在,则进行回溯,将栈中节点出栈,查询新的未被访问的子节点重复上述深度优先遍历过程.当栈为空时,则以该入口根节点为起始节点的遍历完成,从下一个新的入口根节点开始按上述方法遍历.直到所有的入口根节点都遍历完,则整个攻击图消环完成,此时得到一个无环的攻击图.消除环路的算法流程如图 5所示.
|
图 5 消环算法流程 |
1) and型节点
计算图 2的贝叶斯网络中a3节点属性的概率,由于a3节点的父节点是and关系,所以只有当父节点全部发生时,攻击者才能获得子节点的属性.此时攻击者获得a3属性的概率为
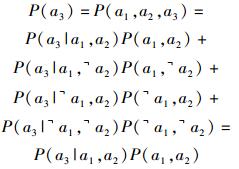
|
(3) |
2) or型节点
计算图 3的贝叶斯网络中a3节点属性的概率,由于a3节点的父节点是or关系,所以当父节点只要有1个发生时,攻击者就可以获得子节点的属性.此时攻击者获得a3属性的概率为
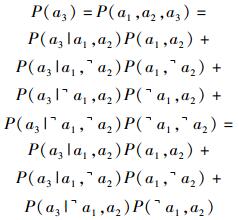
|
(4) |
3) 临时节点
计算图 4中temp节点属性的概率,由1.2节中节点转化过程可知,在图 4中转化后的贝叶斯网络中临时节点的条件概率为1,即P(temp|a1, a2)=1.由于临时节点的父节点都是“and”关系,此时攻击者获得temp节点属性的概率为

|
(5) |
4) 攻击路径成功的概率
设攻击者要获得的目标属性为obj,在攻击路径上obj的所有直接和间接父节点为Pre(obj),直接父节点为DPre(obj),则目标节点受到攻击的概率为

|
(6) |
由于贝叶斯网络中条件独立性的假设,式(6) 可以改写为

|
(7) |
迭代式(7),就可求得目标属性在该攻击路径中被攻击的概率.在图 4中,目标a4被攻击的概率为P(a4)=P(a4|temp)P(temp|a1, a2)P(a1)P(a2).假设a1、a2的先验概率分别为0.2、0.3,攻击者达到a4的概率为P(a4)=0.018.若网络管理员或IDS发现攻击者已经获得a1属性,则P(a1)=1,再次计算得P(a4)=0.09,因此加入攻击证据a1后,a4受到攻击的概率明显增大,这与预期的结果一致.
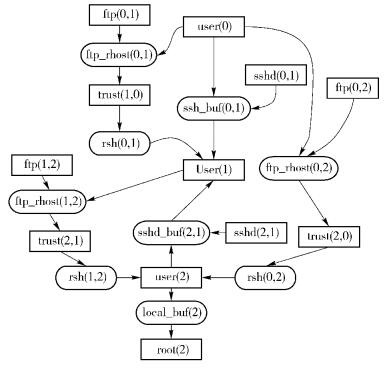
2 实验分析为了验证检测模型的可行性、有效性,较多学者采用方研等[6]的实验环境构建攻击图,笔者也依照其方法搭建了实验环境,并且构建了如图 6所示的属性攻击图.本节利用属性攻击图(见图 6) 建立贝叶斯网络属性攻击图(见图 7).图 6中矩形代表属性节点,椭圆形代表原子攻击节点,共有3个主机编号:0、1、2,其中0号主机连接外网,1号、2号主机在局域网内部,攻击的目标是2号主机,获得其root权限.
|
图 6 属性攻击图 |

|
图 7 贝叶斯网络属性攻击图 |
从图 6中可以看出,存在环路:user(1)→ftp_rhost(1, 2)→trust(2, 1)→rsh(1, 2)→user(2)→sshd_buf(2, 1)→user(1).
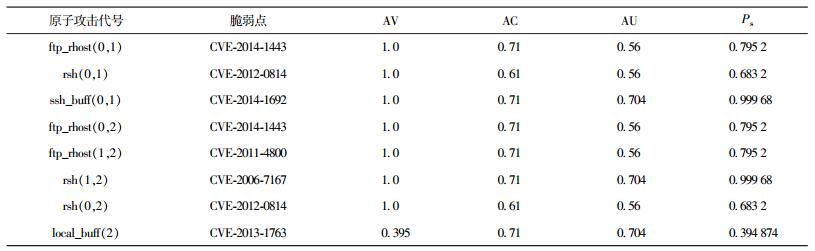
根据脆弱点的公共漏洞和暴露(CVE, common vulnerabilities and exposures)编号查阅漏洞数据库中CVSS相关属性的评分,得到环路中3个原子攻击脆弱点相关信息,如表 1所示.
|
|
表 1 脆弱点各属性值 |
利用1.3节中攻击难度的计算式(2),计算环路中3个原子攻击节点的D值:D{ftp_rhost(1, 2)}=2.52,D{rsh(1, 2)}=2.00,D{sshd_buf(2, 1)}=5.57.
从结果中得出,sshd_buf(2, 1) 脆弱点的攻击难度最大,根据1.3节中攻击图消环算法,断开该脆弱点的出边,消除环路得到无环属性攻击图.在该无环攻击图中,保留的原子攻击是最可能发生的,符合攻击的实际情况,即容易成功的原子攻击最可能被攻击者利用.根据1.2节中的转化方法,将无环属性攻击图转换为贝叶斯网络,得到贝叶斯网络属性攻击图.在该过程中,攻击图只损失了最不可能发生的原子攻击,其损失的节点信息很少,如图 7所示.
2.2 概率计算利用图 7的贝叶斯网络属性攻击图,根据1.4节中推导的式(6) 或式(7),可以计算攻击路径成功的概率,利用这个指标评价网络的脆弱性.从图 7中可以得到3条攻击路径:
1) Path_1:[ftp(0, 1) and user(0)]→[trust(1, 0)]→[user(1) and ftp(1, 2)]→[trust(2, 1)]→[user(2)]→[root(2)];
2) Path_2:[user(0) and sshd(0, 1)]→[temp]→[user(1) and ftp(1, 2)]→[trust(2, 1)]→[user(2)]→[root(2)];
3) Path_3:[user(0), ftp(0, 2)]→[trust(2, 0)]→[user(2)]→[root(2)].
在贝叶斯网络中属性节点之间的有向边代表原子攻击被利用的过程,原子攻击难度越大脆弱点被利用的概率就越低,两者成反比关系.因此,可以用原子攻击的难度代表属性节点之间的条件概率,定义条件概率为
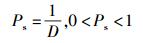
|
(8) |
脆弱点被成功利用的条件概率如表 2所示.
|
|
表 2 脆弱点被成功利用的条件概率表 |
由文献[4]给出ftp(0, 1)、user(0)、ftp(0, 2)、ftp(1, 2)、sshd(0, 1)5个节点的先验概率为0.6、0.3、0.4、0.7、0.5.利用表 2中的数据和1.4节中的式(7) 可以计算得到不同条件下攻击路径成功的概率,如表 3所示.
|
|
表 3 攻击路径成功概率 |
通过对比表 3中的数据可以发现,在给出P(ftp_rhost(0, 1))=1、P(sshd(0, 1))=1、P(ftp_rhost(0, 2))=1的证据后,与证据相对应的攻击路径Path_1、Path_2、Path_3成功的概率分别增大.同样,由于user(0) 在3条攻击路径中都出现,因此在给出P(user(0))=1的证据后,Path_1、Path_2、Path_3成功的概率均增大.在实际情况中,攻击者获得的属性越多,即证据越多,攻击成功的可能性越大.从上述分析可以看出,在增加证据的时候,攻击成功的可能性增大,实验数据与实际的情况相符合.因此,建立的贝叶斯网络属性攻击图可以从概率的角度进行量化评估计算机网络受到攻击的可能性大小,利用该模型可以有效地对计算机网络的脆弱性进行评估.
2.3 对比分析叶云等[10]在相同的攻击图模型中,利用其消环算法得到环路中第1条遍历到的路径为通路,删除环路中的其他节点,消除含圈路径.当用这种方法处理攻击图中含圈路径时,在图 6中,删除不同原子攻击会造成攻击路径的丢失,在表 4中可以看出,如果删除另外2个原子攻击将会导致2条路径的丢失.采用所提出的方法处理含圈路径,只会丢失sshd_buf(2, 1)1个节点,最终得到Path_1、Path_2、Path_3 3条攻击路径.从表 3中可以看出,在没有证据的情况下,若用前一种消环方法,网络中最脆弱的地方在Path_3处,被攻击的概率为0.0258;若用所提出的消环方法,网络中最脆弱的地方在Path_2处,被攻击的概率为0.03276.对比发现,利用所提出的方法发现的攻击路径所发生的概率比较大,可以发现更加危险的攻击路径,为网络管理员提供更加有效的加固方案,因此所提出的方法更准确.
|
|
表 4 删除不同原子攻击丢失的路径 |
在文献[6]中建立的贝叶斯网络模型B-AC包含3类节点:or、and、mix,其中mix节点是由其余2种节点组合得到的.在计算节点概率时mix节点需要考虑or和and 2种情况,使得概率的计算变得复杂.笔者通过引入临时节点temp,将mix节点的2种关系分离,计算节点发生的概率时仅由1种基本公式即可,简化了概率计算.
早期的基于规则的评估方法[8]是基于历史攻击事件的,因此当攻击路径Path_1、Path_2发生过,而攻击路径Path_3没有发生过,则规则库中将只有Path_1、Path_2的规则,只能定性地预测出Path_1、Path_2攻击路径有可能被利用.
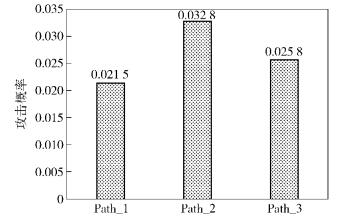
相对于早期的基于规则的评估方法而言,利用所提出的评估方法,对同一目标得出多条可能的攻击路径,并计算出每条攻击路径被利用的概率.从图 8中可以得知,利用所提模型可以预测出Path_1、Path_2、Path_3 3条攻击路径以及被利用的概率,并且对比后可知Path_2被利用的概率最大.
|
图 8 不同攻击路径预测概率对比 |
笔者提出了属性攻击图向贝叶斯网络转化的方法和属性攻击图中消除环路的算法.在模型中,给出攻击路径被成功利用的概率计算公式,用于评估网络的脆弱性.通过实验分析,利用提出的转换方法可以得到贝叶斯网络属性攻击图,简化了节点发生概率的计算;利用提出的环路消除算法,可以减少重要攻击路径信息的丢失,提高评估的准确度.同时,所提出的评估方法也有不足,对于贝叶斯网络的推理算法还有待改进.
| [1] |
钟尚勤, 徐国胜, 姚文斌, 等. 基于主机安全组划分的网络安全性分析[J]. 北京邮电大学学报, 2012, 35(1): 19–23.
Zhong Shangqin, Xu Guosheng, Yao Wenbin, et al. Network security analysis based on host-security-group[J].Journal of Beijing University of Posts and Telecommunications, 2012, 35(1): 19–23. |
| [2] | Sheyner O, Haines J, Jha S, et al. Automated generation and analysis of attack graphs[C]//Proceedings 2002 IEEE Symposium on Security and Privacy, 2002: 273-284. |
| [3] |
龙门, 夏靖波, 张子阳, 等. 节点相关的隐马尔可夫模型的网络安全评估[J]. 北京邮电大学学报, 2011, 33(6): 121–124.
Long Men, Xia Jingbo, Zhang Ziyang, et al. Network security assessment based on node correlated HMM[J].Journal of Beijing University of Posts and Telecommunications, 2011, 33(6): 121–124. |
| [4] |
陈锋, 张怡. 基于攻击图的网络脆弱性量化评估研究[J]. 计算机工程与科学, 2010, 32(10): 8–11.
Chen Feng, Zhang Yi. Research of quantitative vulnerability assessment based on attack graphs[J].Computer Engineering and Science, 2010, 32(10): 8–11. doi: 10.3969/j.issn.1007-130X.2010.10.003 |
| [5] |
陈思思, 连一峰, 贾炜. 基于贝叶斯网络的脆弱性状态评估方法[J]. 中国科学院研究生院学报, 2008, 25(5): 639–648.
Chen Sisi, Lian Yifeng, Jia Wei. A network vulnerability evaluation method based on Bayesian networks[J].Journal of the Graduate School of the Chinese Academy of Sciences, 2008, 25(5): 639–648. |
| [6] |
方研, 殷肖川, 李景志. 基于贝叶斯攻击图的网络安全量化评估研究[J]. 计算机应用研究, 2013, 30(9): 2763–2766.
Fang Yan, Yin Xiaochuan, Li Jingzhi. Research of quantitative network security assessment based on Bayesian-attack graphs[J].Application Research of Computers, 2013, 30(9): 2763–2766. |
| [7] | Wang Lingyu, Yao Chao, Singhal A, et al. Interactive analysis of attack graphs using relational queries[M]. Data and Applications Security XX: Springer Berlin Heidelberg, 2006: 119-132. |
| [8] |
贾炜. 计算机网络脆弱性评估方法研究[D]. 合肥: 中国科学技术大学, 2012.
Jia Wei. The research on computer network vulnerabilities assessment methods[D]. Hefei: University of Science and Technology of China, 2012. |
| [9] | Poolsappasit N, Dewri R, Ray I. Dynamic security risk management using Bayesian attack graphs[J].Dependable and Secure Computing, IEEE Transactions on, 2012, 9(1): 61–74. doi: 10.1109/TDSC.2011.34 |
| [10] |
叶云, 徐锡山. 基于攻击图的网络安全概率计算方法[J]. 计算机学报, 2010(10): 1987–1996.
Ye Yun, Xu Xishan. An attack graph based probabilistic computing approach of network security[J].Chinese Journal of Computers, 2010(10): 1987–1996. |