2. 清华大学 自动化系, 北京 100084;
3. 东南大学 移动通信国家重点实验室, 南京 210009
认知无线电网络中, 受当前频谱感知和功率分配概念的束缚, 次用户系统的频谱利用率和信道容量仍十分有限.分析了传统的认知无线电框架, 提出了一种基于连续感知信息的普适性框架, 即次用户在得到感知信息后, 不再对主用户是否存在进行二元判决, 而是根据连续感知信息直接进行功率分配.分别在连续功率分配和多电平功率分配的场景下进行了数学建模, 分析结果表明, 所提出的普适性框架给出了认知无线电系统性能的理论上限, 而传统的3种认知无线电框架仅是所提出的普适性框架的特殊情况.
2. Department of Automation, Tsinghua University, Beijing 100084, China;
3. State Key Laboratory of Mobile Communications, Southeast University, Nanjing 210009, China
In cognitive radio, restricted by the conventional concept of spectrum sensing and power allocation, the spectrum utilization and channel rate are both small. Conventional cognitive radio framework was analyzed. A continuous sensing information based generalized framework was proposed, where after obtaining the sensing information, the secondary user won't make decision on the presence of the primary user but directly decide the power allocation parameters under the power constraints. Cases of continuous and multiple-level power allocation rules were modeled and treated separately. It is shown that the proposed framework provides the upper bound of the theoretical capacity and the conventional architectures are its special cases.
目前,认知无线电的系统框架可概括为3种:① 衬底式,次用户在不进行频谱感知的情况下,把对主用户造成的干扰控制在一定门限之下实现频谱接入[1];② 机会式频谱接入,次用户通过频谱感知及决策,检测到没有被主用户占用的信道并接入[2];③ 基于频谱感知的频谱共享,次用户通过频谱感知及决策获取主用户信道占用情况,当信道被占用时,为减少对主用户的干扰,次用户采用小的发射功率,否则采用大的发射功率[3].
衬底式框架中,次用户使用固定的发射功率,而其他2种框架在频谱决策的基础上使用2个不同的发射功率,并分别对应于主用户空闲和存在的情况.综合来说,它们利用了固定或者单比特的发射功率,但这种方法不是最优的,通过将发射功率连续化,可以得到最优的功率分配算法.基于此,笔者提出一种基于连续感知信息的认知无线电普适性框架,即定义一个关于连续感知信息的功率分配函数,次用户在得到感知信息后不再对主用户是否存在进行决策,而是直接进行功率分配.最优的情况是功率分配关于感知信息为连续函数[4],但在实际的系统中,由于功率放大器等限制,发射功率只能取某些离散的值,因此也需要考虑离散功率分配函数的情况[5].
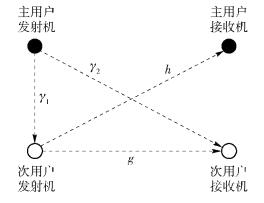
1 传统认知无线电框架分析考虑如图 1所示的认知无线电系统,主用户占用一个信道,g、γ1、γ2和h表示该信道上用户间的瞬时信道增益.假设1帧长度为T,其中频谱感知时间为τ,数据传输时间为T-τ.
|
图 1 典型的认知无线电系统组成 |
在时间τ内,次用户获取的感知信息可建模为
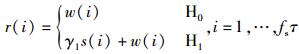
|
(1) |
其中:H0和H1分别表示主用户空闲与占用的假设;i为采样序列;s(i)为主用户发射信号,服从具有零均值和方差为Ps的复高斯分布;w(i)为零均值和方差为N0的加性高斯白噪声;fs为采样速率.
对感知信息r(i)计算累积能量作为最终的检验统计量,即
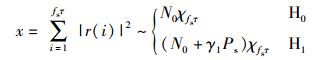
|
(2) |
其中χfsτ表示自由度为fsτ的中心卡方分布.
采用能量检测法进行频谱决策,假设检测门限为η,当x大于门限η时,判H1,否则判H0,则虚警概率和检测概率分别为
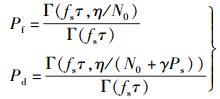
|
(3) |
其中:
基于频谱感知的频谱共享框架,当检测到主用户为空闲时,次用户使用大的发射功率P0,否则使用小的发射功率P1.则次用户的平均信道容量为

|
(4) |
其中P(H0)、P(H1)分别为主用户空闲和存在的概率.
对主用户产生的平均干扰约束可建模为
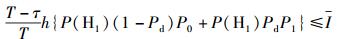
|
(5) |
在基于频谱感知的频谱共享框架下,数学模型为在式(5) 以及非负发射功率的约束下,最大化式(4),相关的求解可参考文献[4-5].
机会式频谱接入框架与基于频谱感知的频谱共享框架不同的是,当检测到主用户存在时,次用户保持静默,不进行传输(P1=0).该方式设置一个检测概率的门限Pdth,以保证对主用户造成的干扰小于一个等级.可以通过代入P1=0以及增加Pd≥Pdth,建立与式(4) 和式(5) 类似的数学模型.
衬底式框架的次用户不采用频谱感知,而是在对主用户造成某一门限干扰的约束下,实现自身的通信.可以通过代入P0=P1以及τ=0,建立与式(4) 和式(5) 类似的数学模型.
2 基于连续感知信息普适性框架分析2.1 认知无线电普适性框架的定性分析在传统的认知无线电框架中,由于学者们将频谱感知问题建模成式(1) 的标准二元检测模型,因此,在检测理论的思维约束下,学者们很自然地推得传统的系统框架.下面探讨传统框架的优化可行性及途径.
梳理认知无线电网络中的几个既定事实:① 主用户开关状态随着时间变化缓慢,即其处于空闲状态的持续时间比较大;② 次用户的采样率比较高,可以在很短时间内获得一定的感知信息;③ 在有限的感知时间内,次用户存在不可忽略的检测错误率.
讨论1 认知无线电系统是否需要频谱感知以及参数重配置.首先,通过软件无线电平台,具备实现可行性.其次,通过较短时间内的频谱感知可以获取主用户的状态估计信息,虽然付出了感知时间的代价,但传输阶段内次用户发射功率会更加合理,所获得的平均信道容量会更大.当感知时间不断增大时,获取到的主用户状态估计信息增量带来的信道容量增益不断降低,当这2个效应迭加为0时,次用户的平均信道容量达到最大.因此,认知无线电系统需要频谱感知以及参数重配置.
讨论2 认知无线电系统是否需要频谱决策.首先,频谱决策将累积能量人为地进行二元化,并基于二元结果进行二元功率分配.直观地想,如果将功率分配直接定义在累积能量上,即将一个内外都是硬判决函数的复合函数定义为广义的非线性函数,那么其自由度和取值范围肯定更大.其次,累积能量越大,主用户存在的概率越小,为了减少对主用户的干扰,此时分配功率越小,因为累积能量是一个连续量,说明了分配的功率也相应地为连续量,而不是二元值.因此,认知无线电不需要频谱决策.
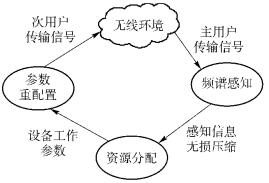
通过上面的分析,提出基于连续感知信息的认知无线电普适性框架,如图 2所示.其与传统框架不同的是,次用户不再进行频谱决策,也不存在频谱空洞的概念,而是根据获取的连续感知信息直接进行资源分配(包括功率分配).
|
图 2 提出的认知无线电普适性框架 |
在这里,连续感知信息可以通过无损的预处理,变换成其他参数,包括累积能量、主用户存在的概率、似然比等,不同的参数得到相同的系统性能,只是分析简便程度不一.为了简化分析,下面以累积能量为例,对提出的普适性框架进行数学建模,以进行定量分析.
2.2 连续功率分配下数学建模定义发射功率为累积能量x的函数为P(x),并满足非负约束P(x)≥0.在给定x时,次用户的瞬时信道增益在主用户空闲与存在时分别为
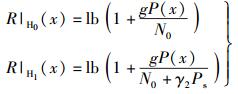
|
(6) |
则次用户的平均信道容量为

|
(7) |
其中f(x|H0)、f(x|H1)的定义如式(2) 所示.
对主用户产生的平均干扰可建模为

|
(8) |
考虑次用户本身的平均发射功率约束为
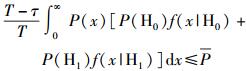
|
(9) |
则连续功率分配下,认知无线电普适性框架的数学建模为
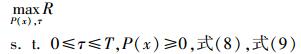
|
(10) |
通过在[0, T]上进行一维搜索,可得最优的τ.
可以证明,式(10) 为关于P(x)的凸优化问题.建立Lagrangian函数L(P(x), λ, μ)=R+λ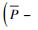

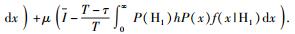
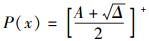
|
(11) |
其中:[x]+表示取0和x中的最大值,

|
(12) |
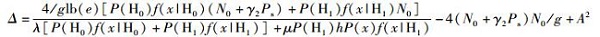
|
(13) |
采用梯度算法求解最优的λ和μ,通过迭代可以求得式(10) 的最优解.由于文中重点阐述框架的思想,同时受于篇幅的限制,这里就不再赘述,详细的求解可参考文献[6].
2.3 多电平功率分配下数学建模考虑2.2节中次用户采用离散发射功率的情况,即发射功率为累积能量x的分段函数Pm,满足非负约束Pm≥0.定义M+1个门限η0, η1, …, ηM,其中η0=0,ηM=+∞,当x∈[ηm-1, ηm)时,次用户分配功率Pm.
次用户在发射功率Pm下的瞬时信道增益为
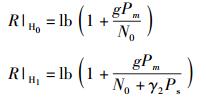
|
(14) |
次用户的平均信道容量为
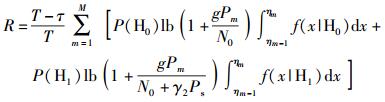
|
(15) |
次用户的平均发射功率约束和对主用户的平均干扰功率约束可以分别建模为
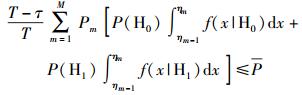
|
(16) |

|
(17) |
多电平功率分配下,认知无线电普适性框架的数学建模为
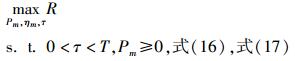
|
(18) |
式(18) 的求解可以参考2.2节以及文献[6],这里不再赘述.
3 几种框架的理论与数值比较3.1 理论分析与比较推论1 传统的3种认知无线电框架是提出的普适性框架的特殊情况.
证明 在式(10) 所示的连续功率分配下普适性框架中,分别代入下列参数,可以得到传统认知无线电框架的数学模型.设置P(x)为常数,代入τ=0,可得衬底式的数学模型;设置P(x)|x≤η为常数,代入P(x)|x > η=0,可得机会式频谱接入的数学模型;设置P(x)|x≤η和P(x)|x > η分别为常数,可得基于频谱感知频谱共享的数学模型.
在式(18) 所示的多电平功率分配下普适性框架中,分别代入下列参数,可以得到传统认知无线电框架的数学模型.代入τ=0和M=1,即可得到衬底式框架的数学模型;代入M=2和P2=0,即可得到机会式频谱接入框架的数学模型;代入M=2,即可得到基于频谱感知的频谱共享框架的数学模型.
推论2 提出的普适性框架信道容量不小于传统的3种认知无线电框架.这可直接从推论1得到.
提出的基于连续功率分配的普适性框架给出了系统性能的理论上限,而多电平功率分配提供了实际可行的方案.多电平功率分配的算法复杂度与传统的认知无线电框架处于同一数量级,并不会过多增加计算复杂度,而实际中,由于其离散性,可以以表的形式存储系统参数与发射功率的映射关系.
3.2 数值仿真分析与比较设置仿真参数为T=0.1s,Pdth=0.9,N0=1,fs=1kHz,I=0.1,P=Ps=10dB,P(H0)=0.7.
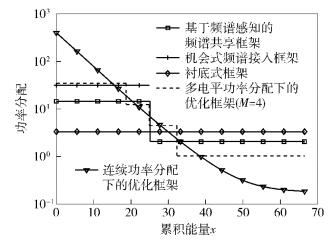
图 3所示为各框架中功率分配函数随着累积能量x的变化曲线.从图 3中可以看出,所提出的连续功率分配函数P(x)以及多电平功率分配函数Pm是关于累积能量x的非增函数.当x比较小时,P(x)比其他传统方法赋予更大的发射功率;而当x较大时,其分配的功率相对较小.多电平功率分配函数Pm可以看作是连续功率分配函数P(x)的离散化.
|
图 3 次用户发射功率关于累积能量的曲线 |
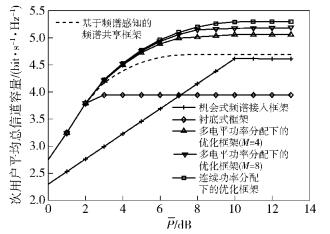
图 4所示为次用户平均信道容量关于平均发射功率约束P的变化曲线.从图 4中可以看出,当P较小时,所提出的框架与传统的框架具有相同的性能.但是当P变大时,所提框架在性能上得到了很大的改善.当P足够大时,所有算法得到的信道容量趋于平稳,这是因为该情况下,信道容量由I决定.图 4中可得,M=8的多电平功率分配下的框架性能与连续功率分配下的性能已经很接近,并且比传统的方法好很多.图 4证明了推论2.
|
图 4 次用户信道容量关于峰值发射功率的曲线 |
笔者提出了一种基于连续感知信息的认知无线电普适性框架,并考虑了连续功率分配和多电平功率分配2种情况.与传统认知无线电框架不同的是,所提出的框架不再对主用户是否存在进行二元判决,而是直接根据接收到的连续感知信息进行功率分配.理论分析表明,传统的3种认知无线电框架是提出的普适性框架的特殊情况,而数值仿真验证了框架性能的优越性.
| [1] | Gong Xiaowen, Vorobyov S A, Tellambura C. Optimal bandwidth and power allocation for sum ergodic capacity under fading channels in cognitive radio networks[J].IEEE Trans Signal Process, 2011, 59(4): 1814–1826. doi: 10.1109/TSP.2010.2101069 |
| [2] | Ding Guoru, Wang Jinlong, Wu Qihui, et al. Robust spectrum sensing with crowd sensors[J].IEEE Trans Commun, 2014, 62(9): 3129–3143. doi: 10.1109/TCOMM.2014.2346775 |
| [3] | Kang Xin, Liang Yingchang, Garg H K, et al. Sensing-based spectrum sharing in cognitive radio networks[J].IEEE Trans Veh Technol, 2009, 58(8): 4649–4654. doi: 10.1109/TVT.2009.2018258 |
| [4] | Chen Zhong, Wang Xiaodong, Zhang Xianda. Continuous power allocation strategies for sensing-based multiband spectrum sharing[J].IEEE J Sel Area Comm, 2013, 31(11): 2409–2419. doi: 10.1109/JSAC.2013.131126 |
| [5] | Chen Zhong, Gao Feifei, Zhang Zhengwei, et al. Multiple-level power allocation strategy in cognitive radio networks[J].Eurasia Journal on Advances in Signal Processing, 2014, 2014(15): 1–7. |
| [6] | Boyd S, Vandenberghe L. Convex optimization[M]. Cambridge: Cambridge Univ Press, 2003: 321-324. |


