为了在数字芯片上以低硬件复杂度实现Polar码的译码算法, 对Polar码连续消除(SC)译码算法接收符号和SC译码输入的初始比特对数似然比(LLR)的量化问题进行了研究.分析了接收符号量化区间和量化比特数对Polar码SC译码性能的影响.对译码输入初始LLR, 从均匀量化和非均匀量化两方面, 并对非均匀量化采用了归一化非均匀量化和小数非均匀量化2种方式, 分析了初始LLR的量化对Polar码SC译码性能的影响.仿真结果表明, 分别对接收符号和初始LLR采用区间[-4, 4]和区间[-20, 20]上的6bit均匀量化, 就可以使Polar码SC译码算法的误比特率(BER)性能损失小于0.1dB, 同时, 具有更简单的硬件实现复杂度.
In order to apply decoding algorithms of polar code in digital chips with low hardware complexity, the quantification problems on the received signals after channel transmission and the initial log likelihood ratios (LLR) of successive cancellation (SC) decoder were studied. The quantized interval and quantization accuracy for the received signals on system bit error rate (BER) performance were analyzed. For the quantization of initial LLR, both uniform and non-uniform quantization which contain two methods named normalizing quantization and decimal quantization were applied. Simulations show that 6 bit uniform quantization on interval [-4, 4] and [-20, 20] for received signals and initial LLR respectively can both bring BER performance loss less than 0.1dB, but with hardware implementation complexity decreased significantly.
香农在有噪信道编码理论[1]中指出,存在达到香农极限的码字. 2009年,Arıkan引入信道极化理论[2],提出Polar编码方案[3],实现了信道传输的最高传输速率并保证一定的传输可靠性.因Polar码具有在二进制离散无记忆信道上达到香农极限、译码算法复杂度低、时延小[4-6]等优点,在信源编码、协作中继以及干扰融合等各类通信领域中都具有重要的应用前景[7-9].
为在实际系统中应用信道编码,需对编码过程中的浮点型数据进行量化,但量化引入了数据失真,使得系统误比特率(BER, bit error rate)性能有一定的损失.为了降低这种BER损失,需要选取合适的量化参数.为此,孙蓉等[10-12]分别对Turbo码的最大后验概率译码算法、低密度奇偶校验码和准循环低密度奇偶校验码的置信传播译码算法的最优量化参数问题进行了研究.
在上述研究背景下,笔者分析了性能优良的Polar码连续消除(SC, successive cancellation)译码算法的量化问题,对Polar码经信道传输后的接收符号和输入SC译码器的初始比特对数似然比(LLR, log likelihood ratios)进行量化,分析了量化方式、量化取值范围以及量化精度等因素对系统误码性能的影响.
1 Polar码SC译码下的量化Polar码SC译码算法的量化框图如图 1所示.假设加性高斯白噪声(AWGN, additive white Gaussian noise)信道W:X→Y,X和Y分别为信道的输入和输出符号变量,信道转移概率定义为W(y|x), x∈X, y∈Y,且X中的x服从均匀分布,即符号是等概率发送的,则信道W的后验概率可表示为P(x|y)=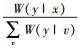
|
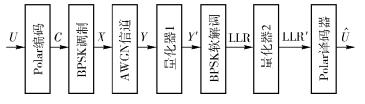
图 1 基于Polar码SC译码算法的量化框图 |
根据信道极化理论,对N=2n个独立信道W进行信道组合和信道分解后,可得到N个连续的二进制输入子信道WN(i), i=1, 2, …, N. Polar编码选择其中较为可靠的子信道来传输信源发出的信息比特,较不可靠的子信道用于传输冻结比特.其中冻结比特是具有固定值的比特,一般为0.记传送信息比特的子信道下标组成的集合为
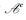


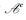
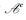

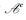


Polar码字比特序列c1N经过二进制相移键控(BPSK, binary phase shift keying)调制为符号x1N∈{-1, 1}N后,经由服从高斯正态分布N(0, σ2)的AWGN信道Z传输,得到输出符号y1N=x1N+z1N,z1N是噪声序列.接收端对信道输出符号y1N进行BPSK软解调,通过后验概率计算得到长度为N的初始LLR序列,对应LLR的计算公式可由LLR的定义推得

|
(1) |
其中:x(ci=0)=1, x(ci=1)=-1对应BPSK调制映射准则.
由于受信道噪声叠加的接收符号y1N是浮点型数据,故接收端BPSK软解调之前,先由图 1的量化器1将其量化为定点数据y′1N,再送入BPSK软解调,便可降低BPSK软解调模块的硬件实现复杂度.
对BPSK软解调输出的初始LLR序列进行SC译码时,由于初始LLR序列也是浮点型数据,故先由图 1中的量化器2将其量化为定点数据LLR′后,再进行SC译码,降低了SC译码器的实现复杂度.
由Polar码信道组合和拆分的理论可知,SC译码路径度量与已知y1N时的后验概率PN(i)(u1i|y1N)有关,与信道组合的信道转移概率表达式一样,后验概率也可由迭代计算得到.假设u1, oj和u1, ej分别代表子向量u1j奇数下标和偶数下标的元素,则对任意n≥0,由后验概率表示的Polar码SC译码路径度量公式为
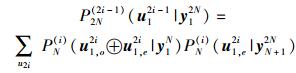
|
(2) |

|
(3) |
为便于计算,采用后验概率LLR来代替式(2) 和式(3) 中的后验概率,并将BPSK软解调输出的初始比特LLR序列记作第(n+1) 层LLR序列λ(n+1)={λ1(n+1), λ2(n+1), …, λN(n+1)},则Polar码SC译码的路径度量式(2) 和式(3) 可简化为
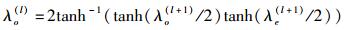
|
(4) |
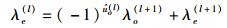
|
(5) |
其中:λo(l)和λe(l)分别为第l(1≤l≤n)层LLR序列中奇数位置和偶数位置上的元素值,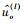



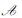
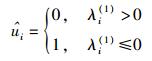
|
(6) |
图 1中量化器1对接收符号Y进行均匀量化时,先将Y在其量化区间内等间隔分割,形成不同的均匀子分割区间,再用各子分割区间的中值作为该子区间上所有浮点型数值的近似值,其中量化间隔由量化比特数决定.
对接收符号Y的量化区间的选取,可由Y的取值分布,即Y的累积概率分布函数来确定.对图 1所示的Polar码BPSK调制系统,当BPSK调制符号等概发送,即

|
(7) |
其中y0为任一实常数.对式(7) 求导,即得接收符号Y的概率密度函数为
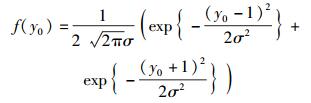
|
(8) |
根据高斯变量分布的“3σ准则”可知[13],Y以大于99.73%的概率分布在区间[-1-3σ, 1+3σ],其中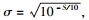
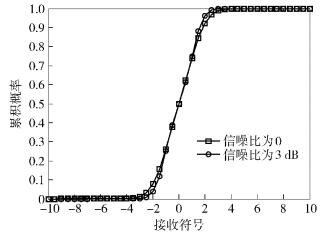
下面基于图 1的仿真都假设系统中Polar码的码长N=210,码率R=0.5.图 2为在系统的发射信噪比分别为0和3dB时,由接收符号Y的累积概率分布式(7) 得到的累积概率分布曲线.由图 2可知,不同发射信噪比下,接收符号Y的取值几乎都落在[-4, 4]区间内,故接收符号Y的量化区间可以选为[-4, 4],这与“3σ准则”的计算结果是一致的.
|
图 2 接收符号Y的累积概率分布 |
为了考查接收符号Y在不同区间上的量化对Polar码SC译码算法BER性能的影响,在图 1的量化器1中对接收符号Y分别进行了区间[-3, 3]、[-4, 4]和[-5, 5]上的8bit均匀量化,并将量化后的Y′送入BPSK软解调器和SC译码器,得到Polar码在只有量化器1时的SC译码算法BER曲线,如图 3所示.

|
图 3 接收符号Y的8bit均匀量化BER曲线 |
从图 3中可以看出,与未量化时相比,对接收符号Y在[-3, 3]区间上进行8bit均匀量化时,Polar码SC译码的BER性能在整个信噪比区间上都有一定的损失,在BER为10-2时达到最大值0.15dB;而在[-5, 5]区间上的量化则只在大于2.5dB的较高信噪比区间上,出现了明显的BER损失,在BER为3×10-4时达到最大值0.12dB.当接收符号Y在[-4, 4]区间上进行8bit均匀量化时,BER性能几乎没有损失.可见,在Polar码SC译码算法下,对接收符号Y在区间[-4, 4]上的量化可以在降低BPSK软解调器硬件实现复杂度的同时引入较小的BER性能损失.这主要是由于接收符号Y的取值集中分布在区间[-4, 4]上,更大或更小的量化区间由于量化误差的增加都不会带来性能上的提高.
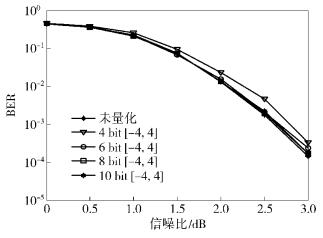
为了考查接收符号Y的量化比特数即量化精度对Polar码SC译码算法BER性能的影响,图 4给出了量化区间为[-4, 4],量化比特数分别为4、6、8、10时,Polar码SC译码算法的BER性能曲线.
|
图 4 接收符号Y在[-4, 4]区间上均匀量化BER曲线 |
由图 4可以看出,与未量化时相比,4bit的均匀量化引起的BER损失较大,在5×10-2时达到最大约0.25dB;6bit量化只在较高信噪比区域上,引起了约0.1dB的BER性能损失;8bit和10bit量化的BER性能几乎没有损失.可见,量化比特数越大,系统的BER性能损失越小.为减少硬件实现的复杂度,6bit均匀量化更为合适.
2.2 SC译码器输入初始LLR的量化2.2.1 均匀量化对初始LLR均匀量化区间的选取同样可由其累积概率分布函数来确定.由式(1) 的初始LLR计算公式可推出初始LLR的累积概率分布函数为
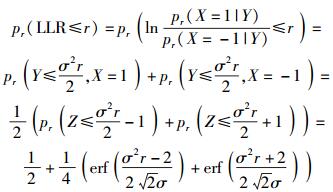
|
(9) |
其中r为任一常数.对式(9) 求导,可得初始LLR的概率密度函数为
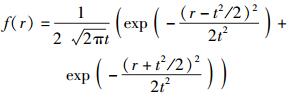
|
(10) |
其中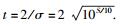
同样,由高斯变量分布的“3σ准则”可知,初始LLR以大于99.73%的概率分布在区间[-t2/2-3t, t2/2+3t]上.由累积概率分布式(9) 得到的发射信噪比分别为0和3dB时,初始LLR的累积概率分布曲线如图 5所示.由图 5可以看到,在不同发射信噪比下的初始LLR取值几乎全部落在[-20, 20]区间内,即初始LLR的量化区间可选为[-20, 20],这与“3σ准则”的理论计算结果是一致的.

|
图 5 译码输入初始LLR累积概率分布 |
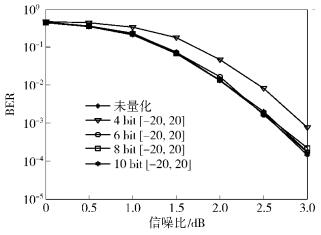
图 6和图 7给出了量化区间分别为[-20, 20]和[-40, 40],量化比特数分别为4、6、8和10时,Polar码SC译码算法在只有量化器2时的BER性能曲线.
|
图 6 初始LLR在[-20, 20]区间上的量化BER曲线 |
|
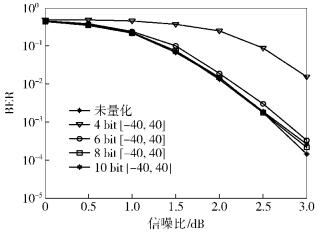
图 7 初始LLR在[-40, 40]区间上的量化BER曲线 |
对比图 6与图 7可知,与未量化时相比,相同量化比特数时,初始LLR在[-40, 40]区间上均匀量化引起的BER性能损失均大于在区间[-20, 20]上对应量化比特数的均匀量化.可见,Polar码SC译码初始LLR的量化区间选为[-20, 20]更合适.
由图 6还可以看出,与未量化时相比,区间[-20, 20]上的4bit均匀量化引起的BER性能损失较大,在10-3时达到最大约0.4dB;而在大于等于6bit的量化时,BER性能几乎没有损失.因此,对初始LLR选择[-20, 20]区间上的6bit均匀量化可兼顾较低的硬件实现复杂度和较小的译码性能损失.
2.2.2 非均匀量化为了考查初始LLR的非均匀量化对Polar码SC译码算法BER性能的影响,对图 1的量化器2应用了A律和μ律2种压扩函数,且对应的压扩函数分别为

由压扩函数式可知,A律和μ律非均匀量化的作用区间都在(0, 1]上,而由图 5的LLR累积概率分布可知,LLR的取值大部分集中在区间[-20, 20]上.因此,在对初始LLR进行非均匀量化之前,需先将初始LLR的取值区间转换到(0, 1]上.为此,采用了2种区间转换的办法.一种是先计算初始LLR绝对值的上取整数值,再用实际的初始LLR值除以该整数,得到数值小于1的归一化初始LLR,对其进行非均匀A律和μ律量化后,再乘以该上取整数,得到最终的定点型数据LLR′,记这种量化方式为归一化非均匀量化.另一种是只对初始LLR的小数部分应用非均匀A律和μ律量化,并用量化后的小数代替原初始LLR中的小数部分,得到最终的定点型数据LLR′,记这种量化方式为小数非均匀量化.无论采用哪种量化方式,量化得到的定点型数据LLR′都将送入SC译码器进行迭代译码.
图 8和图 9分别给出了量化器2采用非均匀A律和μ律量化时,SC译码算法的BER性能曲线.曲线A和曲线μ对应归一化非均匀量化,曲线A-和曲线μ-对应小数非均匀量化.

|
图 8 非均匀A律量化下的BER曲线 |

|
图 9 非均匀μ律量化下的BER曲线 |
由图 8可以看到,与未量化时相比,初始LLR的归一化A律量化只在高信噪比区域上引起了最大约0.2dB的性能损失;而小数A律量化的BER性能损失在全信噪比区间上都小于0.1dB.可见,小数A律量化可以使Polar码SC译码的BER性能在更大的信噪比范围上接近未量化系统的BER性能,且BER性能损失不超过0.1dB.由图 9可以看到,归一化μ律量化下Polar码SC译码的BER性能在整个信噪比区域上,都介于未量化系统和采用了小数μ律量化系统之间,即归一化μ律量化方式下的系统BER性能可以在更大程度上接近未量化时系统的BER性能.
将初始LLR在均匀量化和非均匀量化2种量化方式下系统的BER性能进行对比,得到图 10.

|
图 10 均匀和非均匀量化下的BER曲线 |
由图 10可以看到,[-20, 20]区间上的6bit均匀量化对应的Polar码SC译码算法的BER性能在整个信噪比区域上都比非均匀量化更接近未量化时系统的BER性能.同时,均匀量化的算法简单,在硬件实现上也比非均匀量化的复杂度更低.因此,对BPSK软解调输出初始LLR的量化,更宜采用[-20, 20]区间上的6bit均匀量化.
3 结束语针对Polar码SC译码算法的定点实现问题进行了分析和讨论.研究了接收符号的量化区间和量化比特数对Polar码SC译码性能的影响.应用均匀量化和非均匀量化2种量化方式对译码输入初始LLR的量化进行了分析,且非均匀量化采用了归一化量化和小数量化2种方式.仿真结果表明,对接收符号和初始LLR的最佳量化方式是[-4, 4]区间和[-20, 20]区间上的6bit均匀量化.
| [1] | Shannon C E. A mathematical theory of communication[J].Bell System Technical Journal, 1948, 19(4): 271–285. |
| [2] | Arıkan E. Channel combining and splitting for cutoff rate improvement[J].IEEE Trans Inf Theory, 2006, 52(2): 628–639. doi: 10.1109/TIT.2005.862081 |
| [3] | Arıkan E. Channel polarization: a method for constructing capacity achieving codes for symmetric binary-input memoryless channels[J].IEEE Trans Inf Theory, 2009, 55(7): 3051–3073. doi: 10.1109/TIT.2009.2021379 |
| [4] | Wu Daolong, Li Ying, Sun Yue. Construction and block error rate analysis of polar codes over AWGN channel based on gaussian approximation[J].IEEE Communications Letters, 2014, 18(7): 1099–1102. doi: 10.1109/LCOMM.2014.2325811 |
| [5] | Niu Kai, Chen Kai. Stack decoding of polar codes[J].Electronics Letters, 2012, 48(12): 695–697. doi: 10.1049/el.2012.1459 |
| [6] | Niu Kai, Chen Kai. CRC-aided decoding of polar codes[J].IEEE Communications Letters, 2012, 16(10): 1668–1671. doi: 10.1109/LCOMM.2012.090312.121501 |
| [7] | Hussami N, Korada S B, Urbanke R. Performance of polar codes for channel and source coding[C]//2009 IEEE International Symposium on Information Theory (ISIT 2009). Seoul: IEEE Press, 2009: 1488-1492. |
| [8] | Goela N, Abbe E, Gastpar M. Polar codes for broadcast channels[C]//2013 IEEE International Symposium on Information Theory(ISIT 2013). Istanbul: IEEE Press, 2013: 1127-1131. |
| [9] | Appaiah K, Koyluoglu O O, Vishwanath S. Polar alignment for interference networks[C]//49th Annual Allerton Conference on Communication, Control, and Computing (AACCCC2011). Monticello: IEEE Press, 2011: 240-246. |
| [10] |
孙蓉, 陈军, 邓浩, 等. Turbo码MAP译码算法中量化问题的研究[J]. 电子学报, 2001, 29(10): 1356–1359.
Sun Rong, Chen Jun, Deng Hao, et al. Study on some quantification issues for decoding of Turbo codes with MAP algorithm[J].Acta Electronica Sinica, 2001, 29(10): 1356–1359. doi: 10.3321/j.issn:0372-2112.2001.10.015 |
| [11] |
孙韶辉, 孙蓉, 王新梅. 低密度校验码BP译码算法中量化问题的研究[J]. 电子学报, 2003, 31(2): 217–220.
Sun Shaohui, Sun Rong, Wang Xinmei. Some quantization issues for decoding of low-density parity check codes with BP algorithm[J].Acta Electronica Sinica, 2003, 31(2): 217–220. |
| [12] |
徐志江, 胡冰璞, 张江鑫. 基于BP译码算法的准循环低密度奇偶校验码量化问题研究[J]. 浙江工业大学学报, 2014, 42(3): 260–264.
Xu Zhijiang, Hu Bingpu, Zhang Jiangxin. The research on quantization issues of quasi-cycle low-density parity check codes based on BP algorithm[J].Journal of Zhejiang University of Technology, 2014, 42(3): 260–264. |
| [13] |
姚如贵, 尹武涛, 王永生. LogMAP译码算法量化方法研究[J]. 计算机仿真, 2008, 25(12): 351–354.
Yao Rugui, Yin Wutao, Wang Yongsheng. Quantification techniques of LogMAP decoding algorithm[J].Journal of Computer Simulation, 2008, 25(12): 351–354. doi: 10.3969/j.issn.1006-9348.2008.12.088 |


