提出一种改进的基于l0范数的最小均方(LMS)算法.采用误差的相关函数值调整权系数步长因子以及零吸引项, 增强系统的抗噪声性能; 引入一种修正的权系数步长因子更新方法, 进而使系统具有较快的跟踪速度.对提出的算法进行理论分析, 在不同信噪比下进行仿真验证, 并与已有的基于l0范数的LMS算法进行比较.理论分析结合仿真验证都表明, 新提出算法具有较快的跟踪速度和较强的抗噪声性能.
A new variable step-size l0_least mean square (LMS) algorithm is proposed. A step size control method and the zero attraction items reweight method based on correlation function value of the error to increase the convergence speed, and reduce the steady-state misalignment. The anti-noise performance, convergence, tracking steady state error and misadjustment of this algorithm are discussed in theoretical analysis. Finally, the algorithm is compared with l0_LMS and Il0_LMS in different signal-to-noise ratio. Theoretical analysis combined with experimental simulation conclusion: the algorithm can achieve better tracking speed, lower steady state error and anti-noise performance.
最小均方(LMS, least mean square)算法在系统识别、自适应控制、信道均衡等领域[1-5]广泛应用.传统的LMS不具备稀疏性,然而实际中的系统大都具有稀疏性.针对此,谷源涛等[6]将l0范数引入到传统的LMS代价函数中.有关l0范数约束算法的收敛性问题,Su等[7]进行了讨论分析. l0_LMS算法是传统LMS算法上的改进,虽使算法性能得到一定的提高,但仍受随机梯度噪声的影响,不能同时兼顾快速收敛和小的稳态失调量;当l0_LMS算法过程趋于稳定状态时,由于对零点附近的小系数加权了过大系数,导致算法的失调量变大.鉴于此,曲庆等[8]给出了Il0_LMS算法,但此算法中误差也易受噪声干扰且权系数调整步长因子还待修正.针对此,笔者提出一种改进的l0_LMS算法,理论分析并结合仿真表明,此算法相比l0_LMS和Il0_LMS都具优越性.
1 算法及分析1.1 算法阐述传统LMS算法不具备稀疏性,但现实中的系统大多具备稀疏性,这就促进对传统LMS算法的改进.在传统LMS算法中引入l0范数,可加速收敛稀疏系统中的非零系数[6]. l0_LMS算法异于传统LMS算法的主要一点是把传统LMS算法的约束函数修改成2项之和:误差二次方加上滤波器权矢量的l0范数,公式表示为
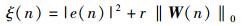
|
(1) |
其中:e(n)为误差信号, r为常数,W(n)为滤波器的权矢量,‖· ‖0表示l0范数.此时W(n)的更新式为
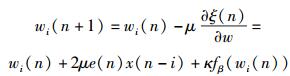
|
(2) |
其中:0≤i < L,L为滤波器阶数;μ为步长且0 < μ < 1/(λmax),β为展开系数,λmax为R=[X(n) XT(n)]的最大特征值;κ=μ×r为约束项和估计误差之间的平衡因子;fβ(wi(n))为
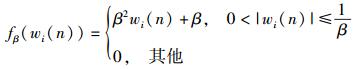
|
(3) |
由于随机梯度噪声会直接影响l0_LMS算法的性能,使得不同兼顾快速收敛和小稳态误差;同时又对零点附近的小系数加权了过大系数,导致算法的稳态失调量变大。鉴于以上问题,曲庆等[8]提出了Il0_LMS算法.
该算法思想是利用误差信号e(n)和收敛程度之间的关联,进而通过误差信号e(n)控制μ的变化,具体见式(4)~(5).
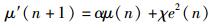
|
(4) |
其中α和χ为步长调整因子.
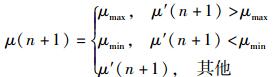
|
(5) |
通过估计误差信号e(n)和收敛程度之间的关联修正零吸引项,修正后的权系数迭代方程为
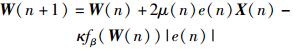
|
(6) |
分析Il0_LMS可知,此算法抗噪声性能有待改进,且跟踪速度以及稳态失调量也需进一步修正.为此笔者用误差的相关函数值调整权系数步长以及零吸引项,增强系统的抗噪声性能,且引入一种修正的权系数步长因子更新方法,进而得到较快的跟踪速度.
笔者提出的算法具体表示为
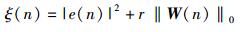
|
(7) |
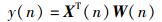
|
(8) |
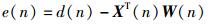
|
(9) |
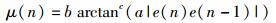
|
(10) |
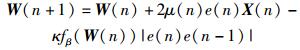
|
(11) |
其中a、b和c都是大于0的数.
1.2 算法性能分析1) 抗噪声性能
根据笔者给出的算法,由式(9) 得
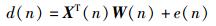
|
(12) |
又有
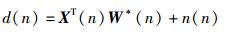
|
(13) |
其中:n(n)为高斯随机白噪声,与输入信号x(n)相互独立;W*(n)为自适应滤波的最优权矢量.
令系数偏移矢量为
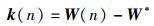
|
(14) |
由式(12)~(14) 得
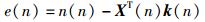
|
(15) |
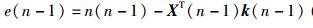
|
(16) |
则有
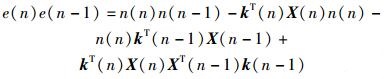
|
(17) |
故有
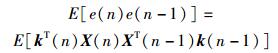
|
(18) |
由式(18) 可知,E[e(n)e(n-1)]不受噪声n(n)的影响.故用e(n)e(n-1) 调整μ(n)或W(n)时,能提高算法的抗噪声性能;用e(n)e(n-1) 对W(n)进行零吸引项校正时适应性比较强. k(n)趋于零矢量时,n(n)n(n-1) 决定着e(n)e(n-1) 的变化,但n(n)和n(n-1) 独立无关,故n(n)n(n-1) 对稳态步长的影响会很小,故用e(n)e(n-1) 调节权系数的变化可减少噪声的干扰,使得最终稳态失调较小.
2) 收敛性与稳态误差分析
结合式(11) 和式(13)~(15),可得
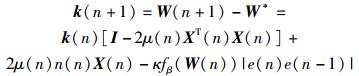
|
(19) |
式(19) 两边同时求期望,可得
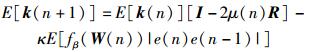
|
(20) |
其中R=E[XT(n)X(n)]为X(n)的自相关函数.对R进行特征值分解,表示为R=QΛQT,Λ=diag[λ1, λ2, …, λL]为由R的特征值组成的矩阵,Q=diag[q1, q2, …, qL]为对应特征值的特征向量.
假设
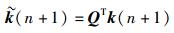
|
(21) |
结合式(20) 和Q=diag[q1, q2, …, qL],可得
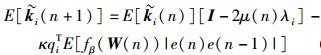
|
(22) |
当n→∞时,E[|e(n)e(n-1)|]→ε, ε值很小.另外,qiTE[fβ(W(n))]是有界的[7, 9].故式(20) 是收敛的,可得
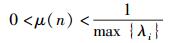
|
(23) |
依据式(19),可得
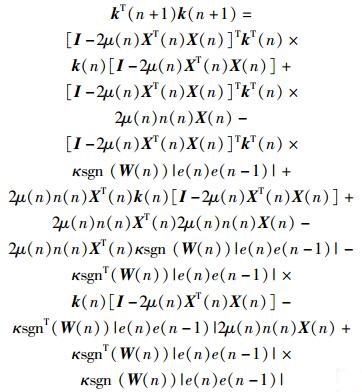
|
(24) |
假设
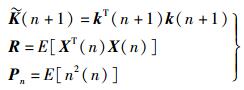
|
(25) |
对式(24) 两边取期望并两端取迹得
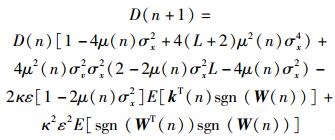
|
(26) |
其中σx2和σv2分别为输入信号和噪声的功率.由式(26) 可得一个修正的收敛条件为
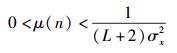
|
(27) |
结合式(22)、式(23) 和式(27) 可得
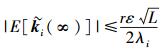
|
(28) |
所以得到很小的稳态误差值.
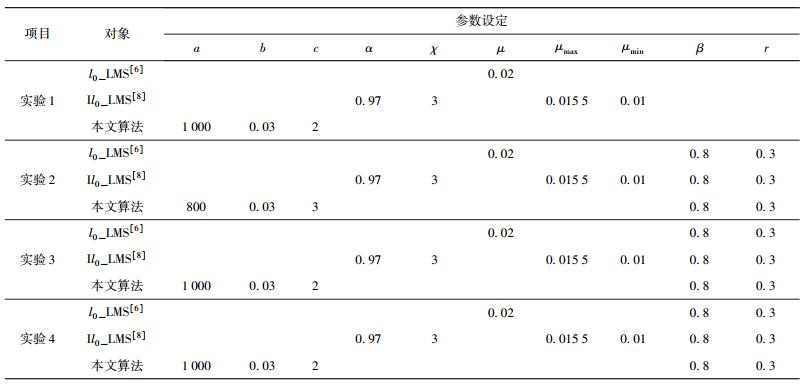
2 算法性能仿真分析为了说明本文算法的性能,设计4组实验.第1组是比较l0_LMS[6]、Il0_LMS[8]和本文算法的步长变化,用来说明本文算法跟踪速度快、稳态误差小.第2组和第3组是分别在输入高低信噪比下不相关的信号时,比较l0_LMS[6]、Il0_LMS[8]和本文算法,用来说明本文算法的跟踪速度快和抗噪声能力好;第4组是输入相关的信号,比较l0_LMS[6]、Il0_LMS[8]和本文算法,验证本文算法在跟踪速度和抗噪声性能方面依然都好于其他2种.
|
|
表 1 实验参数的设定 |
|
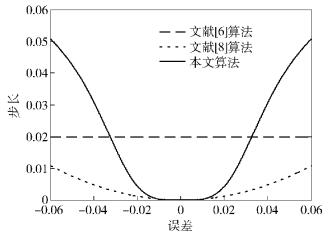
图 1 算法的步长比较 |
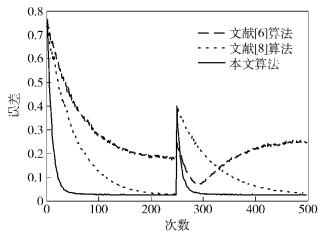
实验2 输入信噪比为30dB的不相关信号,采样点为500,实验过程中在第250个采样点处系统发生改变.独立重复2000次实验.实验中的参数设置见表 1,仿真结果如图 2所示.
|
图 2 信噪比为30dB时误差曲线比较 |
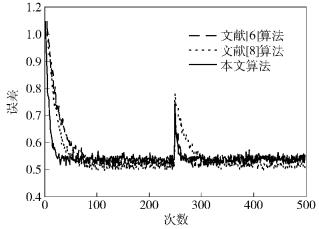
实验3 输入信噪比为13dB的不相关信号,采样点为500,实验过程中在第250个采样点处系统发生改变.独立重复2000次实验.实验中的参数设置见表 1,仿真结果如图 3所示.
|
图 3 信噪比为13dB时误差曲线比较 |
实验4 输入信噪比为13dB的相关信号,采样点为500,实验过程中在第250个采样点处系统发生改变.独立重复2000次实验.实验中的参数设置见表 1,仿真结果如图 4所示.
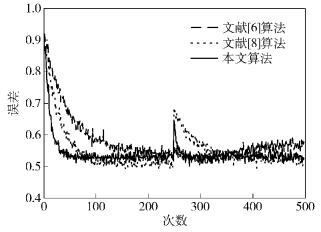
|
图 4 信噪比为13dB时相关信号误差曲线比较 |
由图 1可知,本文算法相比l0_LMS[6]和Il0_LMS[8],权系数调整步长μ(n)变化趋势与误差e(n)一致.进一步可知,在初始阶段e(n)较大,则对应会有较大且变化迅速的μ(n),使得算法有较快的收敛速度;在算法趋于稳定时,e(n)较小,μ(n)较小且平缓,进而使得系统产生较小的稳态误差.由图 2和图 3可知,当系统输入非相关信号时,不论输入信号的信噪比是低还是高,本文算法相比l0_LMS[6]和Il0_LMS[8],不仅跟踪速度快且稳态误差小.由图 4可知,当输入低信噪比的相关信号时,本文算法相比l0_LMS[6]和Il0_LMS[8],同样有大的跟踪速度和小的稳态误差.
3 结束语为了增加稀疏系统的跟踪速度以及抗噪声性能,通过利用误差的相关函数来控制权系数调整步长和零吸引项,提出了新的改进l0_LMS算法.通过理论分析和试验比较得到,提出的算法不仅跟踪速度快,而且稳态失调量小并有较好的抗干扰性能.
| [1] | Wu Feiyun, Tong Feng. Non-uniform norm constraint LMS algorithm for sparse system identification[J].IEEE Communications Letters, 2013, 17(2): 385–388. doi: 10.1109/LCOMM.2013.011113.121586 |
| [2] | Kalouptsidis N, Mileounis G, Babadi B, et al. Adaptive algorithms for sparse system identification[J].Signal Processing, 2011, 91(8): 1910–1919. doi: 10.1016/j.sigpro.2011.02.013 |
| [3] | Zhao Shengkui, Man Zhihong, Khoo Suiyang, et al. Variable step-size LMS algorithm with a quotient form[J].Signal Processing, 2009, 89(1): 67–76. doi: 10.1016/j.sigpro.2008.07.013 |
| [4] |
田福庆, 罗荣, 李克玉, 等. 基于改进的双曲正切函数变步长LMS算法[J]. 系统工程与电子技术, 2012, 34(9): 1758–1706.
Tian Fuqing, Luo Rong, Li Keyu, et al. New variable step-size LMS algorithm based on modified hyperbolic tangent function[J].Systems Engineering and Electronics, 2012, 34(9): 1758–1706. |
| [5] | Costa M H, Bermudez J C M. A noise resilient variable step-size LMS algorithm[J].Signal Processing, 2008, 88(3): 733–748. doi: 10.1016/j.sigpro.2007.09.015 |
| [6] | Gu Yuantao, Jin Jian, Mei Shunliang. l0 norm constraint LMS algorithm for sparse system identification[J].IEEE Signal Processing Letters, 2009, 16(9): 774–777. doi: 10.1109/LSP.2009.2024736 |
| [7] | Su Guolong, Jin Jian, Gu Yuantao, et al. Performance analysis of l0 norm constraint least mean square algorithm[J].IEEE Transactions on Signal Processing, 2012, 60(5): 2223–2235. doi: 10.1109/TSP.2012.2184537 |
| [8] |
曲庆, 金坚, 谷源涛. 用于稀疏系统辨识的改进l0_LMS算法[J]. 电子与信息学报, 2011, 33(3): 604–609.
Qu Qing, Jin Jian, Gu Yuantao. An improved l0_LMS algorithm for sparse system identification[J].Journal of Electronics and Information, 2011, 33(3): 604–609. |
| [9] | Jin Jian, Qu Qing, Gu Yuantao. Robust zero-point attraction least mean square algorithm on near sparse system identification[J].IET Signal Processing, 2013, 7(3): 210–218. doi: 10.1049/iet-spr.2012.0125 |