2. 电信科学技术研究院 无线移动通信国家重点实验室, 北京 100191
针对下行多输入多输出-正交频分复用(MIMO-OFDM)系统, 提出了在总功率限制和用户比例公平性约束下, 使系统能量效率最大化的资源分配算法.为了降低计算复杂度, 提出了两步优化的次优子载波和功率分配算法.第1步由子载波共享和平坦衰落假设得到估计的能效发射功率, 并采用等功率分配方法完成子载波分配; 第2步在子载波分配基础上完成能效最优的功率分配.仿真结果表明, 所提算法以较低的复杂度逼近最优算法的性能, 并且在保证用户比例公平性的同时可带来明显的能效提升.
2. State Key Laboratory of Wireless Mobile Communications, China Academy of Telecommunications Technology (CATT), Beijing 100191, China
An energy efficient resource allocation algorithm for downlink multiple-input-multiple-output orthogonal frequency division multiple (MIMO-OFDM) system was proposed to implement the energy efficiency (EE) maximization, satisfying total power constraint as well as the proportional rate constraints. In order to reduce the computational complexity, a two-step subcarrier assignment and power allocation scheme was proposed to derive the suboptimal solution of the optimization problem. The estimated energy-efficient transmit power is obtained under assumption of flat fading and subcarrier sharing. The equal-power allocation-based method was adopted to carry out subcarrier assignment. Furthermore, the optimal energy-efficient power allocation was derived according to the result of the first-step subcarrier assignment. Simulations show that the proposed algorithm brings remarkable gains on energy efficiency and guarantees proportional fairness of the users.
多输入多输出(MIMO, multiple input multiple output)和正交频分复用(OFDM, orthogonal frequency division multiple)技术为第4代移动通信系统(4G)的关键技术,二者的结合能够进一步提高系统容量或性能.然而,随着无线网络中高速数据业务的指数式增长,网络的能量消耗显著增加.绿色通信及无线网络的能效设计成为未来移动通信的一大挑战[1].
MIMO和OFDM系统中的资源分配问题已经被广泛研究[2-3].近两年,人们开始关注OFDM和MIMO系统中的能效资源分配问题[4-5]. Ren等[4]在比例速率限制下提出了在OFDM系统下低复杂度的能效资源分配算法. Zhao等[5]对下行MIMO系统能效最优的功率分配进行了理论分析,证明了单数据流和多数据流传输下系统存在全局最优能效,但是没有给出多用户MIMO-OFDM系统下用户速率限制下的联合资源分配.笔者研究文献[6]中的能效问题,但与文献[7]中的基于统计用户服务质量(QoS, quality of service)约束下的能效资源不同,关注在比例速率限制下的能效资源分配算法,使用凸优化方法设计了低复杂度的迭代算法.
1 系统模型考虑由K个用户组成的时分双工(TDD, time division duplex)下行多用户MIMO-OFDM系统,其中基站配置Nt根天线,每个用户配置Nr根天线.系统带宽为B,且等分为N个子载波.假设在整个带宽内,MIMO-OFDM信道为频率选择性衰落.假设OFDM循环前缀(CP, cyclic prefix)长度大于最大时延扩展,从而每个子载波互不干扰,因此在每个子载波上服从平坦衰落.令用户k在子载波n上的信道系数矩阵为

|
(1) |
其中: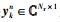
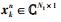

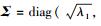
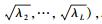

|
(2) |
定义整型变量ρk, n来表示子载波分配情况,如果子载波n分给了用户k,则ρk, n=1,否则为0.且用户间不能共享子载波,ρ=[ρk, n]K×N代表一个可行子载波分配指示矩阵,满足以下约束条件
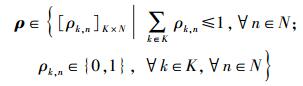
|
(3) |
由香农公式可得用户k的速率为
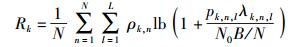
|
(4) |
其中N0为噪声功率.
1.1 问题描述与传统MIMO-OFDM系统最大化频谱效率不同,笔者以最大系统能效为目标,并保证用户QoS要求前提下的联合子载波、功率分配.假设系统的功率消耗由电路消耗功率和发射机发射功率2个部分组成,即PTrans=ζPT+PC.其中:ζ为功放放大效率因子,Pt为基站发射功率,PC为电路的功率消耗,这里假设为固定常数.
能效(EE, energy efficiency)是指每单位能量所传输的比特数,因此,能效可以表示为
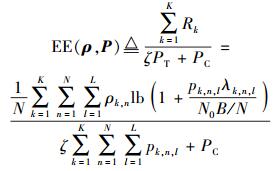
|
(5) |
因此,能效优化问题的数学模型可以表示为
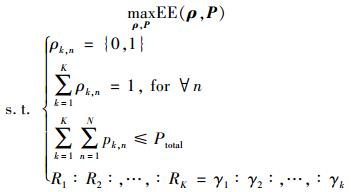
|
(6) |
式(6) 优化问题中存在非线性限制条件及整数变量,是一个复杂的非凸问题,因此联合优化子载波、功率的优化算法复杂度高,实现起来比较困难.因此提出分离的资源分配算法,子载波分配及功率分配.
2 能效资源分配算法2.1 次优子载波分配高能效传输的目标是最大化每单位能量的传输比特数,式(5) 中分母中的发射功率可能会低于总功率.而最大化频谱效率通常是满功率发射以使系统吞吐量最大化.因此在最优的能效功率分配时,给定的子载波分配是否为能效最优的子载波分配是考虑的重点问题.这里采用以下2步完成基于能效的子载波分配:
1) 基于能效的发射功率估计;
2) 估计发射功率下子载波分配.
这2步很难得到最优解,因此使用2个次优的方法来代替.
1) 基于能效的发射功率估计
子载波共享和平坦衰落的概念在多载波系统中子信道分配中应用广泛[9].类似地,假设子载波是共享的,用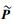
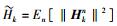
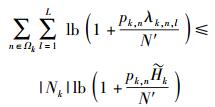
|
(7) |
其中:N′=N0B/N,Ωk是分配给用户k的子载波集合;|Nk|是子载波分配的个数.用户k的速率可以表示为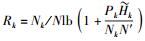

|
(8) |
引入速率参数
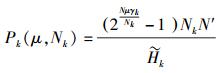
|
(9) |
因此能效优化问题已经转化为在给定μ下的功率最小化问题.定义一个以μ为自变量的最小功率消耗函数

|
(10) |
显然用户的功率随着Nk是单调递减的,当所有子载波都分完的功率消耗是最小的.由于



|
(11) |
其中θ为非负拉格朗日乘子.则由KKT条件得

|
(12) |
因此,最优的子载波分配Nk是满足式(12) 的非线性等式方程的根.定义θk(Nk)为

|
(13) |
对式(13) 进行求导得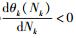


|
(14) |
由此得最小功率算法流程如下:
① 根据式(14) 设定θ的初始值.
② 令qtemp=(q1+qu)/2根据二分法得到满足比例速率要求的子载波分配{Nk}k∈K.
③ 判断
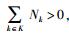
④ 重复步骤②、③,直到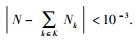
现在将能效问题改写为

|
(15) |
由于式(15) 中分母是严格凸的,分子凹的,因此新的能效函数是严格拟凹的,因此存在唯一的最优解使能效最大化.对于拟凹的分式优化问题使用参数法求解[11],将式(15) 问题写成如下减式

|
(16) |
由于式(15) 能效函数是严格拟凹的,存在唯一的最优解q*使得式(16) 最大,且满足q=q*⇔F(q)=0.这说明了求解式(15) 中最大的能效问题等价于寻找非线性等式方程的根.
基于能效的功率估计可由2层循环来完成,外层循环可采用二分法求得最优的辅助参数q*,内层循环完成最小功率分配.能效功率估计算法流程如下.
① 设定初始点q1=0,qu使得F(qu) < 0.
② 令qtemp=(q1+qu)/2,计算F(qtemp),使用二分法和最小功率算法求得qtemp下最优的μtemp*、最优的子载波分配及总消耗功率.代入F(qtemp)后进行下一步判断.
③ 如果F(qtemp) > 0,q1=qtemp,否则qu=qtemp.
④ 重复步骤②、③,直到|F(qtemp)| < 10-4,在此得到最优的μ*,因此得到估计的功率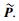
2) 估计发射功率下子载波分配
由1) 得到的估计功率,进行次优的子载波分配.采用等功率分配方法,利用最大特征值来代替整个信道增益完成子载波分配[12].
2.2 确定子载波下的最优功率分配在给定子载波分配后,可以得到最优的功率分配.通过引入一个辅助变量简化比例速率限制条件.得到转化后的能效优化问题,新的分式优化可以通过参数法求解.
对于窄带点对点MIMO,最优的功率可以通过空间子信道注水得到.在多用户多载波MIMO-OFDM系统,假设用户k分到的子载波集合为Ωk.使系统容量最大化的最优功率分配是在分配的子载波上执行空频二维功率注水.然而,基于能效的功率分配是在满足用户速率要求下使发射功率最小.因此可以得到用户k的能效功率分配

|
(17) |
其中:[x]+=max(x, 0);μ为满足速率限制的拉格朗日乘子.令Pk(Rk|Ωk)代表用户k的功率消耗

|
(18) |
对于多用户功率分配,最优的功率分配应该满足比例速率限制,因此,引入一个辅助变量β,有

|
(19) |
由此得到总发射功率为

|
(20) |
显然,发射功率随着β增加,存在βmax使得PT(βmax)=Ptotal.因此将能效优化问题变换为
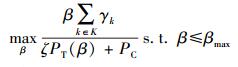
|
(21) |
式(21) 与式(15) 一样是严格拟凹的.通过式(22) 将非线性分式优化转化为线性的拟凹的分式优化问题, 同样地对式(22) 使用参数法求解.

|
(22) |
最优功率分配算法过程如下.
① 设置q1=0,qu»0,满足F(qu) < 0.设置βlow=0,βhigh则通过在所分配子载波上注水所得容量与比例速率限制条件比值的最大值.再通过二分法求得满足PT(βmax)=Ptotal的βmax.
② 更新qtemp=(q1+qu)/2,在qtemp、βlow和βmax下求解问题(22) 得到F(qtemp).
③ 如果F(qtemp) > 0,q1=qtemp,否则qu=qtemp.
④ 重复②、③,直到|F(qtemp)| < 10-4.
3 复杂度分析最优的子载波分配是在N个子载波、K个用户遍历组合,共有KN种可能性分配.因此子载波分配复杂度为O(KN).同时在每一种分配组合中,都需要进行最优功率分配;而提出的能效次优方法只需要一次功率分配,即注水算法(WF, water filling).给定子载波分配下最优的功率分配的复杂度为O(IBPA1+KIWF+IβIBPA2),其中算法第1步需要寻找βmax,涉及二分法BPA1搜索和K个用户的功率注水计算,假设注水算法的复杂度为O(KIWF),二分搜索算法的复杂度为O(IBPA1).而式(22) 的求解需要一维搜索0到βmax及二分搜索算法BPA2,复杂度为O(IβIBPA2).次优的子载波分配的复杂度由2部分组成,能效功率估计和等功率子载波分配,其中等功率子载波分配的计算复杂度为O(KN(lbN)).能效功率估计可以视为3层二分法搜索,分别求得最优的q*、μtemp*及Nk,假设复杂度为O(Ifind_qIfind_μIfind_Nk).
4 仿真结果仿真中设定系统带宽1MHz,分成64个子载波,假设在所有子载波上经历独立同分布的瑞利衰落.系统中有4个用户,基站4根天线,用户2根天线.基站最大发射功率为1W,电路功率消耗为0.2W,功率放大因子0.38.仿真中以文献[6]中的次优最大化频谱效率为对比算法,采用蒙特卡洛仿真,仿真结果为200次独立仿真取均值.
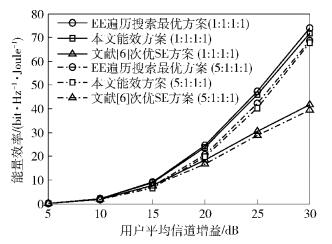
图 1比较了不同方案的能效与谱效性能,可以看出在高信道增益下,提出的能效次优算法比次优谱效算法的能效性能有明显提升;在低信道增益下,能效性能基本相同;所提算法逼近了最优的遍历搜索算法.这是因为在信道增益比较低时,基于能效的发射功率基本是满功率发射,此时与最大化频谱效率问题一样.而在高信道增益下,为了提高系统的能效,所提算法的发射功率小于最大发射功率.图 2给出了不同平均信道增益下吞吐量的性能.从图 2中可以看出,对比算法的频谱效率要优于所提算法.同时,图 1和图 2对比了用户公平性与能效、频谱效率的关系.从图 1和图 2中可以看出,在相同信道条件下,当用户比例速率限制为5:1:1:1时,无论能效还是频谱效率都要低于1:1:1:1时的情况.这是由于系统为保证用户1的速率要求,将许多资源分给用户1导致了系统吞吐量的下降.
|
图 1 能效随用户平均信道增益变化曲线,所有用户的信道条件相同 |

|
图 2 频谱效率随用户平均信道增益变化曲线,所有用户的信道条件相同 |
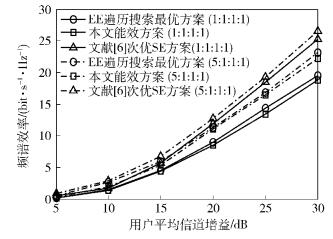
图 3和图 4进一步说明了用户公平性和能效、频谱效率的关系.假设用户1的平均信道增益比其他用户高5dB.比例速率限制分别设定为5:1:1:1和1:1:1:1,从图 3和图 4中可以看出,当比例速率限制为5:1:1:1,系统的能效和频谱效率性能都要高于1:1:1:1.

|
图 3 能效随用户1平均信道增益变化曲线,用户1平均信道增益比其他用户高5dB |
|
图 4 频谱效率随用户1平均信道增益变化曲线,用户1平均信道增益比其他用户高5dB |
图 5给出了在用户1的平均信道增益为25dB时,各用户的归一化速率,可以看出,由于用户1的信道条件优于其他用户,采用容量最大化的贪婪资源分配方式使得用户1获得了大量资源,目的是使系统容量最大,而其他用户则很难保证公平服务.提出的能效方案则可以在满足用户QoS下,公平地分配资源.

|
图 5 各用户归一化速率,用户1平均信道增益为25 dB且比其他用户高5dB |
在多用户MIMO-OFDM系统中,综合考虑用户比例速率限制及总发射功率受限提出了分步优化的资源分配算法.第1步假设子载波共享及平坦衰落,得到能效功率估计,并基于估计功率完成子载波分配.第2步得到了能效最优的功率分配.仿真结果表明,相对次优的频谱效率最大化准则,所提算法在用户高信道增益下保证用户比例公平性的同时可使系统能效获得较大提升.
| [1] | Li Ye, Xu Zhikun, Xiong Cong, et al. Energy-efficient wireless communications: tutorial, survey, and open issues[J].IEEE Wireless Communication Magazine, 2011, 18(6): 28–35. doi: 10.1109/MWC.2011.6108331 |
| [2] | Shen Zukang, Andrews J G, Evans B L. Adaptive resource allocation in multiuser OFDM systems with proportional rate constraints[J].IEEE Transaction on Wireless Communications, 2005, 4(6): 2726–2737. doi: 10.1109/TWC.2005.858010 |
| [3] | Yu Wei, Lan Tian. Transmitter optimization for the multi-antenna downlink with pre-antenna power constraints[J].IEEE Transaction on Signal Processing, 2007, 55(6): 2646–2660. doi: 10.1109/TSP.2006.890905 |
| [4] | Ren Zhanyang, Chen Shanzhi, Hu Bo, et al. Energy-efficient resource allocation in downlink OFDM wireless systems with proportional rate constraints[J].IEEE Transaction on Vehicular Technology, 2014, 63(5): 2139–2150. doi: 10.1109/TVT.2014.2311235 |
| [5] |
赵龙, 龙航, 赵慧, 等. 下行MIMO系统能效最优的功率分配[J]. 北京邮电大学学报, 2013, 36(4): 39–43.
Zhao Long, Long Hang, Zhao Hui, et al. Optimal energy efficient power allocation for downlink MIMO system[J].Journal of Beijing University of Posts and Telecommunications, 2013, 36(4): 39–43. |
| [6] | Xu Jian, Kim J Y, Park W K, et al. Adaptive resource allocation algorithm with fairness for MIMO-OFDMA system[C]//VTC2006 -Spring. Melbourne: IEEE Press, 2006: 1-5. |
| [7] | Ge Xiaohu, Huang Xi, Wang Yuming, et al. Energy-efficiency optimization for MIMO-OFDM mobile multimedia communication systems with QoS constraints[J].IEEE Transaction on Vehicular Technology, 2014, 63(5): 2127–2138. doi: 10.1109/TVT.2014.2310773 |
| [8] | Tse D, Prramod V. Fundamentals of wireless communication[M]. London: Cambridge University Press, 2005. |
| [9] | Xiong Cong, Li Ye, Zhang Shugong, et al. Energy-efficient resource allocation in OFDMA networks[J].IEEE Transaction on Communication, 2012, 60(12): 3874–3886. |
| [10] | Boyd S, Vandeberghe L. Convex optimization[M]. London: Cambridge University Press, 2004. |
| [11] | Isheden C, Chong Z, Jorswieck E, et al. Framework for link-level energy efficiency optimization with informed transmitter[J].IEEE Transaction on Wireless Communications, 2011, 11(8): 2946–2957. |
| [12] | Wang Lichun, Yeh C J. Adaptive joint subchannel and power allocation for multi-user MIMO-OFDM systems[C]//PIMRC '2008. Cannes: IEEE Press, 2008: 1-5. |


