C工程中的非四则运算在所有数值运算中出现的比例为23%.在使用搜索技术进行测试用例生成时, 非四则运算的求解效率很低, 因为非四则运算没有对应的区间运算法则以提高搜索效率.为此, 提出一种等价变换方法, 将非四则运算分解为多个四则运算, 再应用四则运算的区间运算来提高整体的求解效率.实验表明, 此方法能提高非四则运算的测试用例生成效率.
Non-elementary arithmetics accounts for 23% in all numerical calculations in C projects. To solve non-elementary arithmetics is inefficient in fact when search technology is used for test input generation. Because the non-elementary arithmetics does not have corresponding interval arithmetic rules to improve the search efficiency. A method of equivalent transformation was proposed to decompose non-elementary arithmetics into elementary arithmetics. The interval arithmetic of elementary arithmetics can be used thereafter. Experiments show that the test cases of non-elementary arithmetics can be effectively generated by the proposed method.
C语言中的数值运算有11个,分为2类:四则运算为+,-,*,/;非四则运算为%,< < ,>>,& ,|,^,~.对16个开源C工程近15万行代码进行统计,7个非四则运算在数值运算中的比例为23%,在工程中出现的比例为5%.
在使用搜索技术进行测试用例生成时,非四则运算的求解效率很低,因为非四则运算没有对应的区间运算法则. Moore[1]提出区间代数,将1个不确定的值表示成1个区间,并代替具体值进行计算,以得到保守的计算结果. Cousot[2]将区间代数和抽象解释结合起来,可削减约束中变量的区间.王雅文等[3]进一步提出区间集的概念,以更准确地描述变量的取值范围.高洪博等[4]也将区间集的方法应用于二进制代码变量区间分析.
但迄今为止,只有四则运算有对应的区间运算法则.如x和y的初始区间为Dx=[0, 100]和Dy=[0, 100],求满足约束C={x+y=50, x%10=0}的x.对于四则运算x+y=50,可使用区间运算规则(见定义1~2) 计算D′x=[0, 50];但对非四则运算x%10=0,则没有对应的规则计算Dx.
由于非四则运算可分解为四则运算的复合,故提出等价变换方法,将非四则运算转化为多个四则运算,从而应用四则运算的区间运算提高求解效率.进一步,基于搜索框架给出等价变换算法.实验表明,该方法能有效提高测试用例生成效率.
1 相关概念定义1 区间运算:将1个不确定的值表示成1个区间,再用区间代替具体值进行运算,从而得到保守的计算结果.给定任意2个区间[a, b]和[c, d],该方法用到的区间运算规则如下:
1)[a, b] + [c, d] = [a + c, b + d];
2)[a, b]/[c, d] = [min (a/c, a/d, b/c, b/d), max (a/c, a/d, b/c, b/d)],若0∉[c, d];
3)[a, b]∩[c, d] = [max (a, c), min (b, d)],若[a, b]和[c, d]有交集.
例如,整数10的值可表示为[10, 10],整数x的值在0~100之间可表示为[0, 100],则10+x的区间D(10+x)=D(10)+Dx=[10, 10]+[0, 100]=[10, 110],即10+x的取值范围在10~110之间.
定义2 区间削减:给定包含变量x和y的约束C={f(x, y)R a}(以二元约束为例).其中:f(x, y)为x和y的运算表达式,a为常数,R∈{>,≥,< ,≤,=,≠};D={Dx, Dy},Dx和Dy为x和y的初始区间.对约束C进行区间运算以削减x区间的过程称为区间削减[5-6],记为NarrowInterval(C, D, x),x为区间削减的目标变量.
具体过程分为2步:1) 分离目标变量x,有f(x, y) R 0→x R g(y);2) 计算x的区间D′x=Dx∩DR g(y).由于Dx∩DR g(y)≤Dx,故此计算过程能减小x的区间.
例如,D={Dx=[0, 100], Dy=[50, 100]},给定约束C={x-y > 10},以x为目标变量,则NarrowInterval(C, D, x)的过程如下:1) 分离目标变量x-y > 10→x > 10+y;2) 区间运算Dx=Dx∩D > 10+y=Dx∩[min(D(10+y)), MAX]=Dx∩[min(D10+Dy), MAX]=[0, 100]∩[min([10, 10]+[50, 100]), MAX]= [0, 100]∩[60, MAX]=[60, 100].
其中:MAX为x的数据类型的上界.显然,[60, 100] < [0, 100],成功削减了x的区间.
测试用例生成问题可转化为约束求解问题,进而使用搜索算法进行求解[7-8].
定义3 约束求解问题〈X, D, C〉:X为变量集,D为与变量集对应的值域集,C为变量的约束集;X的1个赋值为约束求解问题的1个解,当且仅当此赋值包含所有变量且满足所有约束.
对约束求解问题〈X, D, C〉,使用搜索算法进行求解主要分3步:
1) 从X中选择1个变量Xi进行处理;
2) 从Xi对应的取值域Di中选择1个值Vi;
3) 将〈Xi, Vi〉代入约束集C,若发生矛盾,则从Di中重新选择Vi;否则,继续选择下一组〈Xi+1, Vi+1〉,直至所有变量都赋值.
由于程序中变量的取值域很大,导致第2) 步存在很大的随机性,故常在搜索前,先对变量进行区间削减.
如前例,假定x为整数,则原始搜索空间大小为|Dx|=101(|Dx|为Dx区间内所有元素的个数).经过区间运算后,D′x=[60, 100],即|D′x|=41,取值域削减了60%.故区间运算能减小取值域,从而提高搜索效率.
2 等价变换2.1 问题描述四则运算有对应的区间运算法则,而非四则运算没有.但很多数值运算都可分解为四则运算的复合,故使用分治法,将非四则运算分解为多个四则运算,再分别对每个子运算进行区间运算,从而提高非四则运算的求解效率.
令R为数值集合D上的四则运算,N为D上的非四则运算,则使用等价变换求解N的过程可描述为
1) 问题分解:N={R1, …, Rk},将满足N的数集划分为k个等价类,每个等价类对应1个四则运算.
2) 求解子问题:依次对子问题Ri(1≤i≤k)使用区间运算进行求解,令Si是Ri的解.
3) 合成原问题的解:原问题N的解S=∪Si(1≤i≤k).
非四则运算的具体变换方法如表 1所示.
|
|
表 1 非四则运算的具体变换方法 |
首先给出搜索框架的算法伪码,然后重点描述等价变换相关的子过程.
procedure CSP(X, D, C)
begin
p←buildProblem(X, D, C)
s←Λ
search(p, s);
return s;
end
procedure search (p, s)
begin
if reject(p, s) then return
if accept(p, s) then return
x ← nextVariable(p, s)
s ← extend(s, x);
v ← nextValue(p, s, x)
while v ≠ Λ do
updateValue(s, x, v)
search(p, s)
v ← nextValue(p, s, x)
end
其中:s为当前解,初始为空,记为Λ;search(p, s)为扩展s以找到p的解;reject(p, s)为对约束进行区间运算,若出现变量的值域为空,则表示s不满足约束,返回true,否则返回false;accept(p, s)为若所有变量都已赋值,则s为解,返回true,否则返回false;nextVariable(p, s)为选择下一个需要赋值的变量;extend(s, x)为扩展s,加入新选择的变量x;nextValue(p, s, x)为选择x的下一个值;updateValue(s, x, v)为更新s中变量x的值为v.
与等价变换相关的过程为buildProblem(X, D, C).
procedure buildProblem (X, D, C)
begin
for i = 1 to n do
c ← Ci
if isN(c) then
c′←decompose(c)
replace(C, c, c′)
return new Problem(X, D, C);
end
其中:isN(c)为若c包含非四则运算,则返回true,否则返回false;decompose(c)为将c分解为仅包含四则运算的约束c′;replace(C, c, c′)为将约束集C中的c替换为c′.
3 应用实例为更好说明等价变换的效果,使用如下示例来说明其执行过程.此为判断是否为闰年的C代码,其中包含非四则运算取模.
0:int isLeapYear(int year){
1: if (year%400 == 0)
2: return 1;
3: else if (year%100 == 0)
4: return 0;
5: else if (year%4 == 0)
6: return 1;
7: else
8: return 0;
9:}
假定为路径0129生成测试用例.
1) 初始化约束求解问题的参数:X={year},D={dyear=[1, 10 000]},C={year%400=0}.
2) 构建约束求解问题:p=buildProblem(X, D, C),对取模进行等价变换.
① 分解为四则运算docompose(c):依据变换方法x%y=z→x=yk+z,可知c′={year=400k}.
② 更新约束replace(C, c, R):C={year=400k}.
3) 初始化解s=Λ.
4) 搜索求解.
① 判断矛盾reject(p, s):对C进行区间运算,则Dk=Dyear/D400=[1, 10 000]/[400, 400]=[1, 25],返回false.
② 判断是否所有变量都赋值accept(p, s):由于year还没有赋值,故返回false.
③ 选择变量nextVariable(p, Λ):x=year.
④ 扩展解extend(Λ, year):s=[year].
⑤ 为变量year选值nextValue(p, [year], year):v=400×5=2000(k值任取,此处k=5).
⑥ 更新year的值updateValue([year], year, 2000):s=[year=2000].
⑦ 由于只有1个变量year,且year已赋值,故求解成功.
5) 返回解s=[year=2000],成功生成测试用例.
4 对比实验下面对3个实验场景,进行变换前后的对比实验.
1) 给定1个非四则运算,变量的取值域大小从10逐步增长到10000:验证搜索空间与变换效果之间的关系.
2) 给定20个混合(四则+非四则)运算,非四则运算从0逐步增长到10个:验证非四则运算比例与变换效果之间的关系.
3) 工程中的实例:验证等价变换对覆盖率的影响.
首先是实验设计,然后是实验结果,最后是数据分析、结论以及局限性.
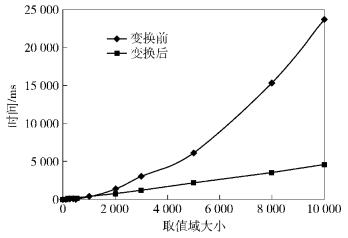
4.1 与搜索空间的关系给定1个非四则运算x R y=a,变量的取值域依次从[1, 10]逐渐增长到[1, 10 000],实验结果如图 1所示.
|
图 1 单个非四则运算变换前后的求解效率对比 |
变换前,2个变量都只能随机取值,故时间复杂度为O(n2);而变换后,只要为1个变量赋值,则另1个变量可通过四则运算求解,即只有1个变量是随机取值,故时间复杂度为O(n).
结论:给定1个非四则运算,搜索空间越大,变换效果越好.
局限性:取值域较小时(小于1000),变换并没有效果.因为在取值域较小时,随机搜索也能很快完成,而等价变换本身会产生额外开销,最终导致等价变换的效果不明显.
4.2 与四则运算比例的关系给定20个运算,包含四则或非四则运算,且非四则运算从0逐渐增长到10个(比例逐渐增大).
1) 变量个数:固定为20个.
2) 变量取值域:都为[1, 5000].
3) 约束形式为x R y rel_op a或x N y rel_op a.其中:R为四则运算,N为非四则运算,rel_op∈{>,≥,< ,≤,=,≠},a为1个[0, 1000]内的随机常数.
4) 变量排序规则:小区间优先+难满足的约束变量优先(Fail Fast规则).
其中:难满足的约束优先级为等式>不等式、四则>非四则.
5) 值排序规则:从小到大.
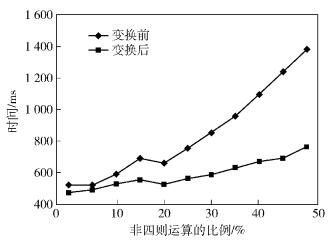
实验结果如图 2所示.
|
图 2 四则+非四则运算变换前后的求解效率对比 |
实验表明,在难满足的约束(如x+y=a)较多时,等价变换效果不明显,因为难满足的约束可通过区间运算将搜索空间S限制为1条线S′(S′«S),在S′基础上再进行等价变换,难以再减小搜索空间,故体现不出变换效果.反之,易满足的约束(如x+y!=c)越多,等价变换效果越好.
结论:非四则运算的比例越大,等价变换的效果越好.
局限性:在难满足的约束(如等式约束)较多时,等价变换的效果不明显.
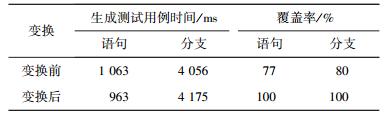
4.3 实际工程测试下面对来自httpd-2.4.6工程(http://httpd.apache.org/download.cgi)的mod_status.c文件的show_time函数进行测试,实验结果如表 2所示.
|
|
表 2 show_time函数变换前后对比 |
由表 2可见,生成测试用例的总时间相差不大,但变换前覆盖率无法达到100%(由于设置搜索回溯次数阈值,在回溯次数达到上限后,会放弃当前覆盖元素,导致覆盖率达不到100%),而变换后的覆盖率达到了100%.
5 结束语针对非四则运算测试用例生成效率低的问题,提出等价变换方法,将非四则运算转化为多个四则运算的复合,从而能应用四则运算的区间运算来提高效率.实验表明,该方法能提高测试用例生成效率,且变量值域越大,非四则运算越多,效果越好.该方法的局限性在于,在等式约束较多时,等价变换效果不明显.主要原因在于,等式约束通过区间运算已大大减小变量取值域,在此基础上再变换,难以进一步减小取值域.
| [1] | Moore R E. Interval analysis[M]. Prentice-Hall, New Jersey, USA, 1966. |
| [2] | Cousot P. Abstract interpretation based formal methods and future challenges[C]//Proceeding Informatics-10 Years Back, 10 Years Ahead, London, 2001: 138-156. |
| [3] |
王雅文, 宫云战, 肖庆, 等. 基于抽象解释的变量值范围分析及应用[J]. 电子学报, 2011, 39(2): 296–303.
Wang Yawen, Gong Yunzhan, Xiao Qing, et al. A method of variable range analysis based on abstract interpretation and its applications[J].Acta Electronica Sinica, 2011, 39(2): 296–303. |
| [4] |
高洪博, 李清宝, 王炜, 等. 基于抽象解释的二进制代码变量区间分析[J]. 电子与信息学报, 2013, 35(8): 1927–1932.
Gao Hongbo, Li Qingbao, Wang Wei, et al. A method of binary code variable interval analysis based on abstract interpretation[J].Journal of Electronics and Information Technology, 2013, 35(8): 1927–1932. |
| [5] |
王志言, 刘椿年. 区间算术在软件测试中的应用[J]. 软件学报, 1998, 9(6): 438–443.
Wang Zhiyan, Liu Chunnian. The application of interval computation in software testing[J].Journal of Software, 1998, 9(6): 438–443. |
| [6] | Wang Yawen, Gong Yunzhan, Chen Junliang, et al. An application of interval analysis in software static analysis[A]. Proceedings of the 2008 IEEE/IFIP International Conference on Embedded and Ubiquito us Computing[C]//NW Washington: IEEE Computer Society, 2008(12): 367-372. |
| [7] | Xing Ying, Gong Yunzhan, Wang Yawen, et al. Path-wise test data generation based on heuristic look-ahead methods[J].Mathematical Problems in Engineering, 2014, 2014: 19. |
| [8] |
邢颖, 宫云战, 王雅文, 等. 基于分支限界搜索框架的测试用例自动生成[J]. 中国科学:信息科学, 2014, 44(10): 1345–1360.
Xing Ying, Gong Yunzhan, Wang Yawen, et al. Branch and bound framework for automatic test case generation[J].Science China: Information Sciences, 2014, 44(10): 1345–1360. |