提出一种基于广义空移键控调制的多输入单输出系统中的物理层安全传输方案.发射端利用合法接收者反馈的信道信息对发送信号进行预处理, 使合法接收者接收的来自各发射天线信号的相位对齐; 同时进行相位旋转来增加星座点间的距离, 从而提高合法接收者的接收性能, 降低误码率.而窃听者接收到的各信号的相位仍然为随机分布, 接收性能明显低于合法接收者.对合法接收者和窃听者的误比特率和保密容量进行了理论和仿真分析.理论和仿真结果表明, 所提方案能明显降低合法接收者的误比特率, 即使在合法信道性能比窃听信道性能要差的情况下, 系统仍然能实现保密传输.
A physical layer security transmission scheme based on generalized space shift keying modulation for multiple-input single-output system was proposed. The transmitter uses the channel state information feedbacked by the legitimate user to preprocess the transmit signals. So the signals received by the legitimate user from each transmit antenna are in phase. Furthermore, the transmitter takes a phase rotation to increase the distances among the constellation points, thereby the performance of the legitimate user is improved and the error rate is reduced. However, the phase of each signal received by the eavesdropper is randomly distributed, so the performance of eavesdropper is significantly inferior to the legitimate user. Analysis and simulation are done for bit error rate of the legitimate user and the eavesdropper. It is shown that the proposed scheme can significantly reduce the legitimate user's bit error rate, even the channel performance of the legitimate user is worse than the eavesdropper, and the secure transmission can be realized.
空间调制[1](SM,spatial modulation)技术是一种使用多天线[2]的传输技术.它可以在系统成本、检测复杂度都较低的前提下,保证系统的数据传输速率与通信质量,减小功率消耗,提高能量效率[3].广义空移键控(GSSK,generalized space shift keying)调制[4]是SM的简化情况,信息只由激活的多根发射天线索引携带. SM技术可应用于物理层安全传输中,增强安全性能. Guan等[5]在SM系统的发射端设计预处理向量,实现系统保密互信息极大化,达到保密通信目的. Sinanovic等[6]只是在常规的空间调制系统中存在窃听者时,对系统的保密容量进行了推导,并未提出具体的物理层安全方案.
在多输入单输出(MISO,multiple inputs single output)系中对利用GSSK调制技术实现信息安全传输的方案进行研究.发送端利用合法信道的信道状态信息对信号进行预处理,使各同时激活的发送天线与合法接收者间的信道的相位对齐,同时进一步进行相位的旋转,使合法接收者空间星座点间的距离极大化,提高其接收性能.对于窃听者,来自各激活天线的接收信号相位仍具有随机性,接收信噪比远低于合法接收者.通过制造合法接收者和窃听者间的接收性能差异,使系统获得保密容量,进而实现信息的安全传输.
1 系统模型系统模型如图 1所示,发送端装备多根天线,发射天线数为Nt,合法接收者和窃听者的接收天线数Nr=1.假设合法接收者能够很好地能获得完美的信道状态信息(CSI,channel state information),并将其无误差地反馈给发送端.假设信道为平坦瑞利衰落信道,合法接收者的信道矢量为H,其元素为hi, i=1, 2, …, Nt,窃听者的信道矢量为G,其元素为gi, i=1, 2, …, Nt. H、G中的元素为服从独立同分布的复高斯随机变量.

|
图 1 GSSK调制物理层安全传输系统模型 |
发送端对信息序列a(n)进行GSSK调制,每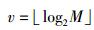


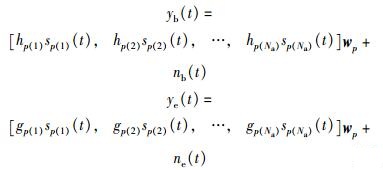
|
(1) |
其中:p(l)∈{1, 2, …, Nt}为第p个空间星座点中第l根天线的索引,l=1, 2, …, Na;hp(l)、gp(l)分别为发射端的第p(l)根发射天线到合法接收者和窃听者的接收天线间的信道增益;sp(l)(t)为第p(l)根天线的发送符号,

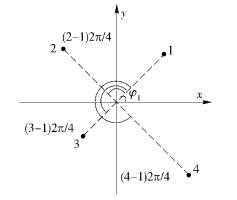
合法接收者选择Nt个无线信道中的一个信道作为参考信道,将其增益中的相位作为参考相位φref.通过反馈链路将各信道与参考信道的相位差值反馈给发送端.设第i个信道链路的相位为φi,i=1, 2, …, Nt.如果参考相位φref=φ1,那么反馈相位差矢量为Φ=[0, φ1-φ2, …, φ1-φNt].发送端的预处理向量wp设计方法如下:令发射端Nt根发射天线所对应信道增益的相位都与参考相位φref对齐.在将各信道的相位对齐后,为增大星座点间距离,还需进行旋转处理.当Nc个星座点经同相位处理后,在任一时隙,假定以星座点1的相位为参考,那么其他星座点相对于星座点1,如空间星座点p,则需有(p-1)(2π/Nc)的相位旋转,通过相位旋转后使星座点间最小欧氏距离极大化,最终星座点幅度决定于激活信道的合并增益,是随机的. Nt=4、Na=2时,星座图如图 2所示.
|
图 2 Nt=4、Na=2时星座点的分布 |
对第p个星座点信号的预处理向量wp为
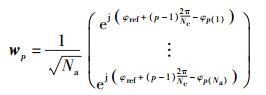
|
(2) |
其中φp(l)是发送端与合法接收者间激活信道的增益系数相位,可看出预处理向量wp是对激活天线对应的发射信号的相位进行处理.
考虑信道加入噪声,那么合法接收者和窃听者的接收信号为

|
(3) |
其中

|
(4) |
其中βp(l)是发送端与窃听者间激活信道增益系数的相位.
3 保密性能分析3.1 误比特率分析合法接收者和窃听者的平均误比特率Pe的联合上界为
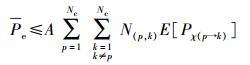
|
(5) |
其中:Pχ(p→k)是空间星座点p与k间的成对差错概率;E[·]表示求期望运算;N(p, k)表示第p个和第k个空间星座点对应比特组的不同比特数目,A=1/[Nclog 2(Nc)];下标χ为b或e,b表示合法接收者,e表示窃听者.对于合法接收者,对接收信号进行最大似然(ML,maximum likelihood)检测的准则为

|
(6) |
其中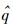

|
(7) |
其中Re{·}表示求实部运算.
假设在特定时隙激活星座点为p,那么i=p时判决统计量为

|
(8) |
其中:|·|表示对星座点的信道增益求模运算,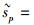
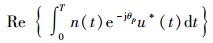
同理可得i≠p时的判决统计量为
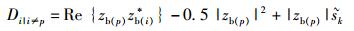
|
(9) |
其中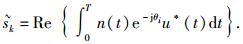
星座点p被错误检测k的成对差错概率为
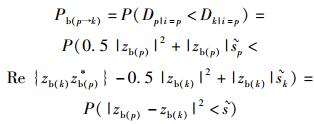
|
(10) |
其中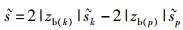

|
(11) |
其中Q(·)表示高斯Q函数.
类似,对窃听者,其成对差错概率为
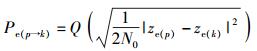
|
(12) |
在得到成对差错概率后,将其带入式(5) 可以得到平均误比特率上界.
下面针对Nt=3、Na=2和Nt=4、Na=2两种情况给出具体的结果.
1) Nt=3、Na=2
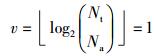
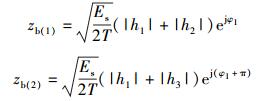
|
(13) |
代入式(11) 中得到合法接收者的成对差错概率为

|
(14) |
其中γ=Es/N0表示信噪比. h1、h2、h3是服从瑞利分布的随机变量,其概率密度函数为f(hj)=hje-hj2/2σj2/σj2,j∈{1, 2, 3},σj2>0.平均成对差错概率为式(14) 对3个信道增益系数求期望
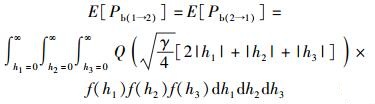
|
(15) |
获得该三重积分的解析式较困难,但可采用数值计算的方式求解.
对于2个星座点的情况而言,由成对差错概率得到的是准确的误比特率.将式(15) 代入式(5) 中,其中A=1/2,N(1, 2)=N(2, 1)=1,得平均误比特率Pe1_b为

|
(16) |
同理对于窃听者差错概率为

|
(17) |
由式(17) 得平均差错概率E[Pe(1→2)]、E[Pe(2→1)],与合法接收者一样,可采用数值计算的方式求解.将E[Pe(1→2)]、E[Pe(2→1)]代入式(5) 得窃听者平均误比特率为
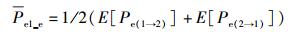
|
(18) |
2) Nt=4、Na=2
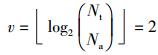
对合法接收者而言,当φ(p, k)=π时,根据式(4)、式(11),有
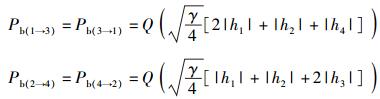
|
(19) |
当φ(p, k)=π/2时,根据式(4)、式(11),有
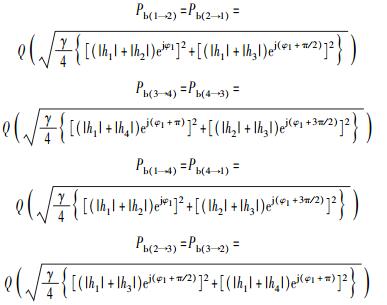
|
(20) |
将式(19)、式(20) 代入式(5) 得平均误比特率上界,其中A=1/8,N(1, 2)=N(2, 1)=N(3, 4)=N(4, 3)=N(1, 3)=N(3, 1)=N(2, 4)=N(4, 2)=1,N(1, 4)=N(4, 1)=N(2, 3)=N(3, 2)=2,故
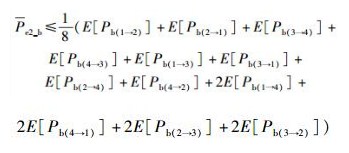
|
(21) |
类似可得到窃听者的平均误比特率上界为
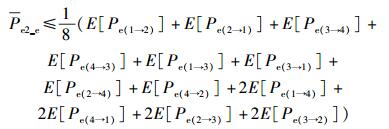
|
(22) |
保密容量是衡量物理层安全技术性能的常用指标.将空间调制的调制器输入端到解调器间的链路看作离散对称信道(DSC,discrete symmetric channel),其信道容量C[7]为
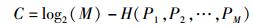
|
(23) |
其中:M为发射端输入符号集个数,P1, P2, …,PM表示接收端信道转移概率,H(·)表示熵函数,表达式为

|
(24) |
对提出方案,发射端输入符号集个数M=Nc,合法接收者和窃听者的信道容量Cb、Ce分别为
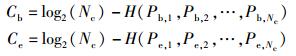
|
(25) |
系统的保密容量Csec 为
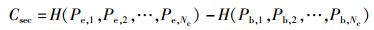
|
(26) |
当Nt=3、Na=2时,星座点数Nc=2,发射端输入符号集个数M=Nc=2,对合法接收端的信道转移概率为Pe1_b、1-Pe1_b,对窃听端的信道转移概率为Pe1_e、1-Pe1_e,其中Pe1_b和Pe1_e为接收端的误符号率,也即上小节合法接收者和窃听者得到的准确平均误比特率,将其代入式(24),再由式(26) 可得到系统的保密容量的准确值.而对于其他Nt、Na可由平均成对错误概率Pb(p→k)、Pe(p→k)得到各转移概率,之后同理可得系统的保密容量.
4 仿真分析下面对采用GSSK调制技术的安全传输系统进行仿真,通过对比合法接收者和窃听者的误比特率和系统的保密容量来衡量系统安全传输性能.仿真中各信道是相互独立的瑞利平坦衰落信道.
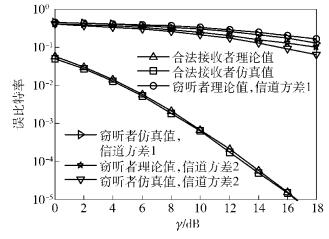
图 3所示为Nt=3、Na=2,各发射天线与合法接收者间的信道方差均为1,而与窃听者的接收天线间的信道方差为1或2时,仿真和理论推导得到的误比特率随信噪比γ的变化曲线.可以看到,理论结果和仿真结果很相近.从合法接收者和窃听者的性能对比来看,当合法接收者的误比特率随信噪比增加而持续下降,而窃听者的误比特率随着信噪比的增加而下降十分缓慢.当窃听者信道的方差为2时,其误码性仍然较高,此时合法接收者信道性能比窃听者的信道性能要差,但合法接收者的误比特率仍然明显低于窃听者.二者间误比特率的显著差距意味着合法接收者能够获得远高于窃听者的信息传输速率,也即能获得可观的保密容量.
|
图 3 Nt=3、Na=2时GSSK调制下合法接收者和窃听者的误比特率 |
图 4所示为Nt=4、Na=2,各发射天线与合法接收者间的信道方差均为1,而与窃听者的接收天线间的信道方差为1或2时,仿真得到的误比特率及其理论上界随信噪比γ的变化曲线.可以看到,仿真结果与理论上界匹配,差距较小,说明理论上界是一个紧界.合法接收者和窃听者的性能对比来看,合法接收者误比特率可随信噪比增加而迅速降低,而窃听者的误比特率则接近0.5.在窃听者信道方差为2时,其误比特率仍然较高,因此即使在合法信道性能比窃听信道性能要差的情况下,系统仍能获得较大保密容量.

|
图 4 Nt=4、Na=2时GSSK调制下合法接收者和窃听者的误比特率 |
图 5给出提出方案与文献[5]方案在系统传输速率为2 bit/符号时,也即提出方案Nt=4、Na=2,文献[5]中Nt=2、幅相调制采用二进制相移键控(BPSK,binary phase shift keying)调制时的误比特率的仿真对比. 2种方案中发射天线与窃听者的接收天线间的信道方差均为1.从仿真图可以看到,提出方案中合法接收者的误比特率要明显低于文献[5]中的合法接收者,而2种方案窃听者的误比特率则接近.因此,随着信噪比的提高,所提出方案的保密容量将明显高于文献[5]的方案.

|
图 5 与文献[5]的误比特率的对比 |
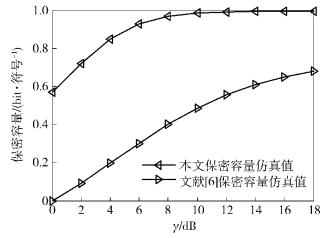
图 6给出了提出方案与文献[6]方案的保密容量的对比.仿真中,Nt=3、Na=2,窃听者的信噪固定为0,而合法接收者的信噪比从0变化到18 dB.从仿真结果可以看到,提出方案的保密容量明显优于未针对安全传输进行设计的文献[6]的方案.
|
图 6 与文献[6]方案中系统的保密容量的对比 |
给出了在MISO系统中的利用GSSK调制技术的物理层安全传输方案.系统通过将信息映射到发射天线索引,利用信道差异来传递信息.发送端对发送信号进行预处理,同时还对信号的星座点进行相位旋转,理论分析和仿真表明所提方案系统具有很强的保密传输能力.
| [1] | Renzo M D, Haas H, Sinanovic S, et al. Spatial modulation[J].IEEE Transactions on Vehicular Technology, 2008, 57(4): 2228–2241. doi: 10.1109/TVT.2007.912136 |
| [2] |
韩东升, 杨维, 许昌龙. Nakagami-m信道下有限反馈多天线系统性能分析[J]. 北京邮电大学学报, 2012, 35(2): 10–14.
Han Dongsheng, Yang Wei, Xu Changlong. Performance analysis of limited feedback multiple antenna systems under Nakagami-m channel[J].Journal of Beijing University of Posts and Telecommunications, 2012, 35(2): 10–14. |
| [3] | Stavridis A, Sinanovic S, Renzo M D, et al. An energy saving base station employing spatial modulation[C]//IEEE 17th International Workshop on Computer Aided Modeling and Design of Communication Links and Networks (CAMAD). Barcelona: IEEE Conference Publications, 2012: 231-235. |
| [4] | Wu C H, Chung W H, Liang H W. Improved generalized space-shift keying via power allocation[J].IEEE Communications Letters, 2014, 18(7): 1143–1146. doi: 10.1109/LCOMM.2014.2326670 |
| [5] | Guan Xinrong, Cai Yueming, Yang Weiwei. On the secrecy mutual information of spatial modulation with finite alphabet[C]//IEEE Wireless Communications Signal Processing (WCSP). Huangshan, China: IEEE Conference Publications, 2012: 1-4. |
| [6] | Sinanovic S, Sreafimovski N, Renzo M D, et al. Secrecy capacity of space keying with two antennas[C]//IEEE Vehicular Technology Conference. Quebec: IEEE Conference Publications, 2012: 1-5. |
| [7] | Maurer U M. Secret key agreement by public discussion from common information[J].IEEE Transactions Information Theory, 1993, 39(3): 733–742. doi: 10.1109/18.256484 |


