2. 长春工业大学 计算机科学与工程学院, 长春 130012
在基于能量检测的脉冲超宽带测距算法中, 如何提高测距精度始终是研究热点.提出一种基于门限比较的两步积分到达时间(TOA)估计算法及相应的门限设置算法.考虑到长积分周期门限比较(TC)算法的测距精度低于短周期, 在前者基础上重新进行短周期积分检测, 构成两步积分TOA估计算法; 根据最优归一化门限与能量采样序列最大值均值比(AMMR)的函数关系, 提出基于AMMR值的门限设置算法(AMMR-TC), 实现了最优归一化门限值的设置.由于短积分周期下, AMMR-TC的性能稍弱于基于能量序列最大最小值比的(MMR-TC)算法, 提出将AMMR-TC与均值-门限比较(MEAN-TC)相结合的AMMR-MEAN-TC算法.仿真分析结果表明测距精度均有一定提高.
2. Institute of Computer Science and Engineering, Changchun University of Technology, Changchun 130012, China
The impulse radio-ultra wideband (IR-UWB) ranging algorithm based on energy detection is widely applied, improving ranging accuracy turns out to be a key point that draws many researchers' attentions. A new two-step-integral time of arrival (TOA) estimation algorithm based on threshold comparison (TC) was proposed, and the corresponding threshold-setting algorithm was also put forward. The ranging accuracy of the TC algorithm for long integration period is lower than that, for short, the two-step-integral TOA estimation algorithm is built up by one more short integration period detection based on long integration period; according to the functional relation between the optimal normalized threshold and advanced maximum energy sample to mean ratio-TC (AMMR-TC) is proposed and the optimal normalized threshold is set. Due to the performance of AMMR-TC is worse than maximum to minimum energy sample ratio-TC (MMR-TC) a little in short integration period, a novel AMMR-MEAN-TC algorithm is put forward in the paper by combining the two algorithms above. Simulations indicate that the ranging accuracy had been improved.
位置感知技术在物联网应用中是极其重要的,是未来物联网产业化的基础.脉冲超宽带(IR-UWB, impulse radio ultra wideband)利用ns级窄脉冲来传输信息,具有良好的时间分辨能力和较高的多径分辨能力,并能达到GHz带宽提供近距离大容量通信,非常适合应用于高精度测距定位[1].基于能量检测的到达时间(TOA, time of arrival)估计算法的主要任务是检测出能量采样序列直达单径分量(DP, direct path)所在的能量块. Guvenc[2-5]等所提出的TOA估计算法,具有一定的指导意义,但是算法的测距精度并不理想,分辨率较低。此外,还有很多关于TOA估计算法的研究[6-7].在已有算法的基础上提出一种基于门限比较(TC, threshold comparison)的两步积分TOA估计算法及相应的门限设置算法,并对所提算法分别进行了仿真分析,结果显示测距精度均有一定提高.
1 系统模型接收的IR-UWB多径信号可表示为
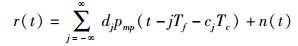
|
(1) |
其中:随机极性码dj∈{±1}用于增加检测信号的处理增益和平滑功率谱密度,pmp(t)表示单个脉冲到达接收端后的信号,j和Tf分别为帧序号和帧周期,Tc为码片周期,一帧内的码片占位数为Nc=Tf/Tc,cj为不同节点分配的跳时序列,cj∈{0, 1, …, Nc-1},n(t)表示加性高斯白噪声.这里仅讨论测距,系统中未考虑调制. pmp(t)可表示为
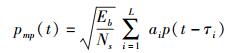
|
(2) |
其中:Eb和Ns分别为符号能量及传送一个符号所使用的脉冲数;p(t)为单位能量的单径脉冲波形,持续时间为Tp;ai和τi分别为各单径的增益和到达时间,其中τ1即为需要估计出的信号到达时间τTOA.为了讨论方便且不失一般性,设dj=1∀j,且接收信号已经预先取得了帧级别的同步[8],即τTOA < Tf,帧间干扰可完全避免[9],即满足Tf>TCIR+CmaxTc,其中TCIR为信道冲激响应的有效持续时间,Cmax为跳时码序列的最大值.通过检测DP所在能量块的精确位置,完成能量检测过程.
2 基于门限比较的两步积分TOA估计算法长积分周期条件下,时间分辨率低,DP位置的估计误差将变大;短积分周期条件下,需要的积分能量块较多,相应的门限比较次数以及存储空间也会随之增加.基于上述2种情况,提出一种基于门限比较的两步积分TOA估计算法(MMR-TC-TC, maximum to mean energy sample ratio -threshold comparison-threshold comparison).
2.1 算法基本思想此算法的基本思想是先采用积分周期时间长的MMR-TC算法[5],找到DP所在的能量块,然后对此DP能量块附近的3个能量块区域进行短周期能量积分,再进行门限比较,进一步搜索DP所在位置.
2.2 仿真分析仿真基于以下条件:IEEE 802.15.4a的CM1和CM2信道下,采用高斯二阶脉冲作为测距脉冲,脉冲宽度为1 ns,脉冲形成因子为0.45 ns;发送端发送1 bit信息,每比特信息占用的脉冲数Ns设置为1;帧周期Tf设置为200 ns;系统采样率为40 GHz;能量采样周期Tb分别设置为1 ns和4 ns;每一次信道实现都设置一个随机均匀分布于(0,Tf)的真实TOA值.仿真迭代次数均为1 000.门限设置为sum(12个能量块)/11.
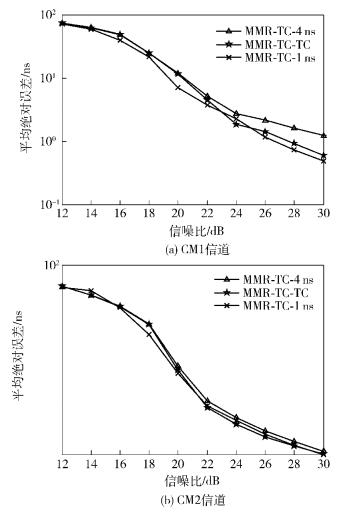
通过图 1可以看出,与MMR-TC相比,当积分周期为4 ns时,所提出的MMR-TC-TC的性能有了较大的提升;当积分周期为1 ns时,性能与MMR-TC接近,但是MMR-TC-TC所需的存储空间和运算复杂度更低,这非常符合无线传感器网络低功耗的特点.
|
图 1 MMR-TC-TC算法与其他TOA估计算法性能比较 |
在门限比较算法中影响算法优劣性能的关键是归一化门限的设置.提出了一种新的门限设置算法——能量采样序列最大值均值比(AMMR, advanced maximum energy sample to mean ratio)算法.在此算法中对归一化门限做了一个新的定义:
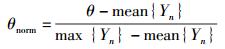
|
(3) |
此算法的基本思想是利用接收信号能量采样序列中的最大值与均值之比,作为参数来对最优归一化门限设置,设r表示AMMR,则其定义可表示为
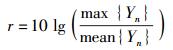
|
(4) |
其中:max{Yn}为接收信号中能量采样序列的最大值,位于信号加噪声区域,mean{Yn}为接收信号能量采样序列的平均值.与MMR相比,相当于把其中的接收信号能量采样序列最小值改为均值,此均值可以把有用信号和噪声均涉及,且在整体上反映了整个信道的信号传输情况,使得最大值与均值之比能更好地反映信噪比和信道特征. 图 2是在IEEE 802.15.4a信道模型的CM1信道和CM2信道下对AMMR与信噪比关系的仿真分析,仿真条件与2.2节相同,图 2是对1 000个独立信道的AMMR值统计平均后的结果,即不同信道的AMMR值可能是不同的,各个信道的AMMR值与具体信道的簇特征和单径分量特征有关.从图 2可以看出,AMMR值随着信噪比的提高而逐步增大,其对应关系比较规律;同一信噪比下不同信道的AMMR值是不同的,即AMMR还能反映一定的信道特征.综上可知,依据AMMR来设置最优归一化门限是合理的.

|
图 2 AMMR的统计平均值随信噪比的变化 |
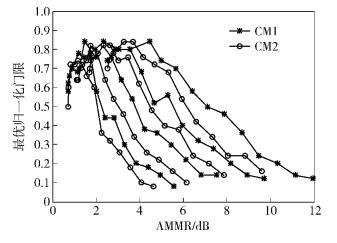
首先,通过大量的仿真实验,寻求AMMR与最优归一化门限的函数关系.参考以前的论文发现积分周期一般取为1 ns、2 ns或4 ns,这里取积分周期分别为1 ns、2 ns、4 ns、8 ns,并在CM1和CM2信道下同时仿真,仿真结果如图 3所示.
|
图 3 最优归一化门限与AMMR之间的关系及其拟合 |
仿真结果显示不同信道下,积分周期不同时,最优归一化门限与AMMR的关系均呈现指数函数关系,图 3同时对两者关系进行指数函数曲线拟合,得到两者的关系函数为
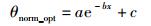
|
(5) |
当最优门限高于0.8时取值为0.8.
AMMR-TC算法的主要流程如下:
1) 计算接收信号能量采样序列Yn;
2) 根据式(4) 计算AMMR值;
3) 根据式(5) 设置最优归一化门限θnorm_opt;
4) 根据式(3) 来计算门限值,其计算表达式为
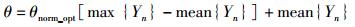
|
(6) |
5) 估计TOA值.
3.3 仿真结果及讨论图 4为IEEE 802.15.4a的CM1和CM2信道下对AMMR-TC算法与MMR-TC算法和3种经典能量检测算法:最大能量选择算法(MES,maximum energy selection)、峰值能量处回溯门限比较算法(MES-SB,maximum energy selection with search back step)和TC算法的仿真对比分析,每个信道下都进行了1 000次独立信道实验.仿真结果显示,在CM1信道下AMMR-TC算法在低中信噪比范围内性能均为最优,在高信噪比范围内与MMR-TC算法最高相差0.3 ns,在CM2信道下AMMR-TC算法基本上在所有信噪比范围内性能都优于MMR-TC算法.
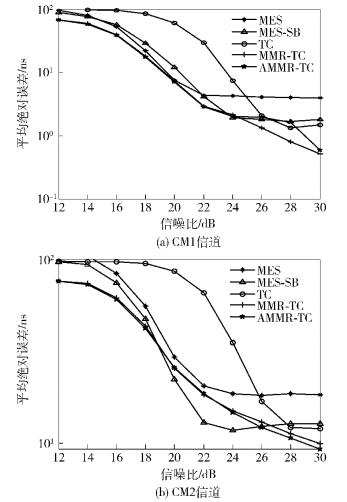
|
图 4 AMMR-TC算法与其他算法的性能对比 (Tb=1 ns) |
针对第3节中AMMR-TC算法在CM1信道下积分周期为1 ns时性能稍弱于MMR-TC算法,笔者提出了一种改进的TOA估计算法——AMMR-MEAN-TC算法.此算法的基本思想是在低中信噪比阶段采用AMMR-TC算法,高信噪比阶段则采用MEAN-TC[7]算法。
图 5所示为CM1信道下Tb取1 ns时x最优值与能量均值的关系曲线,对其进行拟合关系函数为x=2.919×10-6exp(0.203 5y)+1.47,其中y为-10lg(E),当-10lg(E)大于59时,x取2.05;当-10lg(E)位于60到65之间时,出现了奇异点,由于对x值的选取原则为“从0开始累加,找到使误差最小的值”,经过实验验证,此奇异点对仿真结果几乎没有影响.因此,通过此函数求得的x大于2.05时,x均取为2.05即可.
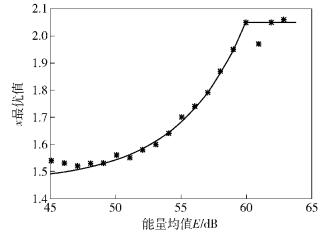
|
图 5 x最优值与能量均值的拟合 |
图 6为AMMR-MEAN-TC算法与其他TOA估计算法的比较.仿真结果显示,AMMR-MEAN-TC算法几乎在所有的信噪比范围内都能获得较小的平均绝对误差,验证了此算法的可行性.
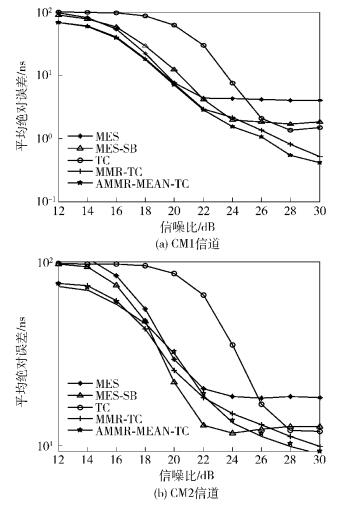
|
图 6 AMMR-MEAN-TC算法与其他TOA算法的比较 |
提出了一种新的TOA估计算法——基于门限比较的两步积分TOA估计算法,在长积分周期条件下检测到能量块后,再次进行短周期计算,同时利用最优归一化门限值,进一步提高了测距精度;由于短积分周期下,AMMR-TC的性能稍弱,提出将AMMR-TC与MEAN-TC 2种算法结合,即AMMR-MEAN-TC算法,进一步改善测距精度.通过大量的仿真实验,在不同信道、不同积分周期条件下,从平均绝对误差、能量均值等方面作了仿真分析,结果显示测距精度均有一定提高.
| [1] | D'Amico A, Mengali U, Taponecco L. TOA estimation with the IEEE 802.15.4a standard[J].IEEE Transactions on Wireless Communications, 2010, 9(7): 2238–2247. doi: 10.1109/TWC.2010.07.090465 |
| [2] | Guvenc I, Sahinoglu Z. Threshold-based TOA estimation for impulse radio UWB systems [C]//IEEE International Conference on Ultra-Wideband. Zurich, 2005: 420-425. |
| [3] | Liu Wenyan, Ding Hong, Huang Xiaotao, et al. TOA estimation in IR-UWB ranging with energy detection receiver using received signal characteristics[J].IEEE Communications Letters, 2012, 16(5): 738–741. doi: 10.1109/LCOMM.2012.030912.112445 |
| [4] | Navarro M, Najar M. Frequency domain joint TOA and DOA estimation in IR-UWB[J].IEEE Transactions on Wireless Communications, 2011, 10(10): 3174–3184. |
| [5] |
吴绍华, 张钦宇, 张乃通. 新颖的基于门限比较的脉冲超宽带TOA估计算法[J]. 通信学报, 2008, 29(7): 7–13.
Wu Shaohua, Zhang Qinyu, Zhang Naitong. Novel threshold-based TOA estimation algorithm for IR-UWB systems[J].Journal on Communications, 2008, 29(7): 7–13. |
| [6] | Taponecco L, D'Amico A, Mengali U. Joint TOA and AOA estimation for UWB localization applications[J].IEEE Transactions on Wireless Communications, 2011, 10(7): 2207–2217. doi: 10.1109/TWC.2011.042211.100966 |
| [7] |
丁锐, 钱志鸿, 王雪. 基于TOA和DOA联合估计的UWB定位方法[J]. 电子与信息学报, 2010, 32(2): 318–322.
Ding Rui, Qian Zhihong, Wang Xue. UWB positioning system based on joint TOA and DOA estimation[J].Journal of Electronics and Information Technology, 2010, 32(2): 318–322. |
| [8] | Tian Z, Giannakis G B. A GLRT approach to data-aided timing acquisition in UWB radios-part I: algorithms[J].IEEE Transactions on Wireless Communications, 2005, 4(6): 2956–2967. doi: 10.1109/TWC.2005.858356 |
| [9] |
阙蔚, 张新跃, 张平, 等. 一种降低UWB系统符号间干扰的方法[J]. 北京邮电大学学报, 2005, 28(5): 74–76.
Que Wei, Zhang Xinyue, Zhang Ping, et al. A novel scheme to counteract inter symbol interference of Ultra-Wideband communication system[J].Journal of Beijing University of Posts and Telecommunications, 2005, 28(5): 74–76. |


