提出一种适用于多输入多输出通信系统的简化的固定复杂度球型译码算法.研究了多天线接收信号的概率分布, 根据接收信号满足卡方分布的特性, 提出利用累计分布函数, 结合检测错误上限确定裁剪半径, 并将检测过程中大于该裁剪半径的节点裁剪掉.仿真结果表明, 简化的固定复杂度球型译码算法在高信噪比的情况下, 可以有效降低计算复杂度.
A further simply the calculation complexity of the fixed-complexity sphere decoding (FSD) was proposed for the multiple-input-multiple-output (MIMO) system. By exploiting the channel noise probability distribution, a threshold determined by the upper bound of the symbol error ratio and cumulative distribution function of Chi-squared distribution can be set to cut nodes with larger metrics. Simulation results show that the proposed algorithm drops the complexity efficiently.
多天线技术是十几年来无线通信领域最重要的物理层技术之一[1-2].最大似然算法可达到最低误比特率,但计算复杂度呈指数增长;线性检测算法具有低计算复杂度,性能较差;串行干扰抵消算法考虑利用已经检测的符号信息,性能得到较大改善[3];球型译码系列算法使得高性能低复杂度的检测成为可能,受到极大的关注[4-8],传统的球型译码算法通过深度优先搜索[9-10],计算复杂度虽然较低,但复杂度不确定[11];宽度优先球型译码算法将搜索方式改为宽度优先,适用于实时系统[12-13].其中,针对固定复杂度球型译码算法,笔者提出采用设定一个合适的阈值,以满足该阈值作为进一步搜索的前提,从而降低搜索过程的复杂度.仿真表明,在QPSK和16QAM2种调制方式下,简化的固定复杂度球型译码算法可分别减少大约50%和70%的复杂度.
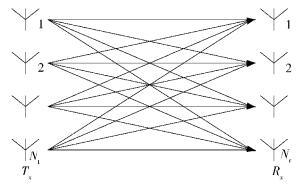
1 多天线系统模型在平衰落信道中,如图 1所示,多天线系统可表示为
|
图 1 多天线系统模型 |
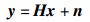
|
(1) |
其中:x为Nt×1维的发送信号矢量,y为Nr×1维的接收信号矢量,为得到唯一的解,通常令Nt≤Nr. n为Nr×1维的独立同分布零均值复加性高斯白噪声,方差为σ2. H为Nr×Nt维信道矩阵,矩阵元素hij为复信道增益,满足E[‖hij2‖]=1.假定Nt=Nr=N/2,但所有结论适用于Nt≤Nr的情况.最大似然检测算法就是计算
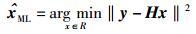
|
(2) |
固定复杂度球型译码算法通过适当减少后期搜索路径的办法,成倍地降低了复杂度.具体过程为
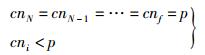
|
(3) |
其中:1≤i < f≤N,p为所有发送符号的可能.
在最开始检测的几层,通常是第N层、第N-1层,展开所有的子节点,后面层展开的子节点数小于可能的符号数.实际上,后面层展开的节点数通常取1,即只展开最好的那个子节点.如图 2所示为固定复杂度球型译码算法的图形表示.其中实线为展开访问的节点,虚线为未展开的节点.

|
图 2 固定复杂度球型译码搜索示意图 |
固定复杂度球型译码算法虽具有相对较低的复杂度,但降低复杂度仍是努力的方向.如何设置一个合适的阈值,在搜索过程中将距离大于该阈值的节点删除,从而有效降低复杂度,这个阈值很关键,既不能过分地降低误码率,又可以有效地删除节点.下面从概率分布的角度来推导合理的阈值取值.
首先研究噪声特性.
噪声功率的分布为卡方分布,其累计分布函数为
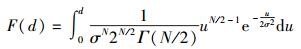
|
(4) |
通过信道的发送矢量与接收矢量的欧式距离可知,F(d)的概率落在以d为半径的圆内.如果设定阈值为d,欧式距离大于d的可能节点都被删除,则因裁剪所引起的错误概率等于1-F(d).
式(4) 也表明,假定正确的累计概率F(d)已知,通过求导运算,则可确定裁剪的阈值d.
反之,从错误概率的角度出发进行逆推运算,错误概率1-F(d),可根据当前情况下的最小误符号率(SER, symbol error ratio),即最大似然误符号率进行约定.在裁剪过程中引发的裁剪错误概率为最小误符号率的1个倍数,即
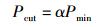
|
(5) |
其中:α为调整因子,用来调整误符号率的损失,通过大量的实验仿真,在计算复杂度和误码性能之间寻求平衡,取α=0.1效果最佳. Pmin为可能的最小误符号率,即当前情况下可调用最大似然误符号率的值. Pcut为因裁剪所引起的误符号率.
所以,最终的错误概率应当为最小误符号率与裁剪误符号率的累加和,即

|
(6) |
则合理的阈值/裁剪半径λ的取值可表示为

|
(7) |
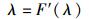
|
(8) |
具体的算法是在每层计算完展开节点后执行,比较这些节点与裁剪半径的大小,若节点大于裁剪半径,则节点被裁剪掉.为保证最后一定有解,即使所有的节点都大于裁剪半径,也要保留1个节点不被裁剪掉.原理如图 3所示.

|
图 3 简化的固定复杂度球型译码搜索示意图 |
根据提出的算法作如下数值仿真实验.仿真实验平台为常见的4发4收多天线系统,假定信道为平衰落的,调制方式分别为QPSK和16QAM方式.
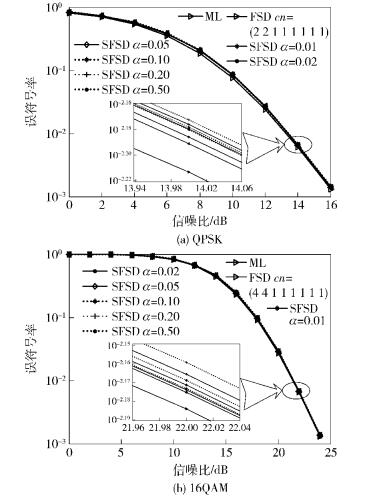
图 4和图 5分别给出了误符号率性能曲线和表示算法复杂度的访问节点数曲线,将最大似然检测(用ML表示)、固定复杂度球型译码检测(用FSD表示)和简化的固定复杂度球型译码检测(用SFSD表示)进行比较.同时,仿真实验也对比了不同调整因子α对性能和复杂度的影响.固定复杂度球型译码检测算法展开节点的取值采用前2层全部展开,其余层只展开1个的做法.
|
图 4 误符号率性能仿真曲线 |

|
图 5 平均访问节点数仿真曲线 |
图 4给出误符号率曲线,横坐标为符号信噪比,单位为dB,纵坐标为误符号率.可以看出,在当前选取的情况下,固定复杂度球型译码算法具有接近最大似然算法的性能.同时,简化的固定复杂度球型译码算法具有接近于固定复杂度球型译码算法和最大似然算法的性能.
图 5给出计算复杂度曲线,复杂度用通用的访问节点数[14]表示.横坐标为信噪比,单位为dB,纵坐标为平均访问节点数.如图 5所示,简化的固定复杂度球型译码算法在低信噪比时,平均访问的节点数减少量较少;在高信噪比时,平均访问的节点数减少量较多;在不同的调整因子α下,减少的量不相同,α越大,复杂度的减少越明显.另外,当信噪比足够高时,简化的固定复杂度球型译码算法在不同的调整因子情况下都趋向相同的访问节点数,该节点数就是串行干扰抵消算法的访问节点数.
4 结束语在多天线系统接收端检测领域,针对高性能算法复杂度高的问题,在固定复杂度球型译码算法的基础上,提出设定一个裁剪半径,裁剪掉距离大于半径的节点,通过研究信道传输的噪声分布特性,并参照最优检测的误符号率上限,可计算出裁剪半径的取值,然后将此取值用于搜索过程中.结果表明,该算法能有效降低原算法的复杂度,尤其是在高信噪比时效果更明显.仿真实验在QPSK调制下信噪比为16时减少了大约50%的访问节点数,在16QAM调制下信噪比为24时减少了大约70%的访问节点数,而性能损失最大不超过0.05 dB.该算法实现简单,在原有固定复杂度球型译码算法的基础上改动很小,非常适合实时系统,具有良好的应用前景.
| [1] | Paulraj A J, Gore D A, Nabar R U. An overview of MIMO communications—a key to gigabit wireless[J].Proceedings of the IEEE, 2004, 92(2): 198–218. doi: 10.1109/JPROC.2003.821915 |
| [2] | Goldsmith A, Jafar S A, Jindal N. Capacity limits of MIMO channels[J].Selected Areas in Communications, IEEE Journal on, 2003, 21(5): 684–702. doi: 10.1109/JSAC.2003.810294 |
| [3] | Golden G D, Foschini C J, Valenzuela R A. Detection algorithm and initial laboratory results using V-BLAST space-time communication architecture[J].Electronics Letters, 1999, 35(1): 14–16. doi: 10.1049/el:19990058 |
| [4] | Vikalo H, Hassibi B. On the sphere-decoding algorithm Ⅱ generalizations, second-order statistics, and applications to communications[J].Signal Processing, IEEE Transactions on, 2005, 53(8): 2819–2834. doi: 10.1109/TSP.2005.850350 |
| [5] | Xu Chong, Gharavi H. A low-complexity solution to decode diversity-oriented block codes in MIMO systems with inter-symbol interference[J].IEEE Transactions on Wireless Communications, 2012, 11(10): 3574–3587. doi: 10.1109/TWC.2012.081612.111819 |
| [6] |
芮国胜, 张海波, 张洋, 等. 接近最优检测性能的低复杂度线性并行MIMO检测算法[J]. 通信学报, 2013, 34(2): 8–14.
Rui Guosheng, Zhang Haibo, Zhang Yang, et al. Low complexity linear parallel detection algorithm for near ML detection of MIMO systems[J].Journal on Communications, 2013, 34(2): 8–14. |
| [7] | Hiraga K, Sakamoto K, Arai M. An SD method utilizing null dependency on transmission distance due to two-ray fading[J].IEEE Antennas and Wireless Propagation Letters, 2014, 13: 126–129. doi: 10.1109/LAWP.2013.2297379 |
| [8] |
彭文杰, 李岳衡, 居美艳, 等. 复合衰落信道下分布式MIMO系统下行中断概率分析[J]. 通信学报, 2014, 35(6): 161–168.
Peng Wenjie, Li Yueheng, Ju Meiyan, et al. Downlink outage probability analysis of distributed MIMO systems over a composite fading channel[J].Journal on Communications, 2014, 35(6): 161–168. |
| [9] | Fincke U, Pohst M. Improved methods for calculating vectors of short length in a lattice, including a complexity analysis[J].Mathematics of Computation, 1985, 44(170): 463–471. doi: 10.1090/S0025-5718-1985-0777278-8 |
| [10] | Schnorr C P, Euchner M. Lattice basis reduction: improved practical algorithms and solving subset sum problems[J].Mathematical Programming, 1994, 66(8): 181–199. |
| [11] | Viterbo E, Boutros J. A universal lattice code decoder for fading channels[J].IEEE Transactions on Information Theory, 1999, 45(5): 1639–1642. doi: 10.1109/18.771234 |
| [12] | Aulin T M. Breadth-first maximum likelihood sequence detection: basics[J].IEEE Transactions on Communications, 1999, 47(2): 208–216. doi: 10.1109/26.752126 |
| [13] | Aulin T M. Breadth-first maximum-likelihood sequence detection: geometry[J].IEEE Transactions on Communications, 2003, 51(12): 2071–2080. doi: 10.1109/TCOMM.2003.813255 |
| [14] | Barbero L G, Thompson J S. Fixing the complexity of the sphere decoder for MIMO detection[J].IEEE Transactions on Wireless Communications, 2008, 7(6): 2131–2142. doi: 10.1109/TWC.2008.060378 |


