2. 西安电子科技大学 计算机学院, 西安 710071
针对深空通信中的低信噪比环境, 提出了一种高动态多普勒频偏捕获的联合检测算法.利用3个码元累积周期来缩小搜索范围, 从而提高多普勒频偏的捕获概率.为了得到捕获概率增量的闭式表达式, 研究了搜索范围对捕获概率的影响.理论分析和仿真结果表明, 在同时存在极低信噪比和高动态多普勒频偏的条件下, 该算法能有效地提高捕获概率和减小捕获误差.
2. School of Computer, Xidian University, Xi'an 710071, China
Under low signal-to-noise ratio in deep-space communications, a joint-detection algorithm was developed for the high dynamic Doppler-shift. This algorithm uses three combination periods to narrow the search range, increasing the acquisition probability for Doppler-shift. To obtain the increase of acquisition probability in a closed-form expression, the impact of search range on acquisition probability was studied. Analysis and its simulation show that this algorithm can efficiently increase the acquisition probability and decrease the acquisition bias under the very low signal-to-noise ratio and high dynamic Doppler-shift.
深空通信[1]中信号收发端之间的远距离传输导致很低的信噪比.另外,高速载体的运动使得载波多普勒频偏呈高动态的变化.为了快速、可靠地捕获到载波多普勒频偏,Wang等[2]提出一种基于期望最大化的自适应估计方法来估计多普勒频偏,但是此方法计算较为复杂.基于快速傅里叶变换(FFT, fast Fourier transform)的多普勒估计方法[3-5]具有速度快、复杂度低等优点, 因此得到了广泛的应用.在低信噪比[5]下,需要采用多个码元信号累积的方式来集中信号能量.但是,高动态多普勒的变化会导致长时间信号累积中的能量扩散现象[4, 6-7].张兆维等[4]定性地分析了搜索范围校正算法,但是并没有定量地给出捕获概率的增加量. Yasotharan等[6]详细指出,信号累积存在一个与多普勒加速度成反比的最佳累积长度. Moo等[7]提出了一种基于运动补偿的算法来抵消多普勒漂移的影响,但是运算复杂度随着加速度的上升而急剧增加.
为了利用相邻码元信号的多普勒频偏漂移受加速度限制的固有特点,笔者提出一种联合检测算法来缩小多普勒频偏的搜索范围,从而提高多普勒频偏的捕获概率.
1 系统模型深空通信接收端天线接收到的信号经载波解调、中频下变频及滤波抽取之后,得到的含有多普勒频偏信息的一个复指数码元信号x=[x0, x1, …, xN-1]为

|
(1) |
其中:a是信号振幅, d∈{-1, +1}是比特速率为rd的码元数据信息,fs是采样频率, fd是码元上的多普勒初始频偏, fa是多普勒频偏加速度, φ0是初始相位,zn是均值为0、方差为σ2的高斯白噪声,N=fs/rd是一个码元信号的长度.
令I=[I0, I1, …, INf-1]=fft(x),其中fft(·)是Nf点复数FFT.根据最大似然检测准则, 多普勒估计值为
在低信噪比情况下,需要长时间累积多个码元信号以提高信号能量.考虑到信号的极性未知(+1或-1),采用非相干累积方式,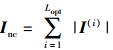
多普勒频偏捕获的联合检测算法需要3个码元信号累积周期,其中每个累积周期内后一个捕获结果的搜索范围是由其他2个累积周期内的捕获结果来共同决定的,如图 1所示.
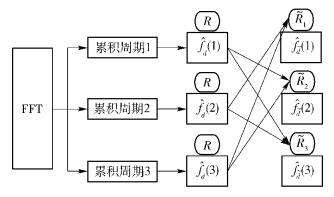
|
图 1 联合检测算法示意图 |
令R=[-Fmax , Fmax ]表示多普勒频偏捕获的初始搜索范围,其中Fmax =fcvmax /c,fc是信号载波频率,vmax是信号收发两端之间的最大相对速度,c=3×108m/s是光速.将接收到的3Lopt个码元信号划分到连续的3个累积周期内并进行非相干累积,然后在搜索范围R内进行3次多普勒估计,得到3个多普勒频偏捕获结果
如果第t(1≤t≤3) 个累积周期内的捕获结果
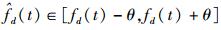
第t个累积周期内的第2次多普勒频偏捕获的搜索范围

|
(2) |
其中:

令p和












定理1 如果fd(1) 满足fd(1)∈

|
(3) |
其中:

证明 令Ln=(2Fmax -2θ)Nf/fs表示处于搜索范围R内的噪声元素个数,那么,元素集合U可以定义为U={u1, …, ui, us, ui+1, …, uLn},其中ui表示第i个噪声,us表示R内最大信号.基于最大似然检测,
假设所有的噪声元素是独立同分布的且累积分布函数是G(λ),那么,可以得到umax 的累积分布函数是[G(λ)]Ln.因此, p=[G(us)]Ln.同样地,搜索范围

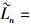


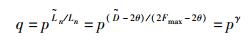
|
(4) |
根据







根据捕获结果
情形1 




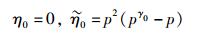
|
(5) |
其中γ0=(
情形2 




|
(6) |
根据定理1,捕获概率的减量和增量分别为

|
(7) |
其中γ1=(
情形3 






|
(8) |
和

|
(9) |
由式(8) 和式(9),可以得到搜索范围

情形3-A fd(1)∈
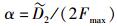
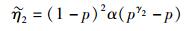
|
(10) |
其中
情形3-B fd(1)∉



|
(11) |
综合以上情形1、情形2和情形3的讨论,可以得到捕获概率的净增量为

|
(12) |
同样的结论可以推广到第2、3个累积周期内获得的捕获结果

接下来,简要分析联合检测算法的计算复杂度.通常,采用蝶形运算的FFT处理需要0.5NflbNf次乘法和NflbNf次加法.另外,非相干累积和谱峰搜索分别需要LoptNf次和Nf次加法.由于深空通信情况下,1 
|
|
表 1 3种算法的复杂度 |
以下通过仿真验证算法的性能,仿真参数:fc=30.0 GHz, vmax =9.0×103 m/s,va=300 m/s2,rd=10.0 kbit/s,fs=40.92 MHz,φ0=0,θ=15.0 kHz,Nf=8 192, 信噪比[-40, -33] dB.
图 2所示为接收信号长度在直接累积算法[5]、最佳累积算法[6]和联合检测算法下的捕获概率曲线.从图 2中可看出,在直接累积算法下,最佳的累积长度Lopt=500.只要接收到的码元个数大于550,联合检测算法就可以提高多普勒捕获概率,如在1 500个码元时,多普勒捕获概率从最佳累积算法的0.80提高到0.89. 图 3所示为联合检测算法性能曲线,从图 3中可以看出,联合检测算法获得的捕获概率在整个信噪比区间上要高于最佳累积算法的捕获概率,如在信噪比-36 dB和-35 dB下,捕获概率分别由0.57和0.80上升到0.71和0.89.

|
图 2 信噪比-35 dB下捕获性能曲线 |

|
图 3 联合检测算法性能曲线 |
为了解决低信噪比下高动态多普勒捕获中信号累积导致的能量扩散问题,提出了一种联合检测算法.该算法利用3个累积周期将多普勒频偏的搜索范围限定到一个更为精确的频率区间,从而提高多普勒捕获概率.仿真结果表明,该算法可以有效地提高深空通信高动态多普勒捕获概率.
| [1] | Marchand N. Digital communications with space applications[J].Proceedings of the IEEE, 1965, 53(9): 1280–1280. |
| [2] | Wang Tianqi, Li Cheng, Meng Weixiao, et al. EM-based adaptive frequency domain estimation of Doppler shifts with CRLB analysis for CDMA systems[J].IEEE Transactions on Communications, 2012, 60(1): 198–298. doi: 10.1109/TCOMM.2011.102011.090300 |
| [3] |
王晓湘, 柯有安. 高动态多普勒频率的最大似然估计器[J]. 北京邮电大学学报, 2000, 23(1): 61–65.
Wang Xiaoxiang, Ke Youan. Maximum likelihood estimation of high dynamic Doppler frequency[J].Journal of Beijing University of Posts and Telecommunicatios, 2000, 23(1): 61–65. |
| [4] |
张兆维, 李文刚, 周彦果, 等. 高动态接收机的多普勒频偏捕获新算法[J]. 西安电子科技大学学报, 2015, 42(2): 7–12.
Zhang Zhaowei, Li Wengang, Zhou Yanguo, et al. New Doppler frequency-shift acquisition algorithm for high dynamic receivers[J].Journal of Xidian University, 2015, 42(2): 7–12. |
| [5] | Borio D, O'Driscoll C, Lachapelle G. Coherent, non-coherent and differentially coherent combining techniques for acquisition of new composite GNSS signals[J].IEEE Transactions on Aerospace and Electronics Systems, 2009, 45(3): 1227–1240. doi: 10.1109/TAES.2009.5259196 |
| [6] | Yasotharan A, Thayaparan T. Strengths and limitations of the Fourier method for detecting accelerating targets by pulse Doppler radar[J].IEEE Proceedings-Radar, Sonar and Navigation, 2002, 49(2): 83–88. |
| [7] | Moo P W, Ding Z. Tracking performance of MIMO radar for accelerating targets[J].IEEE Transactions on Signal Processing, 2013, 61(12): 5205–5216. |



