基于弥聚子论对万有引力定律进行了拓展, 提出了包含引力作用和斥力作用、普适于微观、介观和宏观领域的全宇观万有作用力假说, 建立了全宇观万有作用力公式.其基本依据是:当实物体的弥聚宗量Bm从0变至∞时, 由全宇观量子化变量hB表征的实物体的波动性从最大(hB=h)降至最小(hB=hΔ), 而其粒子性则相应地从最小升至最大.其要点包括:① 当一对实物体的粒子性一起达到其共同的上限时, 万有引力定律对于这对实物体严格地成立; ② 在一般情况下, 一对实物体之间万有作用力的性质(引力或斥力)与它们各自的全宇观量子化变量hB1、hB2以及彼此之间的距离r相关; ③ 存在一个与上述实物体各自的波函数空间延伸线度S1和S2(分别由hB1和hB2决定)相关的临界距离rc, 万有作用力的性质在r=rc时发生逆转:r>rc时表现为引力, r < rc时表现为斥力.此假说的正确性有待实验检验, 但一经证实, 其意义或许是不容忽略的.它有可能在固体物理学相关物理机制的诠释方面起到某种作用, 甚至还有可能为广义相对论的进一步发展提供线索.
Based on the bivergentum theory, the law of universal gravitation is extended to the hypothesis of full-cosmic-scope (FCS) universal interaction force, which involves not only the attractive forces but also the repulsive forces and applies to the microscopic, the meso-scopic and the macroscopic regimes, and the formula of FCS universal interaction force is established. The basic principle is that the wave property of a real physical object with the FCS quantization variable hB as its measure decreases from its maximum (hB=h) to its minimum (hB=hΔ) and correspondingly the particle property of the object increases from its minimum to its maximum when the bivergentum argument Bm of the object varies from 0 to ∞. The main points include ① the law of universal gravitation is rigorously valid for a pair of real physical objects when the particle properties of both objects reach their common upper limit. ② In general cases, the property of the universal interaction force (attractive or repulsive) between a pair of real physical objects is related to their FCS quantization variables hB1, hB2 and the distance r between them. ③ There exists a critical distance rc related to the spatial extension dimensions S1 and S2 of the two objects' wave functions (determined by hB1 and hB2). The reversal of the property of the universal interaction force happens at the point r=rc, i.e. the force manifests itself as an attractive force when r>rc and as a repulsive force when r < rc. The truthfulness of this hypothesis needs to be tested by experiments. However, once it would be proved, the significance of this advancement might not be ignored. Probably, it might be contributive to the interpretations of relevant physical mechanisms in solid state physics, and might even give a clue to the further evolution of the theory of general relativity.
万有引力定律是牛顿的伟大发现,是经典力学中最基本的定律之一,其表达式为[1]
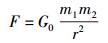
|
(1) |
其中:m1和m2分别为2个相互作用的质点(实物体)各自的引力质量;r为该2质点之间的距离;F为该2质点之间的引力,即万有引力;G0=6.672×10-11m3kg-1s-2为万有引力常数.
万有引力定律在宏观领域中的应用取得了巨大的成功.尽管它无法解释水星近日点的进动,无法破解Neuman-Zeeliger基于无穷大引力场推论的诘难,也无法满足狭义相对论要求的洛仑兹协变性,同时还因其超距作用性质而受到诟病,但它在相当广阔的应用范围内仍然不失为一种高度精确的理论[2].
然而,万有引力定律在微观世界中的应用则鲜有提及,这是因为微观实物粒子(以下简称“微观粒子”)之间按照万有引力定律计算出来的与质量相关的引力要比按照库仑定律计算出来的与电荷量相关的库仑作用力(引力或斥力)小得多,因而万有引力便被理所当然地忽略了.这一看似无可厚非的认识和做法却在事实上“屏蔽”了人们对于万有引力定律在微观世界中适用性的进一步思考.这对于物理学的发展或许是个遗憾.
其实,简单地认定万有引力定律这一从宏观现象中归纳出来的定律在微观领域中仍然适用是缺乏理论和实验依据的.思及分别由经典力学和量子力学所描述的宏观实物体和微观粒子行为特征之间偌大的差异,也许反过来假定万有引力定律在微观领域不再适用或至少是不完全适用才更符合事物发展的一般逻辑.于是,万有引力定律在这样的假定下将会发生怎样的变化,或者将面临怎样的拓展或修正,就成为一个非常重要而有趣的问题.
不过,也许会出现这样的看法:既然依据现有理论微观粒子之间的“万有引力”远小于相应的库仑作用力以至于可以忽略,而实验上也没有发现“万有引力”作用明显地存在于微观物理过程中的迹象,那么针对微观粒子之间相互作用的情形重新审视乃至修订万有引力定律似乎就没有太大的必要了.对此,笔者的见解是,就科学意义而言,无论一个物理量多么微小,对于它的了解和研究都是必要的.譬如,在固体物理学中,范德瓦耳斯力和以离子键、共价键相结合的原子之间的作用力相比就是微乎其微的,但若离开它,具有稳固结构的原子和分子(包括惰性气体元素和共价键饱和分子)也能够结合为晶体的事实就无法解释了[3-5].另外,如所周知,激光器中的自发发射强度较之激光强度而言极其微弱,但正是前者引发了后者.因此,笔者坚信依循上述假定拓展或修正万有引力定律的努力至少和确证万有引力定律在微观领域仍然适用的努力具有同等的意义.
所幸先前提出的弥聚子论[6-14]为探究上述问题开辟了一个新的视角,下文将在简述弥聚子论相关要点之后具体探究这个问题.
1 弥聚子论相关要点简述[8-9, 14]弥聚宗量Bm是弥聚子论中用来表征与宇观程度(宏观或微观程度)直接相关、与粒子性强度或波动性强度一一对应的实物体弥聚程度的物理量.其表达式为
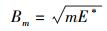
|
(2) |
其中:E*为全宇观波动方程的定态波函数解中能态分布峰值处的能量(以下简称“能量”),m为全宇观狭义相对论质量并被认为等同于引力质量(以下一并简称“质量”).这里需要说明的是,在先前发表的与弥聚子论相关的文献[6-14]中,一直是按照量子力学的表述习惯用字母μ来表示质量的,但在此处为了保持与万有引力定律中质量的表示符号一致,特将其记作m.弥聚宗量Bm的变化范围为(0, ∞).随着Bm从0变至∞,实物体的波动性从最大变至最小,而其粒子性则从最小变至最大;相应地,作为波动性自然强度的表征,全宇观量子化变量
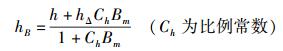
|
(3) |
从最大变至最小,即从h(普朗克常数)变至hΔ.
与此相伴随的变化还包括实物体能级的弥散和实物体波函数的空间聚敛.前者意味着能级具有一定的宽度,后者意味着波函数具有一定的空间延伸线度.下文中将会涉及波函数的空间延伸线度S,其表达式为
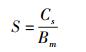
|
(4) |
其中Cs为比例常数.
弥聚子论认为,经典力学是弥聚宗量Bm→∞时的理论,而量子力学则是弥聚宗量Bm→0时的理论.
2 全宇观万有作用力唯象理论万有引力定律涉及2个实物体(可分别称作实物体1和实物体2).设它们的质量分别为m1和m2,能量分别为E1*和E2*,则根据式(2) 和式(3),它们的弥聚宗量分别为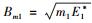
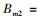
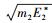

|
(5) |
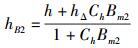
|
(6) |
而相应的波函数延伸线度则分别为

|
(7) |

|
(8) |
为了下文表述方便,兹将S1与S2之和定义为一个新的物理量rc,即
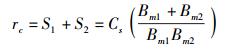
|
(9) |
从式(5) 和式(6) 解得Bm1和Bm2,并将其代入式(9),可以给出rc的另外一种形式:
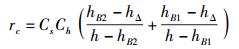
|
(10) |
显然,依据弥聚子论,首先可以确认,万有引力定律必在理想的经典力学情形下,即2个实物体的粒子性都达到极致(Bm1→∞且Bm2→∞,亦即hB1→hΔ且hB2→hΔ)时成立;其次,依据与万有引力定律有关的大量实验事实,该定律应在Bm1和Bm2足够大,亦即hB1和hB2足够小时也相当精确地成立.
然而,当Bm1和Bm2的取值显著变小,亦即hB1和hB2的取值显著变大,以至于2个实物体的粒子性下降至次要地位、波动性上升至主导地位的时候,万有引力定律的适用性或正确性就值得质疑了.因为当实物体的本征属性发生如此显著的变化乃至逆转时,它们之间的相互作用规律却能够完全保持不变是难以想象的,这和牛顿第二定律能够适用于微观领域一样难以想象.因此,假定它们之间的相互作用规律会发生变化至少具有哲学和逻辑上的合理性;再者,由于导致这种变化的因素Bm1、Bm2或hB1和hB2是可以连续演化的,故这种变化也应该是一种连续性的渐变.可见,尝试给出能够反映这种“渐变”过程的、新的有关实物体之间相互作用力的模型和公式是有意义的.
接下来,还必须考虑一个问题,即这种变化可以“剧烈”到什么程度?或者说,这种变化会不会由量变引发质变?笔者的答案是肯定的.鉴于实物体对于空间的占据具有排他性,亦即具有抗拒其他实物体进入其波函数空间延伸线度之内的倾向,同时鉴于固体中具有稳固结构,通常呈现电中性的原子或分子之间也存在着排斥作用[3-5],不妨假定当Bm1和Bm2的取值足够小,亦即hB1和hB2的取值足够大,以至于S1和S2之和rc达到实物体间距r,即
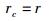
|
(11) |
时,伴随着2个实物体的联合本征属性由粒子性占主导地位向波动性占主导地位的逆转,二者之间的相互作用将发生由引力到斥力的逆转或质变.这种效应也许和范德瓦耳斯作用是共存的或相联系的.
显然,在定量描述上述逆转或质变时,引入因子(r-rc)是必要的.这是因为当式(11) 成立时,r-rc=0,恰好对应于上述逆转或质变的发生.而当r>rc时和r < rc时,该因子分别取正值和负值,可分别表示引力和斥力2种情形.因此,可将rc称作引力和斥力相互转换的临界距离.
以上的假设和构想实际上已经将原来的“万有引力”概念拓展为既包含引力也包含斥力、既适合宏观领域也适合微观及介观领域的“全宇观万有作用力”的新概念.依据这些假设和构想即可将万有引力定律公式唯象地拓展为全宇观万有作用力公式.
首先,假定全宇观万有作用力FB正比于因子(r-rc),同时正比于式(1) 中给出的反映宏观情形的因子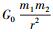

|
(12) |
然后,再引入一个恒正自洽因子f(r, rc),即可令

|
(13) |
其中自洽因子f(r, rc)被一般化地设为r和rc的函数.这是因为,简单尝试表明,该因子不可能为常数,否则在2个实物体的粒子性达到极致的情况下,由于rc→0(根据式(9) 或式(10)),亦即(r-rc)=r(r为变量),式(13) 将无法蜕化为式(1);同时,容易看出,该因子的量纲应与因子(r-rc)的量纲成倒数关系.据此,可设其具有如下形式:
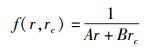
|
(14) |
其中A和B为待定常数.
将式(14) 代入式(13) 即得
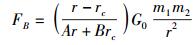
|
(15) |
根据式(9) 或式(10) 可知,当2个实物体的粒子性都达到极致时,应有rc=0.此时,式(15) 应蜕化为式(1),即有
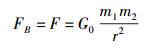
|
(16) |
亦即

|
(17) |
解之立得

|
(18) |
类似地,如前所述,当2个实物体的波动性都达到极致时,rc=∞.此时,式(15) 应蜕化为

|
(19) |
其中:G∞为2个实物体的波动性都达到极致时的万有作用力常数(取正值;且一般而言应不同于G0),右端的负号则表示此时的万有作用力表现为排斥力.
具体地,应有
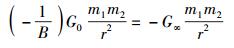
|
(20) |
解之立得
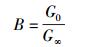
|
(21) |
将式(18) 和式(21) 代入式(15) 可得最终的全宇观万有作用力公式为
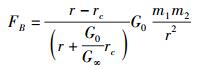
|
(22) |
稍加改写,可得更为对称的形式:
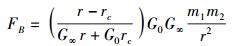
|
(23) |
至此,全宇观万有作用力公式建立完毕.
最后,作一点并非必要的补充:鉴于在同时表述引力和斥力的情况下,约定引力取负值、斥力取正值更符合通常的习惯(文献[2]和文献[15]中即有遵从这一约定的例子),可将式(22) 和式(23) 分别改写为
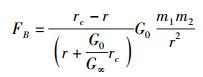
|
(24) |
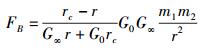
|
(25) |
式(24) 与式(22)、式(25) 与式(23) 的差别仅在于将因子(r-rc)替换为因子(rc-r).这一差别仅仅是形式上的差别,就实质而言,式(24) 与式(22)、式(25) 与式(23) 是完全相同的.
3 结束语上述理论,包括全宇观万有作用力的概念以及采用唯象方法建立的全宇观万有作用力公式,具有较强的逻辑上的合理性和甚为诱人的科学美感,但目前还只是一个假说,其正确性有待实验的检验.不过,一旦该理论被证明是正确的,其意义或许是不容忽略的.它有可能在固体物理学相关物理机制的诠释方面起到某种作用,甚至还有可能为广义相对论的进一步发展提供线索.
致谢: 此工作得益于与刘伟副教授、王俊副教授的交流和讨论,并得到了成卓同学的协助,谨致谢意.| [1] | 程守洙, 江之永. 普通物理学:第一册[M]. 3版. 北京: 人民教育出版社, 1978: 51-52. |
| [2] | 刘辽, 赵铮. 广义相对论[M]. 2版. 北京: 高等教育出版社, 2004: 1-4. |
| [3] | 黄昆. 固体物理学[M]. 韩汝琦, 改编. 北京: 高等教育出版社, 1988: 49-55. |
| [4] | M·A·奥默尔. 固体物理学基础[M]. 贾明, 张文彬, 李振亚, 等译. 王镇皋, 校. 北京: 北京师范大学出版社, 1987: 23-25. |
| [5] | 方俊鑫, 陆栋. 固体物理学:上册[M]. 上海: 上海科学技术出版社, 1980: 71-74. |
| [6] | Ren Xiaomin. Theoretical investigation on the continuous evolution of the electron-gas dimensionality: from bulk materials to quantum dots (postdeadline paper, AF4A. 6)[C]// 2012 Asia Communication and Photonics Conference (ACP). Guangzhou: [s.n.], 2012: 1-4. |
| [7] | Ren Xiaomin. Modification of the theory on the energy-level dispersion and the continuity of the electron-gas dimensionality (invited talk/plenary session) [C]//21st International Symposium on Nanostructures: Physics and Technology (Nano). St. Petersburg: [s.n.], 2013: 347-349. |
| [8] | Ren Xiaomin. Novel understanding of electron states architecture and its dimensionality in semiconductors[J].Optics and Photonics Journal, 2013, 3(28): 322–330. |
| [9] | Ren Xiaomin. Started with the energy-level dispersion: the past one year (Invited talk, Track-1, AF4A. 1) [C]//2013 Asia Communication and Photonics Conference, co-located and jointly organized with 2013 International Conference on Information Photonics and Optical Communications (ACP/IPOC). Beijing: [s.n.], 2013: 1-3. |
| [10] | Ren Xiaomin, Duan Xiaofeng, Liu Xiaolong, et al. On the validity of the newly proposed bivergentum mechanics: one ready-for-long evidence and two intriguing predictions (postdeadline paper, AF2A. 1) [C]//2013 Asia Communication and Photonics Conference, co-located and jointly organized with 2013 International Conference on Information Photonics and Optical Communications (ACP/IPOC). Beijing: [s.n.], 2013: 1-5. |
| [11] | Ren Xiaomin. Fundamental hypotheses: complex and anisotropic mass, full cosmic-scope uncertainty & wave-particle duality, and novel understanding of wave-function collapse (invited talk at the session of Interdisciplinary Sciences) [C]//The 8th Joint Meeting of Chinese Physicists Worldwide (OCPA8, also called as International Conference on Physics & Education-Looking Forward to Quantum Frontiers and Beyond). Singapore: [s.n.], 2014: 57. |
| [12] | Ren Xiaomin. From fractional dimensionality of electron-states architecture to unusual revelations in fundamental physics (invited talk, recorded in the Conference Program Guide)[C]//2014 International Symposium on Photonics and Optoelectronics (SOPO). Suzhou: [s.n.], 2014: 6-7. |
| [13] |
任晓敏. 能级弥散、分数维度电子态系与纳米光电子学(大会特邀报告) [C]//第九届全国光子学学术会议暨中国光学学会纤维光学与集成光学专业委员会成立30周年大会. 成都: [s. n. ], 2014: 10.
Ren Xiaomin. Energy-level dispersion, fractional-dimensionality electron states architecture and nano-opoelectronics (plenary talk, recorded in the conference program guide)[C]//9th National Academic Conference on Photonics as Well as 30th Anniversary Conference of the Specialized Committee of Fibre Optics and Integrated Optics of the Chinese Optical Society. Chengdu: [s. n. ], 2014: 10. |
| [14] | RenXiaomin. Scientific characterization of wave property and particle property of matters and the mutual conversion between photons and symitons[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(1): 1–10. |
| [15] | 徐龙道, 等. 物理学词典[M]. 北京: 科学出版社, 2004: 10-11. |


