数字签名阐明了数字消息或文档的可验证性，只有拥有私钥的用户对其签名，签名可以被公开验证.但数字签名方案在签名的过程中需要大量的复杂的计算，在某些特殊的环境中，特别是计算能力要求较低的轻量设备(移动自组网络和智能卡等)，在短时间内完成复杂的计算是不可能的.在线/离线签名是一种能有效提高签名效率的技术，特别适用于计算能力受限的传感器和移动互联网中的终端设备. Even等^[1]首次提出了在线/离线签名的概念，该方案将数字签名分成两个阶段^[1-7]，即在线签名阶段和离线签名阶段.离线签名阶段，是在未知签名消息的情况下实行签名预计算，此阶段包含签名之前的一些复杂计算；在线签名阶段，输入消息，生成所需要的签名，此阶段签名速度非常快.

但目前大多数的研究是基于传统数论困难问题构造的，如基于因式分解、基于离散对数问题.最近，格公钥因能够抵抗量子计算攻击的特性而受到了广泛的关注.为此利用Bonsai技术，构造了一个新的格上基于身份在线/离线签名方案，在小整数解(SIS，small integer solution)困难问题下，证明了新方案具有抗适应性选择消息攻击的强不可伪造性(sUF-CMA，strongly unforgeable against adaptive chosen message attacks)，从而在提高方案安全性的同时，改进了方案的实现效率.

定义1 设B=(v₁, v₂, …, v_m)∈是m维空间的一组基，则格，这里v₁, …, v_m是一组线性无关的向量.

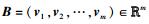
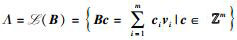
定义2 给定一个整数q，一个矩阵和一个实数β.小整数解问题SIS：找到一个非零向量e，使得Ae=0mod q且‖e‖≤β.

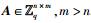
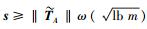
引理1^[8] 设q≥2，矩阵.设T_A是格Λ_q^⊥(A)的一组基，.则有：

1) 对于两个向量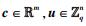，存在一个概率多项式时间(PPT，probabilistic polynomial time)算法SamplePre(A, T_A, u, s)，返回一个向量e∈Λ_q^⊥(A)，使得e的分布统计接近于D_{Λ, s, c}；

2) 如果向量e是D_{Λ, s, c}一个抽样，即有.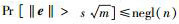

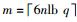
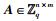
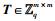
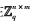
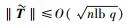
引理2^[8] 设q≥3是一个奇数且.那么存在一个PPT算法TrapGen(q, n, m)，输出矩阵和，其中A在上是接近于均匀的，T是格Λ_q^⊥(A)的一组基，且除了以不可忽略的概率外都满足和‖T‖≤O(nlb q).

引理3^[9] 设n和q是正整数，且q是素数，m≥6nlb q.对于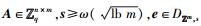，则u的分布统计接近于Λ_q^⊥(A)上的均匀分布且u=Aemod q.

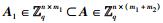
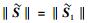
引理4^[10] 输入格Λ_q^⊥(A₁)的一组基S₁，一个矩阵，如果m₁≥6nlb q，存在一个PPT算法ExtBasis(S₁, A=A₁|A₂)输出格Λ_q^⊥(A)的一组基S且.

Gentry等^[8]使用Bonsai技术构造了一个签名方案，具体算法由以下3个部分组成.

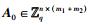
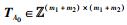
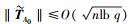
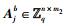
1) 秘钥生成:运行陷门生成算法TrapGen(q, n, m)生成一个矩阵和Λ_q^⊥(A₀)上的一个短基(这里m=m₁+(k+1)m₂)，使得，对于每个(b, j)∈{0, 1}×[k]，生成一个均匀独立的矩阵，输vk=(A₀, {A_j^b})和sk=T_A0.

2) 签名:令A_μ=[A₀|A₁^μ₁|…|A_k^μ_k]，通过密钥扩展算法计算T_μ=ExtBasis(T_A0, A_μ)，输出签名e=SamplePre(T_μ, s, u).

3) 验证:令A_μ=[A₀|A₁^μ₁|…|A_k^μ_k]，验证e≠0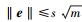，和A_μe=u mod q是否成立，若以上条件同时成立，则签名有效，输出1；否则，输出0.

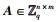
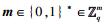
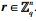
定义3 给定一个素数q，1个矩阵，2个向量和.存在1个变色龙哈希函数H₁，满足H₁(m, r)=Am+r.

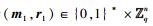
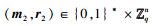
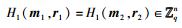
引理5^[11-12] 对于和，存在1个H₁算法，使得且m₁≠m₂.

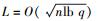
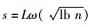
定义参数分别为m=O(nlb q)，和高斯参数，该方案由以下5个算法组成.

参数建立:输入1个安全参数n，设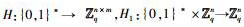是2个安全的哈希函数，算法执行如下.

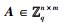
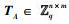
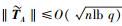
1) 运行陷门生成算法TrapGen(q, n, m)生成1个矩阵和Λ_q^⊥(A)上的1个短基，使得.

2) 对于任意用户的身份I∈{0, 1}^*，随机选取1个矩阵，这里.

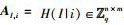
3) 输出系统公开参数(A, A_I, H, H₁)，保存主密钥T_A.

密钥提取:输入系统公开参数，用户的身份I，算法执行如下.

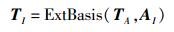
输出用户的私钥T_I.

离线签名:输入系统公开参数，1个随机的向量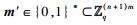，用户执行如下算法.

1) 选取一个随机数.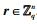

2) 计算u=H₁(m′, r).

3) 计算e=SamplePre(A_I, T_I, s, u).

4) 输出离线签名σ^off=e，保存(u, r).

在线签名:输入系统公开参数，消息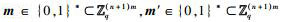和离线签名σ^off，用户执行如下算法.

1) 计算k=A_I(m′－m)+r.

2) 消息m的在线签名σ^on=k.

3) 输出签名σ=(σ^on, σ^off)=(e, k).

验证:输入用户的身份I，消息m和签名σ，验证者首先计算u=H₁(m, k)(由引理4可知)，并验证如下算法.

1) .

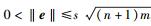
2) A_Ie=u.

若以上条件同时成立，则签名有效，输出1；否则，输出0.

定理1 在随机预言模型下，如果存在1个概率多项式时间的敌手A在时间t内经过q_H次H询问，q_H1次H₁询问，q_E次密钥提取询问，q_S次签名询问之后以优势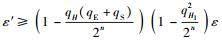抗适应性选择消息攻击的强不可伪造性(sUF-CMA, strongly un-forgeability under chosen message attack)，那么存在一个算法B能解SIS问题实例.这里运行的时间为t′=t+q_Ht_H+(q_H1+q_S)t_H1+q_St_ExtBasis+q_St_SamplePre，这里q_(·)和t_(·)分别表示执行询问的次数和执行询问的时间.

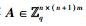
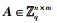
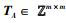
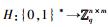
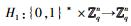
证明 假设存在一个多项式时间的敌手A，构造一个不可区分的算法B用敌手A解SIS问题，即输入任意一个矩阵，找到一个非零向量z≠0，使得Az=0 mod q.在生成参数之前，敌手A提供一个挑战的身份I^*.这时B运行算法TrapGen(q, n, m)生成一个公钥和一个私钥T_A∈. B随机选取两个哈希函数，，计算A_I=A|A_{I, 1}|…|A_{I, n}，其中A_{I, i}=H(I|i).最后，将(A_I, H, H₁)发给A.不失一般性，假设所有的哈希函数值都是由B生成的.下面B回答4个随机预言机询问：H询问、H₁询问、密钥提取询问和签名询问，且B维护3张列表L，L₁和L₂.具体过程如下.

H询问: B维护一张H询问的列表L，列表初始值为空.假设I是新鲜的，并之前没有被询问过.那么A对随机预言机H进行询问，B执行如下.

1) 若I=I^*，即在列表L中存在匹配的哈希值，B直接返回对应的值.

2) 若I≠I^*，B随机选取1个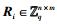，将R_i作为对H询问的响应，并将(I|i, R_i)添加到列表L中.

H₁询问: B维护一张H₁询问的列表L₁，列表初始值为空. A对随机预言机H₁进行询问，如果列表L₁中存在匹配的哈希值，B直接返回对应的值.否则B随机选取1个u，将u作为对H₁询问的响应，并将(A_I, m′, r, u)添加到列表L₁中.

密钥提取询问:为了响应A对用户身份I的密钥提取询问，B执行如下.

1) 若I=I^*，B退出.

2) 若I≠I^*，B从列表L中找到(I|i, R_i)，计算A_I=A|A_{I, 1}|…|A_{I, n}和T_I=ExtBasis(T_A, A_I)，T_I为对应用户身份I的私钥.最后，B将(A_I, I|i, T_I)存储到L₂中.

签名询问:为了响应A对消息m和身份I签名的询问，B模拟出有效的签名. B从列表L，L₁和L₂中分别找到(I|i, R_i)，(A_I, m′, r, u)和(A_I, I|i, T_I).那么对于任意的i∈(1, 2, …, n)，此时的签名询问分为2个阶段，即离线签名询问和在线签名询问. B执行如下.

1) 离线签名询问：B选取1个随机数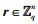，计算u=H₁(m′, r)，e=SamplePre(A_I, T_I, s, u)，输出离线签名σ^off=e.

2) 在线签名询问：B计算k=A_I(m′－m)+r，输出在线签名σ^on=k，最后，输出此时的签名σ=(σ^on, σ^off)=(e, k).

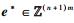
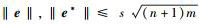
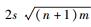
输出：A再次重复上述伪造过程中相同随机输入H和H₁询问，B返回新鲜的输出结果.由分叉引理^[14]可知，A以不可忽略的概率ε输出了1个新的有效的签名(I^*, m^*, σ^*)且. B计算A_I^*(e^*－e)=u－u=0，因为‖e‖, 且e^*≠e，所以0＜‖e^*－e‖≤，即输出e^*－e作为SIS问题的解.

概率分析：假设B能解SIS问题实例的概率为ε′，现考虑以下情形.

1) 当进行H询问时，若随机预言机H的值不匹配，将导致密钥提取询问失败，发生的概率至多为q_H/2ⁿ.因此，在密钥提取询问和签名询问阶段进行了q_E+q_S次询问之后，成功模拟的概率为

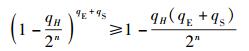
2) 当进行H₁询问时，若随机预言机H₁的值不匹配，将导致H₁询问失败，发生的概率至多为q_H1/2ⁿ.因此，在对随机预言机H₁进行了q_H1次询问之后，成功模拟的概率为.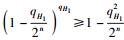

对于以上2个事件，模拟成功的概率为

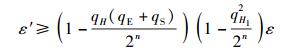
时间分析：B在模拟的过程中，只执行了哈希询问，密钥提取询问和签名询问，因此整个过程执行的时间为t′=t+q_Ht_H+(q_H1+q_S)t_H1+q_Et_ExtBasis+q_St_SamplePre，这里q(·)和t(·)分别表示执行询问的次数和执行询问的时间.

主要通过通信开销来分析新方案的性能，并将新方案与已有的方案进行了性能分析.其中，通信开销包括公钥大小、私钥大小和签名大小.具体如表 1所示.

表 1

表 1

表 1 与已有方案的性能比较

表 1 与已有方案的性能比较

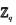
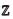
为了方便分析，统一相关参数，令l_q(q为整数)和l分别表示和上的元数的比特数.从以上分析可知，文献[13]和文献[15]的方案考虑了n个分层，假设m₁=m₂=m.文献[13]的方案整体大小较大，文献[15]的方案私钥大小较大且在线签名过程较为复杂，效率不高.而本文方案的签名过程分为离线签名和在线签名2个阶段分别来实现.与先前的方案相比，整个阶段的签名大小较小，具有更好的实现效率.

提出了一个格上基于身份的在线/离线签名方案，基于SIS困难假设，并在随机预言模型下证明了该签名方案满足适应性选择消息攻击的强不可伪造性.性能分析表明，本文方案的实现效率更高，安全性更强，具有一定的优势.另外，本文方案也可以推广到其他应用场景，如格上的门限在线/离线签名方案，格上的在线/离线重签名方案等其他特殊的方案，值得进一步深入研究.