超宽带(UWB)技术具有抗干扰性能强, 传输速率高, 通信容量大, 发送功率非常小, 结构简单, 保密性能好等优点.脉冲波形的设计是UWB系统的关键技术之一, 针对缺少满足中国辐射掩蔽的UWB脉冲设计的问题, 分析了UWB脉冲中国辐射掩蔽限制条件, 选择高斯导函数脉冲作为UWB基函数, 采用迭代算法, 设计了满足中国辐射掩蔽的UWB脉冲, Matlab数值仿真结果表明, 该组合脉冲的频谱不仅能够满足中国辐射掩蔽的要求, 而且具有较好的频谱利用率, 对于推进UWB在我国的应用具有现实的工程意义.
The ultra-wideband (UWB) technology is with strong anti-interference performance, high transfer rate, large communication capacity, small transmission power simple structure and good security performance. The pulse waveform design is one of the key technologies of UWB systems. The China radiation mask restrictions was analyzed, and the UWB pulse design method based on Gau ssian derivative function and iterative algorithm was presented for meeting with China radiation mask. The system is simulated by Matlab platform. It is shown that the spectrum of combination pulse not only meets the requirements of China radiation mask, but also has better spectral efficiency. The algorithm has practical engineering significance of promoting UWB application in China.
超宽带(UWB, ultra-wideband)脉冲通信是目前备受关注的一种新型短距离高速率无载波通信技术,利用纳秒至微秒级的非正弦波窄脉冲传输数据.
目前,频域电磁波资源已经十分拥挤,时域电磁波资源的开发及提供宽带的互联网无线接入技术具有巨大的应用前景和市场需求. UWB脉冲通信就是其中的一种,它开发出时域电磁波资源,能够和现有设备同时工作而不互相干扰.自2002年美国联邦通信委员会(FCC, federal communications commission)向民用领域开放UWB以来,关于UWB脉冲设计文献[1-9]主要是基于FCC标准.
1 中国辐射掩蔽标准目前,有3种传统的脉冲设计算法,即高斯单周期脉冲设计算法、基于扁长球体波函数的脉冲设计算法和基于改进的厄尔密特多项式脉冲算法.上述方法的功率谱密度虽然满足FCC的规定,但频谱利用率很低.近来较多是从波形的频谱利用率角度讨论超宽带脉冲波形的设计问题,提出了基于高斯脉冲各阶导函数优化组合[2008]354号文“关于发布超宽带(UWB)技术频率使用规定的通知”发布[10],在中国的UWB应用必须严格遵循其相关的要求.所以,如何选择UWB脉冲基函数,采用何种算法使得优化后的UWB成形脉冲既能满足中国辐射掩蔽标准,又能获得较高的频谱利用率,成为亟待解决的问题.
通常,UWB无线电信号与其他的无线电信号同时存在,因此可能对其他通信系统的干扰必须要限定在某一范围内,即在任一给定频率的空中接口都必须有一个最大允许功率,该功率值一般由辐射掩蔽确定.
由辐射掩蔽设定的功率极限值是相对于有效辐射功率而言的,即某一频率范围内的有效全向辐射功率(EIRP, effective isotropic radiated power),记为R,它等于发射机的最大可用功率(即发射机能够提供给天线的最大功率)和发射天线增益的乘积,即
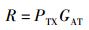
|
(1) |
其中: PTX为发射机的最大可用功率,GAT为发射天线增益.通常用dBm来表示R的大小.
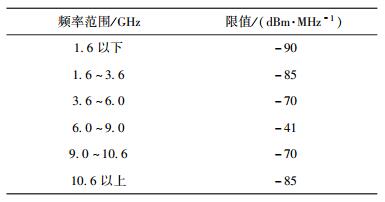
中国的辐射掩蔽标准的具体值如表 1所示.
|
|
表 1 中国UWB无线电设备发射信号的等效全向辐射功率谱密度限值[10] |
基本高斯脉冲时域表达式为
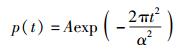
|
(2) |
其中: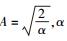
基本高斯脉冲的傅里叶变换为
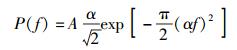
|
(3) |
n阶高斯脉冲的时域表达式为
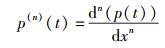
|
(4) |
n阶高斯脉冲的傅里叶变换为
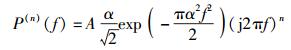
|
(5) |
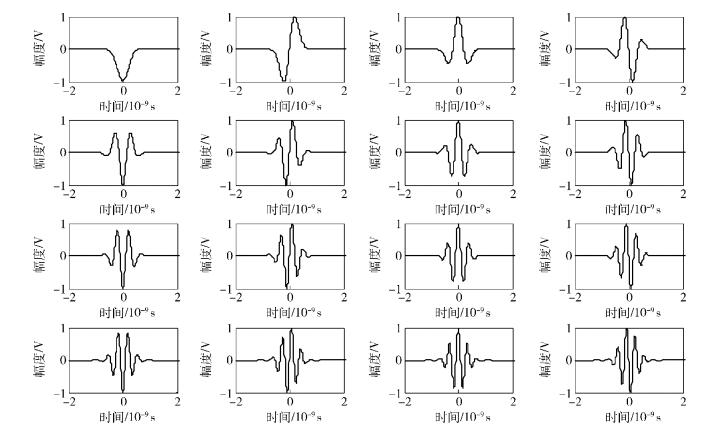
高斯脉冲和它的前15阶导函数的时域波形如图 1所示.从图 1可以看出,高斯函数的各阶导函数表示的波形都满足无直流分量的条件,脉冲宽度取决于α,减小α的值将会使脉冲宽度压缩,从而扩展传输信号的带宽.
|
图 1 高斯脉冲及其前15阶导函数的时域波形 |
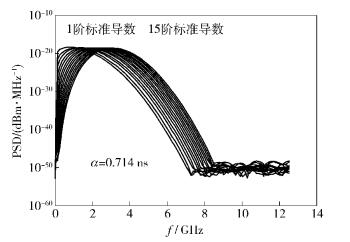
高斯脉冲微分会影响其功率谱密度,峰值频率和脉冲带宽都会随着微分数的增加而改变.对高斯函数不断求导可以得到无数个脉冲形式.高斯脉冲及其前15阶导函数脉冲的功率谱密度如图 2所示.
|
图 2 高斯脉冲和它的前15阶导函数脉冲的PSD |
从图 2可以看出,求导阶数越高,过零点数目越多,其频率越高.随着导函数的阶数升高,其功率谱密度将向频率高端移动.
脉冲产生器最容易产生的脉冲波形是一个钟形,类似于高斯函数波形.高斯函数的各阶导函数表示的波形都满足无直流分量的条件,能够有效辐射,且易于获得,所以笔者选择高斯导函数作为UWB脉冲基函数.以辐射掩蔽的符合程度作为指标,使得UWB成形脉冲的功率谱不仅满足中国辐射掩蔽标准,而且具有较高的频谱利用率.
3 满足中国辐射掩蔽的UWB脉冲设计微分和改变脉冲宽度都可以影响高斯导函数脉冲的能量谱密度,2者都可以用来形成发射波形.但单个高斯导函数脉冲的频谱不满足中国辐射掩蔽要求.
为了生成与我国UWB频谱模板相匹配的成形脉冲,使其具有现实的工程意义,仅依靠单个高斯导脉冲相当困难,笔者利用N个高斯导脉冲函数的线性组合来设计UWB成形脉冲,每个高斯导脉冲函数由给定的α值表征.对于线性组合的权重系数的选择依赖于我国UWB频谱模板要求.
UWB成形脉冲的数学表达式如下:
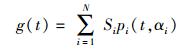
|
(6) |
其中:Si为权重系数,pi(t, αi)为第i阶高斯导函数.
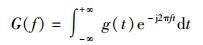
|
(7) |
即G(f)为UWB成形脉冲g(t)的傅里叶变换.
中国辐射掩蔽模板为
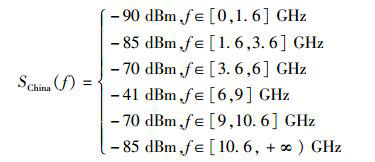
|
(8) |
则上述逼近的数学描述为
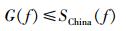
|
这样选择满足上述约束条件的Si, αi(i=1, 2, …, 15) 即可得到g(t).
选择权重系数的过程具体如下[11]:
1) 选择1组基函数;
2) 随机产生1组权重系数,记为S;
3) 检验S加权线性组合的功率谱密度是否满足中国辐射掩蔽;
4) 若在前面满足了中国辐射掩蔽的要求,并且S是第1组满足条件的系数,则设SB=S进行初始化;若前面满足了中国辐射掩蔽的要求,但过程已经初始化,则进行S与SB的比较,根据预先设定的距离度量,若S产生的波形比SB产生的波形好,则置SB=S;
5) 反复进行步骤1)~步骤3),直至所产生波形的功率谱密度与中国辐射掩蔽之间的距离在一个固定门限之下.
其中:各阶导函数的脉冲波形形成因子αi(i=1, 2, …, 15)=[1.5×10-9 0.314×10-9 0.314×10-9 0.314×10-9 0.314×10-9 0.314×10-9 0.314×10-9 0.314×10-9 0.314×10-9 0.314×10-9 0.314×10-9 0.314×10-9 0.314×10-9 0.314×10-9 0.314×10-9].
N个导函数的线性组合及其选择不同α值的可能性,给脉冲波形的产生带来了很大的灵活性.但为了保证合成函数与目标函数的差异在要求的范围内,上述算法需要经过多次迭代.
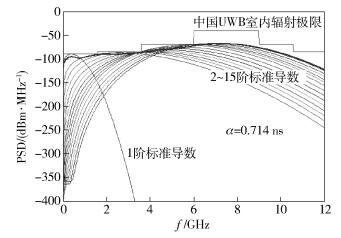
选取N个导函数的线性组合及合适的脉冲波形形成因子来得到最优波形和功率谱密度的方法如下:首先,确定中国辐射掩蔽模板SChina(f);其次,采用迭代算法选取权重系数和脉冲形成因子,使得UWB成形脉冲的功率谱G(f)最大程度地逼近模板SChina(f);最后,进行线性组合得到最优波形和功率谱. UWB成形脉冲的功率谱密度如图 3所示.
|
图 3 UWB成形脉冲的功率谱密度 |
关于UWB脉冲设计主要基于FCC标准.目前,有3种传统的脉冲设计算法,即高斯单周期脉冲设计算法、基于扁长球体波函数的脉冲设计算法、基于改进的厄尔密特多项式脉冲算法.上述方法的功率谱密度虽然满足FCC的规定,但频谱利用率很低,最高为70%左右,严重影响了系统性能.且直接套用FCC方法,不能获得满足中国辐射掩蔽标准的UWB脉冲.从图 3可以看出,笔者设计的UWB成形脉冲的功率谱(如图 3中粗线所示)不仅满足中国辐射掩蔽标准,而且具有较高的频谱利用率,频谱利用率达到81.87%,提高了系统性能.
4 结束语针对缺少满足中国辐射掩蔽的UWB脉冲设计的问题,分析了UWB脉冲中国辐射掩蔽限制条件,选择高斯导函数脉冲作为UWB基函数,采用迭代算法,设计了满足中国辐射掩蔽的UWB脉冲,Matlab数值仿真结果表明,该组合脉冲的频谱不仅能够满足中国辐射掩蔽的要求,而且具有较好的频谱利用率,对于推进UWB在我国的应用具有现实的工程意义.
| [1] | 付兴. Chirp超宽带无线通信系统中信号发生器的设计与实现[D]. 桂林: 桂林电子科技大学, 2011. |
| [2] |
陈丽丽, 于欣, 窦峥. 采用椭球波脉冲的多波段超宽带性能研究[J]. 哈尔滨工程大学学报, 2014, 35(4): 499–503.
Chen Lili, Yu Xin, Dou Zheng. Research on the performance of the multiband impulse radio UWB communication system based on PSWF[J].Journal of Harbin Engineering University, 2014, 35(4): 499–503. |
| [3] | 刘辉. 超宽带脉冲产生技术研究[D]. 西安: 西安电子科技大学, 2010. |
| [4] | 王明. 基于Chirp超宽带通信技术的研究与实现[D]. 成都: 电子科技大学, 2010. |
| [5] |
杜强, 宋耀良, 曹晓健. 基于Hermite插值滤波器的直接延时补偿超宽带波束形成技术研究[J]. 雷达学报, 2013, 2(3): 278–283.
Du Qiang, Song Yaoliang, Cao Xiaojian. Research on UWB beamforming using direct time delay compensation based on Hermite interpolation filter[J].Journal of Radars, 2013, 2(3): 278–283. |
| [6] |
赵红梅, 马琳琳, 崔光照. 一种简易的超宽带纳秒级脉冲发生器设计[J]. 现代电子技术, 2012, 35(19): 12–14.
Zhao Hongmei, Ma Linlin, Cui Guangzhao. Design of simple ultra-wideband nanosecond pulse generator[J].Modern Electronics Technique, 2012, 35(19): 12–14. doi: 10.3969/j.issn.1004-373X.2012.19.004 |
| [7] |
贾占彪, 陈红. 一种新的超宽带脉冲设计方法与性能分析[J]. 云南大学学报, 2013, 35(2): 162–166.
Jia Zhanbiao, Chen Hong. A new UWB pulse design method and performance analysis[J].Journal of Yunnan University, 2013, 35(2): 162–166. doi: 10.7540/j.ynu.20120340 |
| [8] | 刘永冲. 脉冲方式的超宽带系统的研究与设计[D]. 武汉: 武汉理工大学, 2010. |
| [9] | 刘空鹏. 室内超宽带(UWB)无线通信系统研究[D]. 浙江: 浙江大学, 2013. |
| [10] | 工信部[2008] 354号. 关于发布超宽带(UWB)技术频率使用规定的通知[Z]. http://www.xzra.gov.cn. |
| [11] |
吴珊, 吴利民, 单财良. 基于高斯脉冲的认知超宽带无线电波形设计[J]. 空军雷达学院学报, 2009, 23(4): 291–296.
Wu Shan, Wu Limin, Shan Cailiang. Design of Gaussian pulse-based CUWB radio waveforms[J].Journal of Air Force Radar Academy, 2009, 23(4): 291–296. |