2. 通信网信息传输与分发技术重点实验室, 石家庄 050081
针对单星、多终端协作定位, 提出了一种基于卡尔曼滤波的静止轨道卫星移动终端协同自主定位算法.利用同波束内的未定位移动终端进行信令交互, 获取卫星与波束中心参数进行最小二乘粗估计, 再采用卡尔曼滤波对粗估计坐标二次优化.仿真结果表明, 基于卡尔曼滤波的静止轨道卫星移动终端协同自主定位算法可在单星场景下实现较精确的终端定位, 且在协作终端数量增加时能降低定位误差的波动范围, 提高定位稳定性.
2. The Science and Technology on Information Transmission and Dissemination in Communication Networks Laboratory, Shijiazhuang 050081, China
In order to improve satellite mobile communication system's capability to carry out independent and accurate location, a satellite mobile terminals cooperative autonomous positioning algorithm based on Kalman filter(K-ACT) is proposed. Utilize unlocated user terminals in the same beam to execute signal interaction, acquire center parameters of satellites and beams through satellite broadcasting channel, and carry out Kalman filter optimization to finalize accurate coordinates. The result of simulation suggests that K-ACT algorithm is capable of realizing relatively accurate user terminal location, and fluctuation of location decreases as the number of assistant user terminals increases, resulting in higher stability of location.
近年来,随着卫星通信技术的快速发展,将长期演进(LTE, long term evolution)[1-2]技术引入卫星通信系统中,构建基于LTE的新一代卫星移动通信系统成为主流趋势[3].在该系统的研究过程中,仍然存在很多关键性问题亟须解决.随机接入技术是终端与通信网进行交互的第一步,影响整个通信过程能否顺利展开,是该系统研究的重点问题之一.在卫星移动通信系统中,卫星波束覆盖半径较大,波束中心点到波束边缘往返时延差较大,导致发送随机接入信号到达信关站的时间具有较强的不确定性[1].
笔者期望通过时延预补偿的方式降低时间不确定性,从而设置精确合理的接入时隙长度,进而节省时间资源消耗.终端位置估计作为时延预补偿的核心是笔者的研究重点.
目前,现有的卫星移动终端需要依靠导航定位(GNSS,global navigation satellite system)辅助系统进行位置估计,实现移动终端的定位[4-5].但对于静止轨道卫星来说,卫星数目较少,无法实现多颗卫星的协同定位,仅能进行粗略的位置估计,定位精度较低,误差波动范围较大,约为20~100 km[6]. Molnar等[7]提出了一种基于最小方差估计的多波束功率定位方案,但由于波束与终端间的夹角测定精度要求较高,多波束测定后的误差较大,稳定性较差.
考虑以上因素,笔者提出了一种基于增强型卡尔曼滤波的静止轨道卫星移动终端协同自主定位算法(K-ACT,satellite mobile terminals cooperative autonomous positioning algorithm based on Kalman filter). K-ACT算法的核心思想为,利用同波束内的未定位移动终端进行接收信号强度指示(RSSI,received signal strength indication)测量,通过卫星广播信道获取卫星与波束中心参数,获取协作状态下的参数集合以进行最小二乘粗优化,再采用卡尔曼滤波对粗估计坐标二次优化,最终确定终端较为精确的坐标.
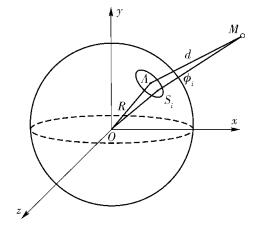
1 系统模型首先建立一个空间直角坐标系,以地心的位置作为坐标原点,然后根据卫星的广播信息确定用户所在位置周围的波束中心点坐标.具体结构如图 1所示.
|
图 1 终端协作定位空间直角坐标系 |
其中:M为卫星位置,A为波束中心点位置,Si为移动终端位置,d为卫星到波束中心点的距离,对于不同的波束,d值也是不同的,ϕi为用户到卫星的连线与卫星到波束中心点连线之间的夹角.
在图 1中,波束中心点与移动终端的接收功率强度比值是与ϕi变量相关的函数,可用一个指数模型[7]描述为
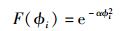
|
(1) |
其中:F(ϕi)为卫星波束中心点与移动终端接收信号辐射强度的关系比值,α可选择一个适合实际波束形状的值,为一个经验参数,由海事卫星实际测量的结果取值.
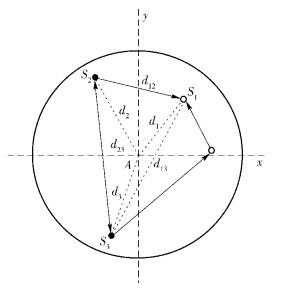
地面移动协作终端的通信过程可建立模型,如图 2所示,其中S1为目标终端,S2、S3为协作终端.
|
图 2 波束中心与终端位置关系平面示意图 |
考虑卫星通信单波束覆盖范围较大这一特点,单跳协作机制具有一定的局限性,因此笔者通过广播信道(BCH,broadcast channel)获取协作节点定位参数,并采用WHTDV-HOP算法测量协作节点在多跳场景时的RSSI信息[8].针对如何减小测距误差,Yi等[9]证明采用RSSI模型测量位置节点之间的距离可有效减少其测距误差,基于此思想,笔者采用Log-Normal Shadowing模型[10]为

|
(2) |
其中:Pij为协作终端到未知节点的接收功率,P0为协作终端发射功率,dij为终端间距离,vij为独立同分布的随机变量,考虑多径的影响,有vij~N(μ, σv2),μ为测距误差,σv为根据实际环境设置的标准差.
2 K-ACT定位算法2.1 算法概述协作位置估计的意义在于寻找各未知节点相互满足某种条件的参数估计,即构造一个未知节点坐标的函数作为被估计量的一个无偏估计.数据滤波是去除噪声还原真实数据的一种数据处理技术,在基于卡尔曼滤波的协作终端定位方案中,最核心的工作就是根据测量值重构系统的状态参数值,在循环迭代中不断更新状态参数值,即位置坐标协方差和卡尔曼滤波增益,以“实测—估计—修正”的顺序递推,根据测量值消除随机干扰,再现系统的状态.
2.2 算法分析K-ACT定位算法需要由未知节点获取的信息来源分为2部分:第1部分为卫星与波束中心点的信息;第2部分为协作节点的相关信息.首先,未知节点可测量卫星到本节点的接收功率Pi,并通过卫星的BCCH信道获取波束中心点的接收功率P0以及卫星与波束中心点的坐标.由此可得到终端与波束中心点的功率比值Fi=Pi/P0.其次,未知节点选定可参与协作定位的协作节点S1,S2,…,Sn,并测量协作节点到达未知节点的接收功率Pij,获取由协作节点广播得到的相对波束中心点的功率比值Fj, j≠i以及协作节点之间的测距信息dij.
未知节点根据周围可参与协作节点的多少计算多组坐标值,并通过最小二乘估计算法对坐标进行粗优化,降低噪声对坐标值计算带来的波动.随后利用卡尔曼滤波算法计算协方差位置增益,再次精确未知节点坐标值,更新坐标信息.最后,通过判断协方差增益是否满足收敛门限的判决条件(Hk<m)决定重复定位估计或确定位置坐标.
各协作用户相对波束中心点的功率比值Fi可由式(1) 进行以下变换
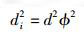
|
(3) |
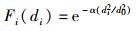
|
(4) |
周围协作节点可获取与波束中心点的相对功率比值Fj,利用指数模型可得
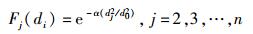
|
(5) |
在式(2) 和式(3) 中,只有di, dj为未知数,因此可联立方程组求解终端位置的坐标.
假定对第i个用户进行定位,则根据协作终端个数的不同(n≥3) 可列方程,并代入具体坐标得
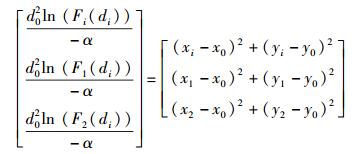
|
(6) |
根据协作节点间RSSI测距后的结果,建立协作节点与未知节点的坐标关系式为

|
(7) |
联立式(6) 和式(7),可求得S1,S2,Si 3点的初始坐标.同理可得Sm,Sn,Si的初始坐标.并通过最小二乘估计算法降低Si的坐标波动幅度,坐标样本值越多,估计值越精确.
当未知终端计算出n组坐标值(xi1, yi1), …, (xin, yin)之后,预得到坐标Si(xi, yi),使得M(x, y)=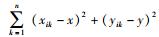
因受噪声的影响,功率值不断波动,以致计算得到的未知节点位置也在波动.所以,选用卡尔曼滤波算法进行坐标优化.下面结合计算出的位置坐标的协方差来估算系统的最优化输出.
首先利用系统的过程模型,来预测下一状态的系统.假设现在的系统状态为k,根据系统模型,可基于系统的上一状态预测现在状态为
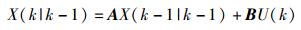
|
(8) |
其中:U(k)为系统控制量,X(k|k-1) 为利用上一状态预测的结果,X(k-1|k-1) 为上一状态最优的结果,由于本系统的定位终端与协作终端的位置与上一时刻相同,故A=1且无控制量,故U(k)=0.因此,X(k|k-1)=X(k-1|k-1),即上一状态的最优结果就是对上一状态的位置预测结果.
式(8) 表示了对定位结果的更新,下面更新位置协方差H为
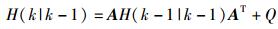
|
(9) |
其中:H(k|k-1) 为X(k|k-1) 对应的协方差,H(k-1|k-1) 为X(k-1|k-1) 对应的协方差,AT为A的转置矩阵,Q为系统过程噪声的协方差.由于A=1,故
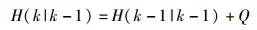
|
(10) |
根据k状态下的预测结果以及k状态下的测量值,可通过计算得到当前状态的最优化估算值为
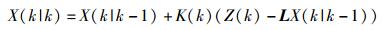
|
(11) |
其中:K为卡尔曼增益(Kalman Gain),Z(k)是k时刻的测量值.
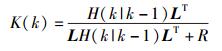
|
(12) |
R为系统测量噪声,在得到k状态下最优的估算值X(k|k)后,更新k状态下X(k|k)的协方差H(k|k),以便卡尔曼滤波器不断地运行直到系统过程结束.
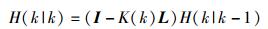
|
(13) |
其中:I为单位矩阵,对于单模型单测量,I=1.当系统进入k+1状态时,H(k|k)为式(9) 的H(k-1|k-1).直到协方差增益H小于系统收敛判决门限m时,系统将输出当前估计坐标值作为系统定位坐标.
3 仿真分析仿真的目的是验证基于卡尔曼滤波的卫星移动终端协同定位算法的性能,主要包括2方面内容:
1) 定位算法的收敛过程与MVE算法[7]的对比分析;
2) 定位精度以及波动性与MVE算法[7]和GMR标准[6]的对比分析.
主要参数设置如下:波束半径为150 km,α=2.891×10-5,终端发射功率为5 dBW,环境噪声和测量系统噪声功率分别为0.1 dB.
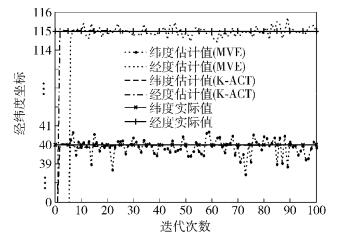
1) 定位算法的收敛过程与MVE算法[7]的对比分析(见图 3).
|
图 3 定位算法的收敛过程仿真对比 |
由图 3可知,笔者提出的K-ACT算法随着迭代次数增加,终端位置坐标的估计值逐渐向实际值靠拢,在第3次迭代后稳定在实际值附近,波动范围较小(小于200 m),估计值与实际值基本重合. MVE算法在第5次迭代后趋于平稳,并在实际值附近波动,但其波动范围较大,约为10 km左右.由此可见,基于卡尔曼滤波的移动终端协作定位算法可以实现精确定位功能.
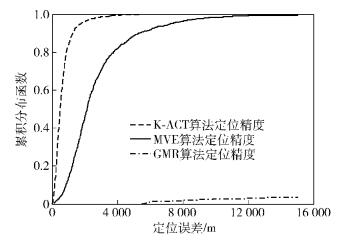
2) 定位精度以及波动性与MVE算法[7]和GMR标准[6]的对比分析(见图 4).
|
图 4 定位精度以及波动性的仿真对比 |
图 4仿真对比分析了K-ACT算法(2个协作节点)与MVE算法[7]以及GMR标准[6]中的功率定位算法的定位精度以及波动性.由图 4可知,K-ACT算法的定位精度最高,波动性最低,GMR算法的定位精度以及稳定性最差. K-ACT算法的定位误差在1 km之内的概率为80%,2 km之内的概率为100%;MVE算法的定位误差在2 km之内的概率为50%,5 km之内的概率为88%,10 km之内的概率为98%;GMR标准的定位精度大约在50~80 km.
K-ACT算法较MVE算法在定位精度方面由10 km波动范围降低至2 km,其主要原因为,终端协作定位首先利用的是协作节点与未知节点的距离关系进行定位,由于协作节点与未知节点在同一个波束内,终端测距的误差远远小于通过卫星功率比测距的误差,而MVE算法需要测定周围6个波束中心点与未知节点的接收功率比,这就增大了定位所需的测距误差,较大的测量误差会导致定位精度大幅下降.此外,K-ACT算法可通过增加协作节点的数量来提升坐标估计的稳定性,这是由于K-ACT算法在计算初始坐标之前预先通过最小二乘优化方法,将多个初始坐标值进行预处理,降低了单次测量引起的坐标波动范围.通过以上仿真分析可知,K-ACT算法在定位精度与稳定性方面均较先前的研究有明显提升.
4 结束语针对GEO通信卫星自主定位精度较低、稳定性较差的问题,结合下一代卫星通信系统的特点,提出了基于卡尔曼滤波的移动终端协同定位算法.分析比较了本文算法与MVE算法以及GMR标准的功率定位方案的性能优劣,由仿真结果可知,笔者提出的K-ACT算法可有效改善定位精度较低、定位波动范围较大的问题.值得一提的是,笔者针对的是下一代GEO卫星移动通信系统,其中涉及的协同定位方案需要基于较完备的卫星移动终端协作技术.在当前协作技术飞速发展的环境下,对未来通信卫星自主定位提供了较为可靠的研究方向与理论依据.
| [1] | 3GPP TS 36.201 V10.0. Evolved universal terrestrial radio access (E-UTRA); LTE physical layer; General description[S]. |
| [2] | Recommendation ITU-R M. 2012. Detailed specifications of the terrestrial radio interfaces of international mobile telecommunications advanced[R]. 2012. |
| [3] | 汪春霆, 张俊祥, 潘申富, 等. 卫星通信系统[M]. 北京: 国防工业出版社, 2012. |
| [4] |
吴鹏, 刘文祥, 王飞雪. GNSS应急辅助定位及精度评估方法研究[J]. 国防科技大学学报, 2013, 35(4): 140–145.
Wu Peng, Liu Wenxiang, Wang Feixue. GNSS emergency positioning method and research on the accuracy estimation[J].Journal of National University of Defense Technology, 2013, 35(4): 140–145. |
| [5] |
戴连君, 唐涛, 蔡伯根, 等. 基于北斗卫星载波相位平滑伪距的列车定位方法[J]. 铁道学报, 2012, 34(8): 64–69.
Dai Lianjun, Tang Tao, Cai Bogen, et al. Method of train positioning based on Beidou carrier phase smoothing code[J].Journal of the China Railway Society, 2012, 34(8): 64–69. |
| [6] | GMR-1 05. 008 (ETSI TS 101 376-5-6): "GEO-mobile radio interface specifications; part 5: radio interface physical layer specifications; sub-part 6: radio subsystem link control"[S]. 2005. |
| [7] | Molnar K J, Dent P W. Terminal position location using multiple beams: U. S. Patent 6, 684, 071[P]. 2004-01-27. |
| [8] |
周玲, 康志伟, 何怡刚. 基于三角不等式的加权双曲线定位DV-HOP算法[J]. 电子测量与仪器学报, 2013, 27(5): 389–395.
Zhou Ling, Kang Zhiwei, He Yigang. Weighted hyperbolic positioning DV-HOP algorithm based on triangle inequality[J].Journal of Electronic Measurement and Instrumentation, 2013, 27(5): 389–395. |
| [9] | Yi Tingting, Fang Zhiyi, Li Ruixue. RMADV-HOP: an improved DV-HOP localization algorithm[C]//Information Technology: New Generations (ITNG), 2010 Seventh International Conference on. IEEE, 2010: 939-943. |
| [10] | Li Xinrong. Collaborative localization with received-signal strength in wireless sensor networks[J].Vehicular Technology, IEEE Transactions on, 2007, 56(6): 3807–3817. doi: 10.1109/TVT.2007.904535 |


