为了分析控制器位置和控制消息路由树对软件定义网络控制平面性能(如控制消息平均时延、控制消息路由树可靠性)的影响, 建立相关数学模型, 提出启发式的路由树搜索算法、最短路径算法和贪婪算法并对该模型进行优化.仿真结果显示, 在相同的网络拓扑条件下, 启发式路由树搜索算法能有效地在控制消息平均时延和控制消息路由树可靠性2个性能指标上取得均衡, 其综合性能明显优于最短路径算法和贪婪算法.
For analyzing the impact of both controller location and control messages routing tree on the performance of software-defined networking control plane (e.g. the average latency of control messages, the routing tree reliability), the corresponding mathematical model was built, and three algorithms, which are the heuristic routing tree algorithm, the shortest path algorithm and greedy algorithm, were also proposed to optimize the model for this controller placement problem. The evaluation results show that the proposed heuristic routing tree algorithm achieves a trade-off between control messages average latency and routing tree reliability, and obviously performs better than the shortest path algorithm and greedy algorithm.
当前,软件定义网络(SDN, software-defined networking)[1-2]中的控制器放置问题引起了学术界的广泛关注.相关文献已经对广域网中的SDN控制器放置问题进行了深入研究[3-6].然而,现有的研究工作多数基于SDN控制平面网络和数据平面网络在物理上独立组网的模式,但在实际部署中通常采用带内(in-band)组网模式,即控制平面的流量和数据平面的流量共享相同的底层物理链路.这是由于为传输少量的控制平面流量而组建独立的控制平面网络成本过高,尤其在广域网部署中,节点间的距离通常很远造成的.笔者的研究背景与文献[7]相同,即满足以下3个条件:① 在SDN实际部署中采用带内组网模式;② 控制器位置限定在所有可能的交换机位置上,忽略控制器到其所在位置节点间的路径时延;③ 控制器与交换机间只存在一条可用路径.但相比于文献[7],笔者所关注的问题是如何寻找最佳的控制器位置和控制消息路由树,尽可能地优化控制消息平均时延和控制平面路由树的可靠性.
1 数学模型定义网络拓扑G=(V, E, Wl, Wp)①,其中V为节点集合,E为链路集合,Wl为链路的时延权重,Wp为链路的可靠性权重. 表 1给出了所有定义变量的含义.
① 为不失一般性,文中拓扑链路的时延权值和可靠性权值分别服从区间为[1.00, 10.00]和[0.950, 1.000]的平均概率分布.
|
|
表 1 控制器放置数学模型参数说明 |
对于给定控制器位置,不同路由树生成算法可以构建不同的路由树.如图 1所示,虚线代表所有的网络链路,圆圈代表所有的网络节点,矩形框代表控制器放置的位置,实线代表控制消息的路由树.该控制器放置问题可描述为
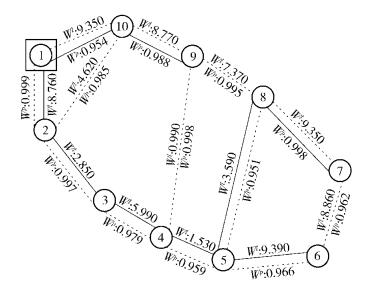
|
图 1 Internet 2拓扑中控制器位置与路由树选择示例 |
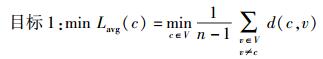
|
(1) |
|
(2) |
为优化上文所述的平均时延和可靠性指标,本节提出了3种优化算法,分别是启发式的路由树(HRT, heuristic routing tree)算法、最短路径算法和贪婪算法.其中,HRT算法兼顾平均时延和路由树可靠性指标,并返回Pareto最优解集合;最短路径算法只能优化单一目标,如基于链路时延权重优化控制消息平均时延,或者基于链路可靠性权值优化路由树的可靠性;贪婪算法同样可基于链路的权重优化单一目标,但相比于最短路径算法,该算法可降低计算复杂度.
2.1 HRT生成算法HRT生成算法搜索控制器的位置以及控制消息路由树的解空间,并返回可在平均时延和可靠性间取得最佳均衡的解集合.算法定义集合X={x0, x1, …, xn},其中参数x0为控制器位置的序号,xi(i>0) 为控制器x0到节点i之间的路径序号.对于任一给定的向量X,x0为控制器的位置,路由树可由控制器位置x0到所有节点的路径{x1, x2, …, xn}②通过去除冗余链路构建. 表 2给出了详细的参数解释.
② 当控制器位置与节点位置重合时,即x0=i时,xi无意义.
|
|
表 2 HRT生成算法参数说明 |
在算法初始化阶段,随机生成种群规模为s的初始种群,采用二进制锦标赛选择、重组以及变异进化种群,并通过非占优排序生成下一代种群.算法通过迭代不断改进种群质量,直至种群代数达到预先规定值.为应用HRT生成算法,式(1) 和式(2) 需改写为
|
(3) |
|
(4) |
约束条件:
|
(5) |
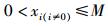
|
(6) |
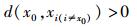
|
(7) |
在HRT算法执行之前,需先将控制器到节点路径信息(时延和可靠性)存储在4维数组Array[|V|][|V|][M][|V|-1]中,该数组的第1维代表控制器位置,第2维代表节点位置,第3维代表路径编号,第4维代表该路径上的链路编号.从而,对于任一控制器到节点的路径,其上的链路时延和链路可靠性信息是完备的.
下面给出HRT算法的主要流程.算法1~2步是初始化流程,主要包括目标函数、初始种群规模、初始种群个体以及最大种群代数等参数设定.第3步是根据初始种群通过二进制锦标赛选择、重组和突变产生同等规模的新种群.第5~17步是算法的主循环,每一代的精英个体通过非占优排序和拥塞比较排序得以保存到下一代中[8].具体方法是,首先将种群Pj和Qj合并,再对合并过后的种群进行非占优排序得到F={F1, F2, F3, …, Fn},随后在排序后的结果F中选择前s个个体作为下一代种群.假设Fi是最后一个非占优前沿集合,排在Fi之后的种群不会被选择.通常,F1到Fi集合的总数量不会恰好是s.因而,需对非占优前沿集合Fi基于拥塞比较进行排序,选择排序后的Fi中的前一段使得下一代种群规模恰好为s.上述迭代过程一直重复直至种群规模达到指定的代数.值得注意的是,最后的种群需要进行校验,将成环的路由树从Pg中剔除,以确保控制消息的路由转发不会形成环路.
HRT算法流程:Heuristic_Routing_Tree (G=(V, E, Wl, Wp), Array[|V|][|V|][M][|V|-1])
1. 设置目标函数:目标1为控制消息平均时延,目标2为路由树可靠性
2. 设置初始种群规模大小为s,随机生成初始种群P0,其中任一个体由集合X={x0, x1, …, xn}表示,且最大种群代数为g
3. Q0=make-new-population(P0) // Q0由种群P0通过二进制锦标赛选择、重组和突变产生
4. j=0
5. while(j<g)
6. Rj=Pj∪Qj
7. F=fast-non-dominated-sort(Rj) //对Rj进行非占优排序得F={F1, F2, F3, …, Fn}
8. Pj+1=∅, i=1
9. while(|Pj+1|+|Fi|<s)
10. Pj+1=Pj+1∪Fi
11. i=i+1
12. end while
13. 对Fi采用基于拥塞比较操作符∧i的排序
14. Pj+1=Pj+1∪Fi[1:(s-|Pj+1|)]
15. Qj+1= make-new-population(Rj+1)
16. j=j+1
17. end while
18. 校验Pg中任一个体,将成环的个体从Pg中剔除
2.2 最短路径算法1) 基于链路时延最短路径(LSP, latency-based shortest path)算法.控制消息路由树通过基于时延的最短路径算法构建,其根节点为控制器位置.为寻求最佳控制器位置以及相应的控制消息路由树,LSP算法遍历所有可能的控制器位置,并通过最短路径算法计算控制器到其他节点的时延最小路径.该算法输入为G=(V, E, Wl, Wp),输出为最佳控制器位置和相应的控制消息路由树Tc,使得控制器消息平均时延最小.
LSP算法流程:Latency_Shortest_Path (G=(V, E, Wl, Wp))
1. for c∈V
2. 初始化路由树Tc=∅,控制消息传输总时延Lc=0
3. 采用Dijkstra算法计算控制器位置c到所有其他节点的最短路径
4. 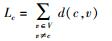
5. 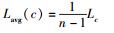
6. end for
7. 选择使控制消息平均时延最小的控制器位置c,以及相应的路由树Tc
2) 基于链路可靠性的最大路径(RLP, reliability-based largest path)算法. RLP算法的主要流程与LSP算法类似,其主要区别在于:① 选择控制器到节点具有最大可靠性的路径,而非最小时延路径;② 路由树可靠性R(c)由式(2) 得出;③ 依据路由树可靠性最大原则选择最佳控制器位置和相应路由树Tc.
2.3 贪婪算法1) 基于链路可靠性的贪婪算法(RGA, reliability-based greedy algorithm).最短路径算法构造路由树需要计算控制器到其他节点的最短路径,当网络规模较大时,此算法的计算复杂度很高.因此,提出RGA,该算法利用当前节点与邻居节点间的链路连接关系,依次选择最佳的链路构成路由树.
在RGA中,集合N存储路由树的节点,集合Ec存储路由树的链路,集合Sv表示节点v的所有邻居节点,集合Uv表示属于集合Sv但不属于集合N的节点.算法的初始化阶段,控制器位置c被加入到集合N中,且设置集合Ec为空集.在第i(i<n)次迭代中,显然易得节点v的邻居节点Sv,结合集合N可得出Uv.若Uv不为空,则选择Uv中的某一节点,使得该节点与节点v之间的链路可靠性最大.反之,若Uv为空,则逆序遍历集合N中的节点,直至满足条件|Uv|>0.重复上述过程直至|N|=n.算法的输入为带权重的网络拓扑G=(V, E, Wl, Wp),输出为使得路由树可靠性R(c)最大的控制器位置c以及相应的路由树Tc.
RGA流程:Reliability_Greedy_Algorithm(G=(V, E, Wl, Wp))
1. for c∈V
2. 初始化N={c},Ec=∅以及v=c
3. while (|N|<n)
4. Sv为节点v的邻居节点集合
5. Uv=Sv\N
6. if (|Uv|>0)
7. for u∈Uv
8. 选择节点u使得链路ev→u可靠性最大
9. end for
10. N=N∪{u}, Ec=Ec∪{ev→u}
11. end if
12. else
13. 逆序遍历集合N中的节点,直至|Uv|>0
14. end else
15. end while
16. end for
17. 计算路由树的可靠性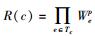
2) 基于链路时延的贪婪算法(LGA, latency-based greedy algorithm). LGA和RGA的算法流程类似,其主要区别在于:① 以链路时延权值最小作为选择标准;② 依据路由树Tc计算控制消息平均时延Lavg(c);③ 选择使得控制消息平均时延Lavg(c)最小的控制器位置c以及路由树Tc.
3 仿真分析在本节中,设计一些实验来评估HRT算法、最短路径算法和贪婪算法的性能.第1个实验采用Internet 2拓扑,链路时延权值以及可靠性权值分别服从区间为[1.00,10.00]和[0.950, 1.000]的平均概率分布.如图 2(a)所示,横坐标是平均时延性能指标(见式(3)),纵坐标是故障率指标(见式(4)),其中圆圈显示的是HRT算法得出Pareto最优解的性能结果.同时,对于任一控制器的位置,图 2(a)也显示了采用最短路径算法与贪婪算法得出的最佳解的性能指标结果. 图 2(b)和图 2(c)分别显示了上述实验在的Quest和OS3E拓扑上的实验结果.上述3个分图所采用的拓扑分别代表典型的小型、中型以及大型的广域SDN部署场景.
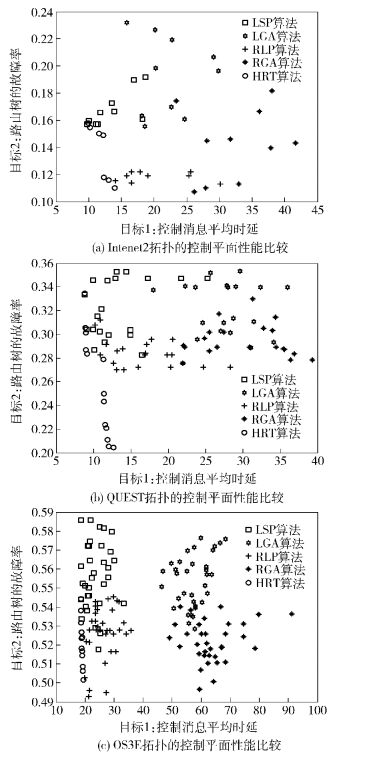
|
图 2 控制平面性能 |
由图 2可得3个结论. ① LSP算法的平均时延指标性能最佳,但其可靠性指标较差. RLP算法和RGA算法的可靠性指标要优于LSP算法和LGA算法,但是前者的平均时延指标要比后者差.这是由于多个指标间通常是互相冲突的,最短路径算法和贪婪算法均难以同时优化多个目标.上述算法中,只有HRT算法能很好地在平均时延指标和可靠性指标间取得均衡. ② HRT算法提供多个非占优解,且均在平均时延和可靠性上保持较好的性能指标.这是因为在算法迭代过程中,优良的个体通过非占优排序被保留到子代中,同时个体的交叉、变异操作,以及排序中采用拥挤度和拥挤度比较算子使种群的多样性得以保证. ③ 随着网络拓扑规模的增大,2个优化目标的性能明显下降,尤其是可靠性指标.这是由于控制器到其他节点路径的时延随着网络规模的扩大而增加,此外路由树可靠性也由于链路增加而降低,这也间接说明一个控制器往往难以管控一个大型网络.
通常网络设计者仅仅关心图 2中左下角圆圈所示结果,即HRT算法的Pareto最优解集合. 图 3显示的是HRT算法基于Internet 2网络在一次实验中的Pareto最优解的结果.其中,横坐标代表的是控制消息平均时延指标,纵坐标代表的是路由树的故障率. 图 3中所示的Pareto最优解要么在其中某一指标上全局最优(如果存在的话),要么是在两者中保持较好的均衡,网络设计者可根据实际需求的优化目标偏向选择其中某些Pareto最优解.
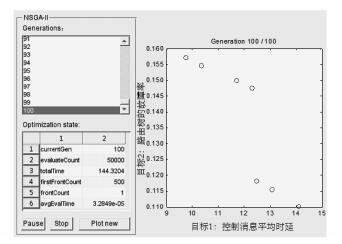
|
图 3 Internet2拓扑的Pareto最优解 |
控制器放置问题是当前SDN领域中的研究热点,但相关研究对于SDN带内组网模式缺乏足够的重视.笔者首先调研带内组网在实际广域SDN部署存在的优势,并分析量化控制器位置以及路由树对SDN控制平面性能(如控制消息平均时延和控制平面的可靠性)的影响.然而,由于控制消息平均时延指标与控制平面可靠性指标间存在冲突,二者通常不可能同时达到最优.笔者进一步提出了HRT算法,提供给网络设计者所有可能的Pareto最优解集合.仿真结果表明,HRT算法较好地在控制消息平均时延和控制平面可靠性指标上取得均衡,其性能明显优于最短路径算法和贪婪算法.
| [1] | Mckeown N, Anderson T, Balakrishnan H, et al. Openflow: enabling innovation in campus networks[J].ACM SIGCOMM Computer Communication Review, 2008, 38(2): 69–74. doi: 10.1145/1355734 |
| [2] | Mendonca M, Astuto B N, Nguyen X N, et al. A survey of software-defined networking: past, present, and future of programmable networks[J].IEEE Communications Survey and Tutorials, 2014, 16(3): 1617–1634. doi: 10.1109/SURV.2014.012214.00180 |
| [3] | Heller B, Sherwood R, Mckeown N. The controller placement problem[C]//Proceedings of the First ACM SIGCOMM Workshop on Hot Topics in Software Defined Networks. Helsinki, Finland: [s.n.], 2012: 7-12. |
| [4] | Bari M F, Roy A R, Chowdhury S R, et al. Dynamic controller provisioning in software defined networks[C]//IEEE/ACM/IFIP International Conference on Network and Service Management (CNSM). Zurich, Switzerland: [s.n.], 2013: 18-25. |
| [5] | Hu Yannan, Wang Wendong, Gong Xiangyang, et al. On reliability-optimized controller placement for software-defined networks[J].Communications, China, 2014, 11(2): 38–54. doi: 10.1109/CC.2014.6821736 |
| [6] | Hock D, Hartmann M, Gebert S, et al. Pareto-optimal resilient controller placement in SDN-based core networks[C]//IEEE 25th International Teletraffic Congress (ITC). Shanghai, China: [s.n.], 2013: 1-9. |
| [7] | Beheshti N, Zhang Ying. Fast failover for control traffic in software-defined networks[C]//IEEE Global Communications Conference (GLOBECOM). Anaheim, CA, USA: [s.n.], 2012: 2665-2670. |
| [8] | Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182–197. doi: 10.1109/4235.996017 |