针对两单播多跳网络, 在存在两个中继端的情况下, 研究源端的干扰对齐预编码设计、中继的干扰消除解码和预编码转发设计, 以及目的端的干扰消除解码处理.对干扰对齐和解码需满足的约束条件进行分析, 给出简化的网络干扰对齐的可行条件.此外, 对源端与中继端的功率分配进行优化.最后对干扰对齐的可行性、功率分配的性能进行仿真测试.表明在满足网络对齐约束条件后, 干扰对齐可行, 并且采用简化迭代注水功率分配算法较采用平均功率分配算法的系统容量有明显提高.
Considering the 2-unicast problem with multiple hops and two relays, research the interference alignment precoding matrixs at the sources, the interference elimination decoding and precoding forward at the relays, and interference cancellation decoding at the destinations are researched. The simplified feasible conditions of network interference alignment were given based on the analysis of constraints of network interference alignment and decoding. In addition, the power allocation of relays and sources are optimized. Simulation tests of the feasibility of interference alignment shows a good performance of the power allocation. And it is shown that interference alignment is feasible if conditions were satisfied, and the system capacity is significantly improved when the simplified water filling power allocation algorithm is used when comparing with the average power allocation algorithm.
目前单播是无线和有线网络的主要传播形式,对于单播网络的干扰问题,Ramakrishnan等[1-3]联合应用干扰对齐技术与网络编码[4]技术,设计特殊的预编码矩阵,并给出实现网络对齐的约束条件.
由于网络越复杂,预编码、解码等处理越复杂,不便于对算法进行描述,因此针对两单播网络,在文献[1]和文献[5]的基础上研究有2个中继的情况下,源端的预编码、中继的解码与编码转发、目的端的解码处理方案,并分析网络干扰对齐和解码成功需满足的约束条件.进一步,结合单播网络干扰对齐方法和注水功率分配方法对源端和中继端发射功率分别进行功率分配,以达到容量优化的目的.预编码、解码、功率分配等算法的原理和方法也可以运用于更复杂网络中,让网络干扰对齐成功运用于多单播网络中,提高网络性能.
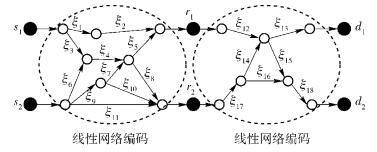
1 网络模型研究一个两单播的多跳网络,如图 1所示. 图 1中,s1,s2为源端,d1,d2为目的端,r1,r2为中继.源端与中继、中继与目的端之间的网络为单播网络,除了中继r1,r2,所有其他中间节点只是执行随机线性网络编码操作. di期望收到si发送的信息,网络中每条边的容量为1,每个源端发送的信息相互独立.这里把这个网络统称为两大跳网络,虚线椭圆内为每跳中的网络.
|
图 1 网络模型 |
设Hji, 1表示从源端si到中继端rj的传输矩阵,Hji, 2表示从中继ri到目的端dj的传输矩阵.若进行m的符号扩展,则Hji, 1与Hji, 2为m×m的对角矩阵.参照图 1的示例,第1跳由传输矩阵构建的分块矩阵为
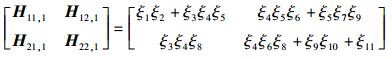
|
(1) |
同样地,第2跳由传输矩阵构建的分块矩阵为
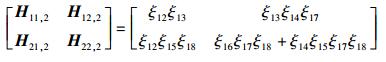
|
(2) |
其中:ξi为编码系数,不同的网络,传输矩阵不同.
假设si为发端i(源端和中继端)的发送向量,发送向量的大小为wi.在发端进行功率分配和预编码处理,Pi为功率分配对角矩阵,Vi为预编码处理矩阵,Hji为发端i到收端j的传输矩阵.假设收端接收到的噪声nj为零均值复高斯白噪声,协方差矩阵为σ2Iwi.在发端当i=1, 2时,wi分别为m、m-1.
在收端(中继端和目的端)j接收的信息为
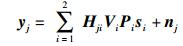
|
(3) |
其中: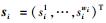
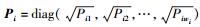
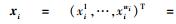
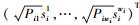
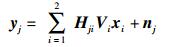
|
(4) |
设源端s1,s2在功率分配后发送向量为x1,x2.由以上可知,中继r1,r2接收到的信息为
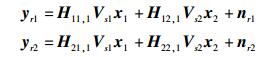
|
(5) |
为保证每个用户有足够的空间进行干扰对齐,进行m的符号扩展,源端预编码矩阵Vs1,Vs2分别为m×m、m×(m-1) 的矩阵.相应Hji, 1为m×m的对角矩阵.利用文献[6]的对齐方法进行预编码,设Vs1= [vs1, 1, vs1, 2, …, vs1, m],Vs2=[vs2, 1, vs2, 2, …, vs2, m-1]表示在源端s1,s2的预编码矩阵,在中继端r1,H11, 1vs1, l+1和H12, 1vs2, l对齐,在中继端r2,H21, 1vs1, l和H22, 1vs2, l对齐
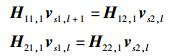
|
(6) |
其中:l=1, 2,…,m-1,vs1, 1=[1, 1, …, 1]T为m×1的向量,则
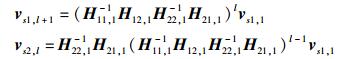
|
(7) |
如此,将式(6)、式(7) 代入式(5) 可得
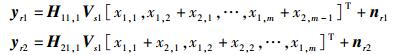
|
(8) |
在中继端ri对接收到的信号yr1,yr2分别左乘矩阵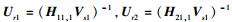
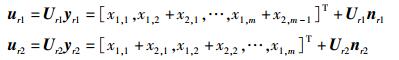
|
(9) |
由于传输矩阵的相关性,为了干扰对齐及解码可行,H11, 1,H21, 1,H12, 1,H22, 1,H11, 1Vs1,H21, 1Vs1需可逆.
2.2 中继端到目的端的处理在中继转发过程中,中继ri发送向量为ui=Priuri,Pri为ri的功率分配矩阵.若中继端与源端采取同样的预编码方法,由式(8) 可知,目的端接收到的都为x1,x2的混合信号.干扰对齐及解码可行取决于传输矩阵,若中继端的预编码矩阵进行适当的变换,不仅可以解决无法解码的问题,还可减轻目的端的解码复杂度,使约束条件更加简化.传输矩阵为对角矩阵,由其构成的分块矩阵的逆也为对角矩阵构成的分块矩阵,即
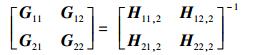
|
用对应的逆矩阵进行预编码,设
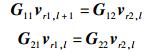
|
(10) |
则
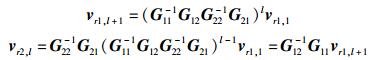
|
(11) |
且设计在中继端最终发送的信号为
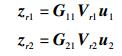
|
(12) |
则目的端接收的信息为
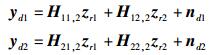
|
(13) |
将zr1,zr2的表达式(12) 代入式(13),得到
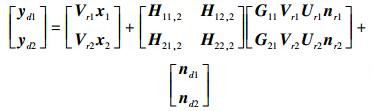
|
(14) |
在目的端d1,d2对接收信息yd1,yd2分别左乘Ud1,Ud2即可解码出x1,x2,其中Ud1=Vr1-1,Ud2=(Vr2TVr2)-1Vr2T.如此,要解码成功,H11, 2,H12, 2,H21, 2,H22, 2,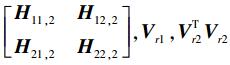
由2.1、2.2可知,要干扰对齐可行且解码成功, H11, 1,H21, 1,H12, 1,H22, 1,H11, 1Vs1,H21, 1Vs1,H11, 2,H12, 2,H21, 2,H22, 2,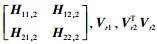
1)H11, 1,H21, 1,H12, 1,H22, 1,H11, 2,H21, 2,H12, 2,H22, 2可逆:若det (H11, 1H21, 1H22, 1H12, 1)≠0,则H11, 1,H12, 1,H21, 1,H22, 1可逆.同理,det (H11, 2H21, 2H22, 2H12, 2)≠0,则H11, 2,H21, 2,H12, 2,H22, 2可逆.
2)H11, 1Vs1,H21, 1Vs1可逆:令H11, 1-1H12, 1H22, 1-1H21, 1=diag(M1, M2, …, Mm),若要det (H11, 1Vs1)≠0,只需det (H11, 1)det (Vs1)≠0,又因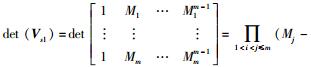
3) 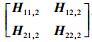
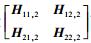
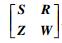
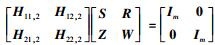
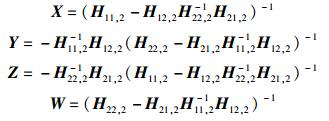
|
(15) |
若要X, Y, Z, W都存在,只需
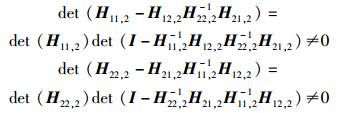
|
(16) |
设N=H11, 2-1H12, 2H22, 2-1H21, 2=diag(N1, N2, …, Nm),又传输矩阵皆为对角矩阵,只要det (I-N)≠0且det (H11, 2H21, 2H21, 2H22, 2)≠0,则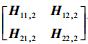
4)Vr1可逆:因为G11-1G12G22-1G21=X-1YZ-1W=H11, 2-1H12, 2H22, 2-1H21, 2=N,则det (Vr1)= 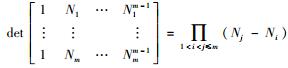
5)Vr2TVr2可逆:若需Vr2TVr2可逆,则rank(Vr2TVr2)=m-1,又因为rank(Vr2TVr2)=rank(Vr2T)=rank(Vr2),由式(11) 可知,若rank(Vr1)=m, 则rank(Vr2)=m-1,如此转化为Vr1可逆,即Nj≠Ni(i < j), 则Vr2TVr2可逆.
由以上过程可知,要整个网络进行干扰对齐且解码成功,需满足的条件可整理为
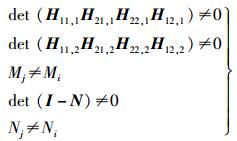
|
(17) |
由于采用符号扩展的方法,即对角元素是时变的,所以式(17) 的第3和第5式可认为满足,干扰对齐可行的条件可简化为
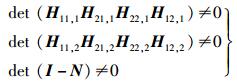
|
(18) |
下面运用注水原理,针对增益大的链路分配较多的发射功率,同时针对增益小的链路分配较少的发射功率,可进一步提高传输容量.
hklji表示发端(源端或中继端)l的第i个符号到收端(中继或目的端)k的第j个符号的等效传输
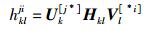
|
(19) |
其中:U[j*]k为收端k的处理矩阵的第j行,Hkl为发端l到收端k的传输矩阵,V[*i]l为发端l的预编码处理矩阵的第i列.第1大跳网络中hkl, 1ji=U[j*]rkHkl, 1V[*i]sl,第2大跳网络中hkl, 2ji=U[j*]dkHkl, 2V[*i]rl.
在收端k接收到的第j个符号中,来自发端k的其他符号的干扰为
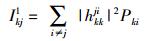
|
(20) |
在收端k的第j个符号中,来自发端l(发端k以外的其他所有发端)的和干扰为
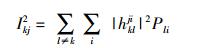
|
(21) |
收端k的第j个符号中总的干扰由以上2部分组成
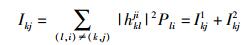
|
(22) |
传输容量为功率的函数,对功率分配进行优化可提高传输容量,则功率分配的优化问题为
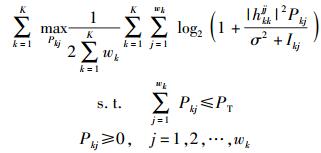
|
(23) |
其中:k为用户对数量,wk为用户k发送向量的符号数,PT为总功率.式(23) 为带约束条件的优化问题,可运用拉格朗日(Lagrangian)乘数法进行求取.构造函数
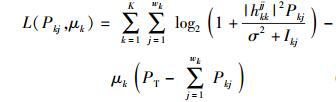
|
(24) |
求L(Pkj, μk)对Pkj的一阶偏导数,令它等于0,并与附加条件联立
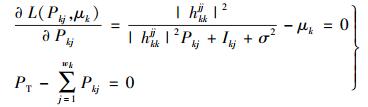
|
(25) |
且由式(25) 转换成如下关系
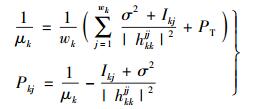
|
(26) |
再考虑到由于单个子信道分配的传输功率必须大于等于0,于是有
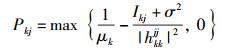
|
(27) |
由于优化的变量有2m-1个,无法一次获得使容量最大化的所有最优的Pkj值,采用迭代的方法来求解优化问题.其中Pkj(r),Ikj(q),μkj(r)表示第q次迭代计算的值.
1) 由式(25) 的第2式初始化Pkj(0)=PT/wk,迭代次数初始化为q=1;
2) 根据式(22) 计算Ikj(q),由式(26) 的第1式获得的优化值μk(q),代入式(26) 的第2式求得Pkj(q);
3) 功率分配差值|Pkj(q)-Pkj(q-1)| < η(η越小,算法精度越高)迭代结束,否则回到第2) 步进行第q+1次迭代.
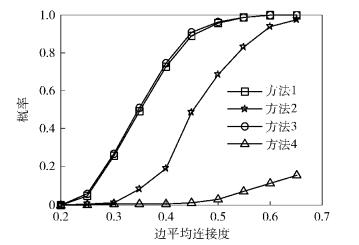
4 仿真结果4.1 干扰对齐可行性分析采用与均匀随机数比较法、概率排序法、赌轮法分别生成边数为p×n(n-1)/2的网络及边数随机生成的与均匀随机数比较法(即生成的网络边的数目不要求为p×n(n-1)/2)4种方法生成中间网络进行干扰对齐及解码可行性的仿真.其中,p为点与点之间边的平均连接度,即网络2点之间可通信的平均概率(0≤p≤1),n为每一大跳网络中的节点个数,且每个大跳内部节点数相同.以上4种方法分别对应仿真图中的方法1、方法2、方法3、方法4.
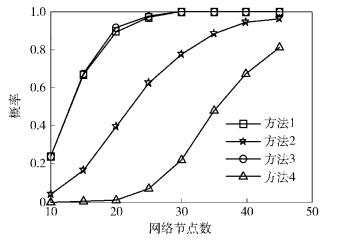
图 2表示无任何约束条件时,干扰对齐可行概率随网络平均连接度p之间的关系,图 3表示干扰对齐可行概率随网络节点个数n之间的关系,由2图可知,在无约束条件下,干扰对齐及解码可行性随着p、n的增大而提高.且在相同的p和n的情况下,由于生成各个网络的平均聚类系数不同,聚类系数值反映图形中节点聚集程度,若聚类系数值越大发端与收端之间存在的链路越多,则满足约束条件概率更大,网络干扰对齐可行性越高.
|
图 2 n=15,p变化时干扰对齐可行概率仿真 |
|
图 3 p=0.4,n变化时干扰对齐可行概率仿真 |
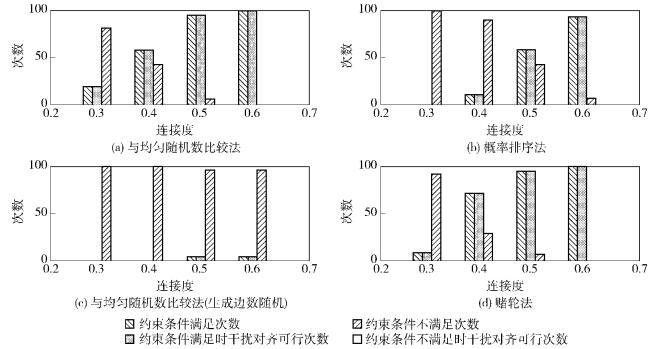
图 4表示在n=15时,以上4种网络在满足简化约束条件的前提下,干扰对齐可行的次数,及不满足约束条件的情况下,干扰对齐可行次数(运行100次),由图 4可知,在相同平均连接度p情况下,只要满足简化约束条件,干扰对齐皆可行,但只要不满足约束条件,干扰对齐就不可行.由此得出,系统模型中,只要式(18) 中的约束条件满足,网络干扰对齐及解码可行.
|
图 4 简化约束条件次数与干扰对齐可行次数对比 |
源端发送向量大小为ws1=4, ws2=3,中继端发送向量大小为wr1=4, wr2=3,在源端,中继端的每个用户总功率分别为相同的PT,噪声功率σ2=0.1,η=10-6,两大跳网络分别求得容量再平均.
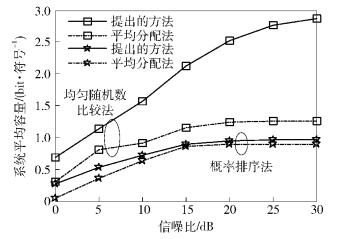
图 5表示在用均匀随机数比较法和概率排序法生成的网络中,网络干扰对齐可行后,源端到中继端网络和中继端到目的端网络的系统平均容量随信噪比的变化图.与所有源端功率与中继端功率平均分配的情况进行对比,发现提出的功率分配方法优于功率平均分配的方法.正如预期的那样,容量随着发送总功率的提高而增加.
|
图 5 系统平均容量 |
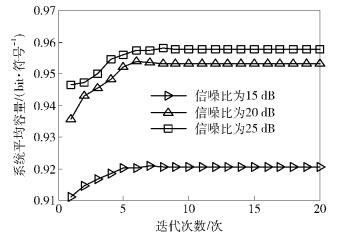
图 6表示平均容量随迭代次数变化的仿真结果.从图 6中可知,在迭代5~10次后,系统容量即收敛.可见提出的算法能成功收敛,且收敛速度较快.
|
图 6 系统平均容量随迭代次数的变化曲线 |
在含有2个中继的情况下,研究了2单播网络源端的预编码、中继端的解码与编码转发、目的端的解码处理方案.运用干扰对齐和网络编码方法,详细分析了网络干扰对齐可行所需的约束条件,并在中继端采用了与源端不同的预编码方法,使目的端能成功解码出源端发送的信号,降低了解码复杂度,同时约束条件也得到了简化.在干扰对齐可行的情况下,对源端和中继端的功率进行了优化分配.相比较平均功率分配,优化后系统的平均容量得到了明显提升.
| [1] | Ramakrishnan A, Das A, Maleki H, et al. Network coding for three unicast sessions: interference alignment approaches[C]//IEEE 48th Annual Allerton Conference on Communication, Control, and Computing. Allerton: IEEE Press, 2010: 1054-1061. |
| [2] | Ganesan A, Bavirisetti T D, Rajan B S. On the feasibility of network alignment for three-source three-destination multiple unicast networks with delays[J].IEEE Global Communications Conference (GLOBECOM), 2012, 3(7): 2274–2279. |
| [3] | Meng Chun, Das A K, Ramakrishnan A. Precoding-based network alignment for three unicast sessions[J].IEEE Transactions on Information Theory, 2015, 61(1): 426–451. doi: 10.1109/TIT.2014.2368556 |
| [4] |
王静, 刘景美, 刘向阳, 等. 基于网络编码的多播网络码字构造[J]. 北京邮电大学学报, 2008, 31(4): 98–101.
Wang Jing, Liu Jingmei, Liu Xiangyang, et al. Construction of codes in multicast network based on network coding[J].Journal of Beijing University of Posts and Telecommunications, 2008, 31(4): 98–101. |
| [5] | Xu Shengfeng, Zhu Gang, Sun Qian, et al. Joint interference alignment and power allocation in MIMO interference network[C]//IEEE 9th International Wireless Communications and Mobile Computing Conference(IWCMC). Sardinia: IEEE Press, 2013: 1258-1262. |
| [6] | Gou Tiangao, Wang Chenwei, Jafar S A. Aligned interference neutralization and the degrees of freedom of the 2×2×2 interference channel with interfering relays[C]//IEEE 49th Annual Allerton Conference on Communication, Control, and Computing (Allerton). Monticello: IEEE Press, 2011: 1041-1047. |


