为了提高多中继系统下俩源节点进行数据交换时的性能, 提出了自适应机会转发策略.在该策略中, 根据2个源节点反馈控制帧的情况, 从直接传输、直接重传、单向机会中继传输和双向机会中继传输4种传输模式中选择最优的传输模式.在只有1个源节点能解码时, 采用源节点重传和单向机会中继竞争的方式.由于该策略能自适应地选择最优的传输模式, 因此相比较其他转发策略, 可以较大地降低系统数据交换的复杂度, 提高系统的中断性能和频谱效率.最后, 通过理论分析和数值仿真验证了该策略的优越性.
In order to improve the performance of the multi-relay system in the case that two sources exchange information with each other, a self-adaptive opportunistic-and-forward scheme is proposed. Based on the feedback transmitted by these two sources, the optimal transmission mode is selected from these four ways: direct transmission, direct retransmission, one-way opportunistic relaying transmission and two-way opportunistic relaying transmission in the proposed scheme. When only one source decoded the received signal correctly, a competition between the source retransmission and one-way opportunistic relaying is adopted. Due to the optimum transmission mode being selected adaptively, so compared to other transmission methods, this proposed scheme can reduce transmission complexity greatly and improve outage performance and spectral efficiency. At last, the superiority of the proposed scheme is verified by theoretical analysis and numerical simulations.
中继选择技术是协同通信研究中的一项关键技术.在近十几年中,该技术受到了广泛的关注.最初的中继选择主要是针对传统的单向中继选择提出的[1-3].为了进一步提高俩源节点在利用中继进行数据交换时的传输效率,提出了双向中继传输策略[4],又称为物理层网络编码.大多数情况下,对于研究放大转发[5-6]和解码转发[7-9]协议下的双向中继选择技术所采用的系统模型,通常假设俩源节点之间不能直接通信.但在实际场景中,俩源节点存在能直接通信的可能.若在直接传输能成功时还采用中继通信,必然会降低数据传输效率,增加系统的复杂度等.通常情况下,俩源节点之间能直接传输就采用直接通信模式,能只利用单向中继传输就尽可能地避免采用双向中继传输所导致的数据处理复杂度.这样就需要一种方法,使中继能根据俩源节点的解码情况来判断是否参与协同通信,是采用单向传输还是双向传输.至今,对该问题的研究较少.为使节点之间的协作更加智能,在俩源节点进行数据交换的模型中,笔者引入反馈机制,提出了一种自适应的机会转发策略.在该策略中,通过俩源节点分时反馈的ACK/NACK帧来自适应选择传输方式.
1 系统模型俩源节点数据交换系统模型是由2个源节点s1,s2和N个中继组成.其中,每个中继用k(k=1, 2, …, N)表示.该模型中的所有节点都配置单根天线,并采用半双工模式,即不能同时收发数据.每个节点都拥有1个定时器.在该模型中,假设各信道相互独立,且为不同分布的循环对称的复高斯随机变量,节点i到节点j的信道参数ij的均值为0,方差为σij2.所有信道满足可逆,即从收发双方看同一信道状态都是对等的,此时满足σij2=σji2.且信道在每组数据传输时间内保持不变,即该信道为准静态信道.进一步假设每个节点发送数据的平均功率为Eξ(ξ∈{s1, s2, 1, 2, …, N}),每条链路接收到的噪声均为加性高斯白噪声,满足均值为0,方差为N0.令γij=Ei|ij|2/N0,相应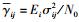
在该模型中,要完成2个源节点之间的数据交换,存在多种通信方式.在2个源节点之间的信道较好的条件下,如果采用传统的4阶段传输或采用3阶段的网络编码传输,会降低系统的传输效率.虽然采用物理层网络编码下的2阶段传输,能较大地提高系统数据交换的效率,但在存在直传路径的实际环境中,相比较传统的4阶段传输,该方法的中断性能较差,而且若在能直接传输成功时刻意地采用该传输策略,只会增加系统的复杂度和不必要的功率消耗.为兼具4阶段传输的高中断性能和2阶段传输的高传输效率等优势,下面给出一种自适应的机会转发策略.
2 自适应机会转发策略在自适应机会转发系统模型中,为了能充分利用所有信道资源,在直传信道较好时,需要直接进行数据交换,因此需要采用2个源节点分时发送数据.这样,在第1个时隙,s1首先广播发送数据x1,此时所有中继节点及s2都接收数据.在第2个时隙,s2广播发送数据x2,所有中继节点和s1接收到数据.在s1和s2发送完数据后,2个源节点根据解码情况分时反馈解码结果,若能正确解码反馈ACK帧,不能正确解码反馈NACK帧.根据2个源节点各自反馈控制帧可知,在前2个时隙,s1和s2的解码状态存在如下几种情况:
① s1和s2都能正确解码,此时s1和s2都反馈ACK帧;
② si能正确解码,而sj不能正确解码,此时si和sj分别反馈ACK帧和NACK帧(若i=1时,j=2;若i=2时,j=1),如图 1所示;
|
图 1 源节点sj不能够正确解码时的传输示意图 |
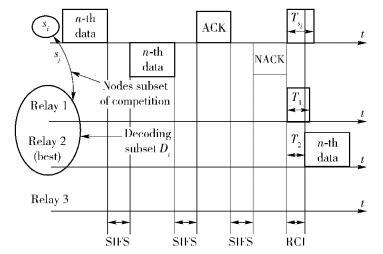
③ s1和s2都不能正确解码,此时s1和s2都反馈NACK帧,如图 2所示.
|
图 2 俩源节点都不能够正确解码时的传输示意图 |
系统根据上述反馈状态,选择最佳的转发方式.
1) 在情况① 时,各中继保持静默,而s1和s2在下个时隙发送下个数据,此时采用直接传输方式.
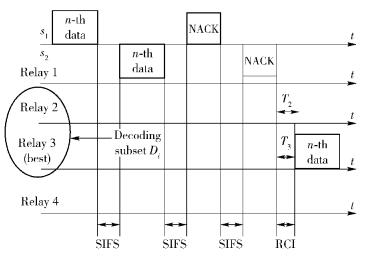
2) 在情况② 时,由于只有sj不能正确解码,因此只需要转发si发送的数据.传统的处理方式可以采用si重传或在有效中继集合中选择最优的中继转发.其中,有效中继集合是指能正确解码si发送的数据的中继集合,满足
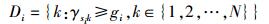
|
(1) |
其中:gi为判断接收到si发送的数据能否正确解码的信噪比(SNR)门限.为了选择最佳的转发模式,采用si和所有有效中继k∈Di竞争的模式.竞争过程如图 1所示.可以简单描述为:在si和所有中继接收到sj反馈的NACK帧后,所有中继立即检查自身是否能正确解码si所发的数据. si和Di中的中继节点利用接收到sj反馈的NACK帧估计出自身到sj之间的信道参数hζsj,然后利用该参数值,设定节点ζ的定时器初值,满足Tζ=λ/(Eζ|hζsj|2)(其中ζ∈Di∪{si},λ为一预设常数).立即启动定时器归零,展开节点之间的竞争,竞争时间即为最先归零节点的等待时间.在各竞争节点计时过程中,持续探测信道,若一旦发现其他节点开始发送数据,而自身定时器还没有归零,则认为自身竞争失败,退出竞争;若该节点一直到定时器归零还没有发现其他节点发送数据,则认为自身竞争成功,即为最佳转发节点,该节点立即开始转发数据.由此可知,最优转发模式节点的选择需要满足
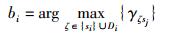
|
(2) |
3) 在情况③ 时,由于源节点s1和s2都不能正确解码,选择的中继需要同时转发源节点s1和s2发送的数据,因此最优中继的选择必须从能同时正确解码s1和s2发送数据的中继集合中选择,该集合满足
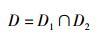
|
(3) |
因此,所有中继在接收到s1和s2发送的NACK帧时,立即检查自身是否能同时解码s1和s2发送的数据,集合D中的中继k根据接收到俩源节点反馈的NACK帧,估计出相应的2条信道的参数值hks1和hks2,利用该参数设定中继k定时器初始值,满足Tk=λ/min{αkEk|hks1|2, βkEk|hks2|2}(其中:k∈D,αk,βk的取值与中继接收到2个源节点数据编码转发的方式有关,若中继采用比特级异或转发机制,则αk=βk=1;若采用叠加码转发机制,则满足αk+βk=1,0<αk, βk<1).立即启动自身定时器展开中继间的竞争,竞争过程如图 2所示.最先归零的中继即为最优中继.最优中继可以表示为
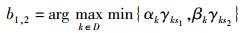
|
(4) |
需要说明的是,在上述3种情况下的节点竞争时间RCI不一定相同.
3 中断性能分析3.1 精确中断性能分析在自适应机会转发系统模型中,完成1次正确传输,需要2个源节点都能正确解码,因此只要一方不能解码,就存在中断.
1) 单向传输的中断性能分析
在情况② 时,N个中继中存在ξ个有效中继的集合有N!/[(N-ξ)!ξ!]种可能.用Dil(ξ)表示第l个能正确解码si发送数据的中继集合,那么Dil(ξ)发生的概率为
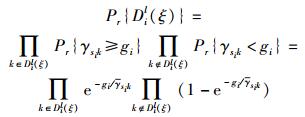
|
(5) |
其中:
在ξ=0时,定义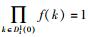
在ξ=N时,定义
在ξ=0时,由于不存在正确解码中继,只能采用直接重传模式,此时的中断概率为
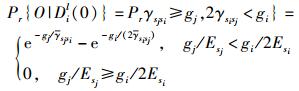
|
(6) |
其中O表示中断.
在ξ>0时,令

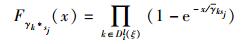
|
(7) |
由于在γsisj≥γk*sj时,采用直接重传方式,而在γsisj < γk*sj时,采用中继k*转发模式.利用式(7) 可以得到

|
(8) |
由式(5)、式(6) 和式(8) 可得,在情况② 时的中断概率为
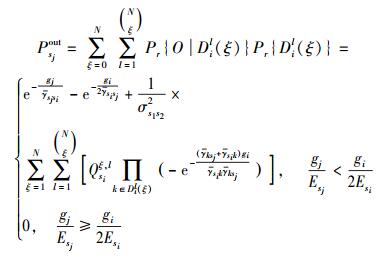
|
(9) |
其中
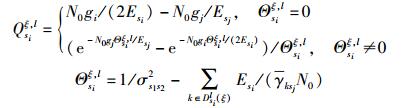
|
2) 双向传输的中断性能分析
在情况③ 时,令中继k能正确解码s1和s2发送的数据的事件满足
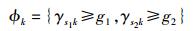
|
(10) |
解码中继k发送的数据,能被s1和s2正确解码的事件表示为
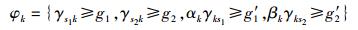
|
(11) |
其中:g′1和g′2分别表示中继k发送数据到s1和s2时,对应判断能否正确解码的SNR门限.
在解码中继个数为ξ时,在第l个解码集合Dl(ξ)中,系统的中断概率为
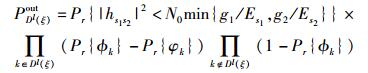
|
(12) |
由式(10)~(12) 可得,在情况③ 时,系统的中断概率为
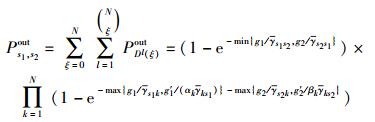
|
(13) |
把式(9) 和式(13) 的结果代入式(14),即可得到该系统总的精确中断概率为
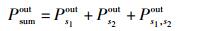
|
(14) |
利用在x→0时满足ex≈1+x+x2/2可知,在高SNR时,式(9) 和式(13) 的结果可进一步表示为
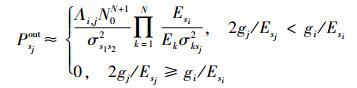
|
(15) |
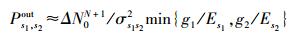
|
(16) |
其中: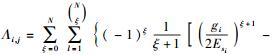
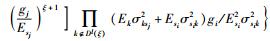
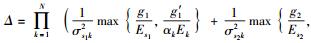

令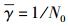
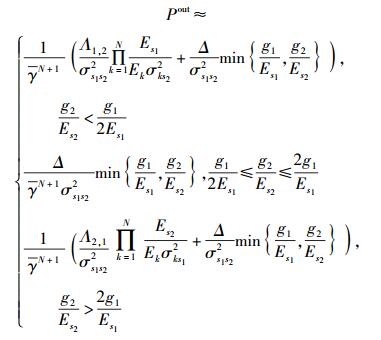
|
(17) |
从式(17) 可以看出,该策略的最大分集阶数为N+1.
4 性能仿真分析为了简化仿真过程,采用相同的信噪比门限g1=g2=g′1=g′2=22R-1,R=2 bit·s-1·Hz-1,N=3.所有中继到同一个源节点的信道具有相同的统计特性,且每个中继的发射功率相同.
图 3给出了不同情况下,自适应机会转发策略的中断概率的理论分析结果、高SNR时的近似结果及蒙特卡罗仿真随SNR变化的仿真对比.从图 3可以看出,理论结果和蒙特卡罗仿真很好地重合,验证了理论分析的正确性,且在高SNR范围时,中断概率近似结果很好地逼近精确结果.

|
图 3 中断概率随SNR变化的仿真对比 |
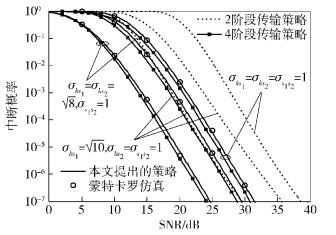
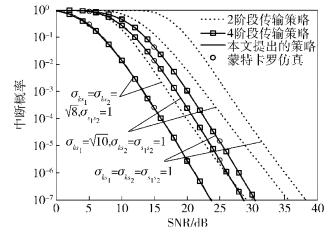
图 4和图 5分别给出了Es1=Es2=Ek时和Es1/3=Es2=Ek时,该策略与物理层网络编码下的2阶段传输及传统的4阶段传输的中断概率性能仿真对比.从图 4可以看出,在等功率的条件下,自适应机会转发策略要达到与传统的4阶段传输相同的中断性能,只需要增加不到1 dB的SNR性能,但在传输效率方面相比,至少提高50%.相比物理层网络编码下的2阶段传输策略,虽然传输效率存在降低50%的可能,但在达到相同的中断性能,在σks1=σks2=8,σs1s2=1时,至少有5 dB的SNR性能提高,而在σks1=σks2=σs1s2=1时,约有7 dB的SNR性能提高.从图 5可以看出,在俩源节点不等功率的条件下,自适应机会转发策略的中断性能基本与传统4阶段传输的相同,而相比较物理层网络编码下的2阶段传输的中断性能,在σks1=σks2=8,σs1s2=1时,同样大约有5 dB的SNR性能提高,而在σks1=σks2=σs1s2=1时,同样大约有7 dB的SNR性能提高.
|
图 4 等功率时不同策略的中断概率随SNR变化的仿真对比 |
|
图 5 不等功率时不同策略的中断概率随SNR变化的仿真对比 |
结合MAC层协议,提出了自适应机会转发策略,该策略根据俩源节点反馈控制帧不同的情况而自动选择不同的转发模式.可以降低系统转发方式的复杂度,提高系统的中断性能和传输效率.由于该策略实施简单有效,并且可以非常方便地运用到现有的无线网络中,能够有效地在实际环境中得到应用.
| [1] | Bletsas A, Khisti A, Reed D P, et al. A simple cooperative diversity method based on network path selection[J].IEEE J Select Areas Commun, 2006, 24(3): 659–672. doi: 10.1109/JSAC.2005.862417 |
| [2] | Bletsas A, Shin H, Win M Z. Cooperative communications with outage-optimal opportunistic relaying[J].IEEE Trans Wireless Commun, 2007, 6(9): 3450–3460. doi: 10.1109/TWC.2007.06020050 |
| [3] | Wang Heng, Yang Shizhong, Lin Jinzhao. A distributed selection cooperation protocol with feedback and its DMT in Nakagami-m fading channels[J].IEEE Commun Lett, 2009, 13(11): 844–846. doi: 10.1109/LCOMM.2009.091519 |
| [4] | Rankov B, Wittneben A. Spectral efficient protocols for half-duplex fading relay channels[J].IEEE J Select Areas Commun, 2007, 25(2): 379–386. doi: 10.1109/JSAC.2007.070213 |
| [5] | Li Enyu, Yang Shizhong. Simple relay selection criterion for general two-way opportunistic relaying networks[J].IET Electron Lett, 2012, 48(14): 881–882. doi: 10.1049/el.2012.1296 |
| [6] | Salhab A M, Zummo S A. A low-complexity relay selection scheme based on switch-and-examine diversity combining for AF relay systems[J].IET Commun, 2013, 7(9): 848–859. doi: 10.1049/iet-com.2012.0659 |
| [7] | Ioannis K. Relay selection for two-way relay channels with MABC DF: a diversity perspective[J].IEEE Trans Veh Technol, 2010, 59(9): 4377–4387. doi: 10.1109/TVT.2010.2070087 |
| [8] | Zhi Hui, Yang Longxiang, Zhu Hongbo. Outage probability and ergodic capacity analysis for two-way relaying system with different relay selection protocols[J].Wireless Pers Commun, 2013, 72(4): 2281–2294. doi: 10.1007/s11277-013-1149-1 |
| [9] | Zou Yulong, Wang Xianbin, Shen Weiming. Optimal relay selection for physical-layer security in cooperative wireless networks[J].IEEE J Select Areas Commun, 2013, 31(10): 2099–2111. doi: 10.1109/JSAC.2013.131011 |


