2. 北京邮电大学 经济管理学院, 北京 100876;
3. 北京航空航天大学 经济管理学院, 北京 100191
为有效对功能型布局制造系统进行调度, 构建批量零件的加工与搬运时间模型, 设计考虑了搬运车辆总投入数量、搬运次数均衡程度、搬运车辆总空载转移时间等指标的基于单运输工序的搬运车辆协作调度算法.研究结果表明, 本算法可为同类型批量零件制定精确的生产与搬运作业计划, 生成用于支撑搬运车辆调度算法所需的时间信息; 可对搬运车辆进行准确调度, 特别是与其他搬运车辆调度算法相比, 在搬运车辆总投入数量、搬运次数均衡程度等方面具有明显优势.
2. School of Economics and Management, Beijing University of Posts and Telecommunications, Beijing 100876, China;
3. School of Economics and Management, Beihang University, Beijing 100191, China
Aiming at making an effective schedule for the functional layout manufacturing system, the processing and handling time models were established. Meanwhile, taking the total number of the handling vehicles, the equilibrium degree of handling times and the total no-load transfer time of the handling vehicles into consideration, a new handling vehicle collaboration scheduling algorithm based on the single transport process was designed. It is shown that the study in this article could make the production schedule and handling plan more accurately for the same type of batch parts, generate useful time information required by the designed handling vehicle collaboration scheduling algorithm, and schedule the handling vehicles more precisely. Especially compared with other transport vehicles' scheduling algorithms, there are obvious advantages in aspects of the total number of the handling vehicles and the equilibrium degree of handling times.
目前,订单驱动型制造方式已成为主要生产模式.许多订单驱动型制造企业普遍采用功能型布局制造系统.在为该制造系统批量零件制定生产作业计划时必须考虑运输工序的搬运时间,因此会涉及搬运车辆的调度问题.生产周期是制定生产作业计划的基础数据.关于生产周期(最大完工时间)理论和实践的许多研究成果[1-3]都只考虑了工艺工序的加工时间.因此,计算出的生产周期比批量零件的真实生产时间小.依据不准确的数据制定生产作业计划,必然会影响计划的可行性.在考虑运输工序的搬运时间方面,贾国柱等[4]给出批量零件的生产周期公式,并设计局部优化算法调度搬运车辆;孔继利等[5]给出人工作业系统批量零件的生产周期模型,并设计全局优化算法调度搬运车辆;孔继利等[6]给出平行移动方式中批量零件的加工与搬运时间模型,并设计互助组优化算法调度搬运车辆.以上关于搬运车辆调度算法的研究都只考虑单一优化目标.
在考虑搬运时间的基础上,对一类订单驱动型功能布局制造系统的调度问题进行研究.构建批量零件的加工时间模型和搬运时间模型,并设计基于单运输工序的搬运车辆协作调度算法.
1 假设条件及参数说明1.1 模型假设条件本模型除了基于相关研究文献[4, 6]给定的假设条件外,还特别关注如下假设条件:
1) 工艺工序的加工制造设备和运输工序的搬运车辆在制造系统运行过程中不发生故障;
2) 零件装载至搬运车辆上的时间忽略不计;
3) 制造系统的生产效率只由加工制造设备的生产效率和搬运车辆的搬运效率决定;
4) 从第i运输工序向第(i+k)道运输工序转移时,搬运车辆的转移时间为tiT+ti+1T+…+t(i+k)-1T;
5) 运输批量不固定,在不影响生产周期的前提下,按“搬运次数最少”原则安排零件的运输批量.
1.2 参数及变量说明1) m为工艺工序总数(m≥2).
2) n为零件的加工批量(n≥2).
3) tiP为零件在第i道工艺工序中的单件加工时间(i=1, 2, …, m).
4) tiT为零件在第i道运输工序中的搬运时间(i=1, 2, …, m-1).
5) t(i, j)BpP、t(i, j)EpP和Tp分别为平行移动方式中第i道工艺工序中第j个零件开始加工时间、结束加工时间和批量零件的生产周期.
6) t(i, j)BpT′、t(i, j)EpT′分别为平行移动方式中第i道运输工序中第j个零件未优化时的开始搬运时间、结束搬运时间.
7) t(i, j)Bp-sP、t(i, j)Ep-sP和Tp-s分别为平行顺序移动方式中第i道工艺工序中第j个零件开始加工时间、结束加工时间和批量零件的生产周期.
8) t(i, j)Bp-sT′、t(i, j)Ep-sT′分别为平行顺序移动方式中第i道运输工序中第j个零件未优化时的开始搬运时间、结束搬运时间.
9) t(i, j)EBT、t(i, j)LBT分别为某移动方式中已经优化后的第i道运输工序中第j次搬运的最早开始搬运时间、最晚开始搬运时间.
10) tBH(u, vu, i)、tEH(u, vu, i)分别为某移动方式中第i道运输工序中第u台搬运车辆第vu次搬运的开始搬运时间、结束搬运时间.
11) Tiloadsum、Tino-loadsum和T(i→i′)sum分别为某移动方式中搬运车辆在第i道运输工序中的有载搬运时间、空载转移时间和搬运车辆在第i与i′道运输工序之间的空载转移时间.
12) ta(u′, vu′, i)为某种移动方式中第i道运输工序中第u′台搬运车辆在vu′次搬运中最早可用于搬运的时间.
13) TP={tiP|i=1, 2, …, m}为工艺工序的单件加工时间集合.
14) TT={tiT|i=1, 2, …, m-1}为运输工序的搬运时间集合.
15) H为所有搬运车辆搬运次数的均值.
16) g为搬运车辆的总数量.
2 加工与搬运时间模型构建2.1 平行移动的加工与搬运时间模型1) 第i道工艺工序中第j个零件开始加工和结束加工时间模型
① 开始加工时间模型
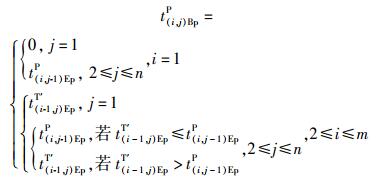
|
(1) |
② 结束加工时间模型
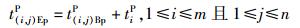
|
(2) |
2) 搬运时间未优化时,第i道运输工序中第j个零件开始搬运和结束搬运时间模型
① 未优化时的开始搬运时间模型
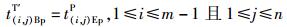
|
(3) |
② 未优化时的结束搬运时间模型
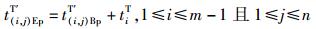
|
(4) |
3) 平行移动方式的生产周期
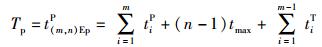
|
(5) |
1) 第1道工艺工序中第j个零件开始加工和结束加工时间模型
① 开始加工时间模型

|
(6) |
② 结束加工时间模型
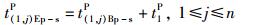
|
(7) |
2) 搬运时间未优化时,第i道运输工序中第j个零件开始搬运和结束搬运时间模型
① 未优化时的开始搬运时间模型
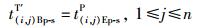
|
(8) |
② 未优化时的结束搬运时间模型

|
(9) |
3) 第i(2≤i≤m)道工艺工序中第j个零件开始加工和结束加工的时间模型
① 当ti-1P≤tiP时
a.开始加工时间模型
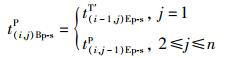
|
(10) |
b.结束加工时间模型
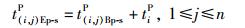
|
(11) |
② 当ti-1P>tiP时
a.结束加工时间模型
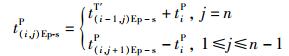
|
(12) |
b.开始加工时间模型
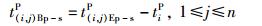
|
(13) |
4) 平行顺序移动方式的生产周期
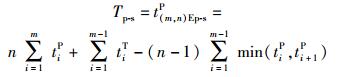
|
(14) |
批量零件在平行移动方式和平行顺序移动方式中的搬运时间优化模型的求解流程可参阅文献[5]中的循环体(1).
3 搬运车辆调度算法的分析与设计搬运车辆调度算法的目标是使全部运输工序所需搬运车辆总投入数量小、搬运车辆搬运次数均衡程度好、搬运车辆总空载移动时间小等.可把某种移动方式(平行或平行顺序)中的开始搬运时间、运输工序的搬运时间等数据作为输入,构建基于单运输工序的搬运车辆协作调度算法,求解过程如下.
1) 单运输工序中的搬运车辆调度算法
① 从第i道运输工序未完成的搬运任务中找出最小的最早开始搬运时间,并记录最早开始搬运时间t(i, j)EBT和最晚开始搬运时间t(i, j)LBT.
② 若某次搬运是第i道运输工序中的第1次搬运,则需要新投入一台搬运车辆,令搬运车辆的编号u=1,搬运车辆u的第vu次搬运vu=1,该台搬运车辆开始搬运时间为tBH(u, vu, i)=t(i, j)EBT,该台搬运车辆结束搬运时间为tEH(u, vu, i)=tBH(u, vu, i)+tiT,令vu=vu+1,Tiloadsum=tiT,Tino-loadsum=0,将第i道运输工序中的第j次搬运任务设定为已完成的搬运任务;否则,判断已有的哪台搬运车辆可用于本次搬运任务,规则如下:a.计算已投入的搬运车辆最早可用于搬运的时间为ta(u′, vu′, i)=tEH(u′, vu′-1, i)+tiT;b.若ta(u′, vu′, i)>t(i, j)LBT时,需要新投入1台搬运车辆,令u=u+1,vu=1,tBH(u, vu, i)=t(i, j)EBT,tEH(u, vu, i)=tBH(u, vu, i)+tiT,令vu=vu+1,Tiloadsum=Tiloadsum+tiT,Tino-loadsum=Tino-loadsum+0,将第i道运输工序中的第j次搬运任务设定为已完成的搬运任务;否则,选择ta(u′, vu′, i)最小的搬运车辆完成本次搬运任务;用已选中的第u′台搬运车辆完成第vu′次搬运任务的规则如下:a.若ta(u′, vu′, i)≤t(i, j)EBT时,则tBH(u′, vu′, i)=t(i, j)EBT,tEH(u′, vu′, i)=tBH(u′, vu′, i)+tiT,令vu′=vu′+1,Tiloadsum=Tiloadsum+tiT,Tino-loadsum=Tino-loadsum+tiT,将第i道运输工序中的第j次搬运任务设定为已完成的搬运任务;b.若t(i, j)EBT < ta(u′, vu′, i)≤t(i, j)LBT时,则tBH(u′, vu′, i)=ta(u′, vu′, i),tEH(u′, vu′, i)=tBH(u′, vu′, i)+tiT,令vu′=vu′+1,Tiloadsum=Tiloadsum+tiT,Tino-loadsum=Tino-loadsum+tiT,将第i道运输工序中的第j次搬运任务设定为已完成的搬运任务.
③ 重复步骤① 和②,直到该道运输工序中的所有搬运任务都已完成,令g=u,输出变量g和{v1-1, v2-1, …, vg-1}、
2) 运输工序间的协作调度算法
① 令T(i→i′)sum=0.
② 按运输工序编号升序方式进行检查,若tEH(u, vu-1, i)+t(i→i′)T≤t(u′, v′, i′)BH(vu≥2且i′>i),且若第i道运输工序中投入的第u台搬运车辆取代了第i′道运输工序中投入的第u′台搬运车辆,不影响各自运输工序中搬运任务的完成且不需再新增投入到各自运输工序中的搬运车辆,则可考虑用第i道运输工序中投入的第u台搬运车辆取代第i′道运输工序中投入的第u′台搬运车辆;若可取代方案的数量≥2,则选择搬运车辆搬运次数均衡程度优的取代方案,若搬运车辆搬运次数均衡程度相同,则选择使搬运车辆总空载转移时间小的取代方案.若已确定用第i道运输工序中投入的第u台搬运车辆取代第i′道运输工序中投入的第u′台搬运车辆,则令T(i→i′)sum=T(i→i′)sum+t(i→i′).否则,不可取代.
③ 重复步骤②,至检查完第(m-2) 道运输工序为止;之后,输出搬运设备总数量和T(i→i′)sum.
4 数值实例与结果分析4.1 数值实例以文献[4]中的数据为例,对一类功能型布局设备工序制造系统的调度情况进行分析.其中,该批零件的加工批量n=5,工艺工序的单件加工时间集合TP={10, 25, 8, 50, 38, 30},运输工序的搬运时间集合TT={5, 12, 7, 10, 13},时间单位都为min.
4.2 批量零件的生产作业计划与搬运计划在该数据实例中,批量零件以平行顺序移动方式完成制造,则各道工艺工序中各个零件开始加工时间矩阵TBP和结束加工时间矩阵TEP、各道运输工序各次搬运零件个数矩阵NT、第1道和第5道运输工序各次搬运时间矩阵T1h和T5h的详细信息如下所示.

|
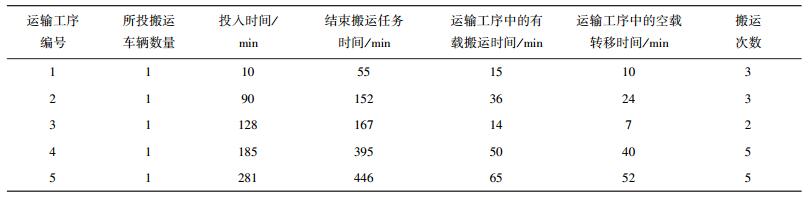
1) 单运输工序中的搬运车辆调度结果
利用单运输工序中的搬运车辆调度算法,可得出搬运车辆调度结果,如表 1所示.
|
|
表 1 单运输工序中的搬运车辆调度结果 |
2) 运输工序间的协作调度结果
① 第1道运输工序中的第1台搬运车辆可取代第2道运输工序中的第1台搬运车辆,其在运输工序1和2之间的空载转移时间为0 min.
② 第2道运输工序中的第1台搬运车辆可取代第4道运输工序中的第1台搬运车辆,其在运输工序2和4之间的空载转移时间为7 min.
③ 第3道运输工序中的第1台搬运车辆可取代第5道运输工序中的第1台搬运车辆,其在运输工序3和5之间的空载转移时间为10 min.
3) 搬运车辆的最终调度结果
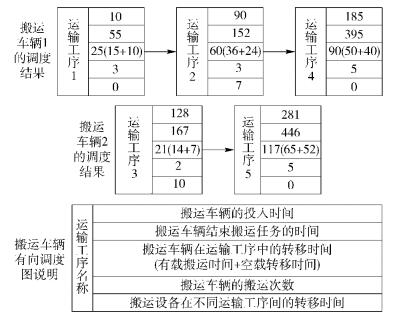
基于单运输工序的搬运车辆协作调度算法的调度结果可表示为搬运车辆有向调度图,如图 1所示.
|
图 1 搬运车辆有向调度图 |
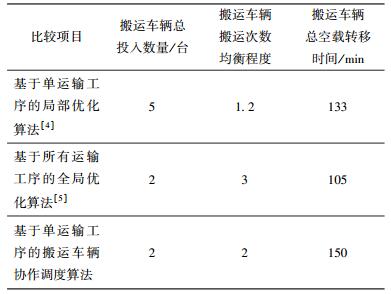
将设计的基于单运输工序的搬运车辆协作调度算法与文献[4]和文献[5]中设计的算法的计算结果进行比较. 3类搬运车辆调度算法所得关键绩效指标(KPI,key performance indicator)结果如表 2所示.
|
|
表 2 3类搬运车辆调度算法所得KPI结果 |
其中,规定搬运车辆搬运次数的均衡程度指标用Hed表示,其计算公式为

|
(15) |
3类搬运车辆调度算法结果的对比分析如下.
1) 搬运车辆总投入数量指标:基于单运输工序的局部优化算法所需搬运车辆总投入数量最多,基于所有运输工序的全局优化算法和单运输工序的搬运车辆协作调度算法所需搬运车辆总投入数量相等且较少.
2) 搬运车辆搬运次数均衡程度指标:基于单运输工序的局部优化算法所得到的搬运车辆搬运次数均衡程度最小,基于单运输工序的搬运车辆协作调度算法所得到的搬运车辆搬运次数均衡程度居中,基于所有运输工序的全局优化算法所得到的搬运车辆搬运次数均衡程度最大.
3) 搬运车辆总空载转移时间指标:基于所有运输工序的全局优化算法所求得的搬运车辆总空载转移时间最短,基于单运输工序的局部优化算法所求得的搬运车辆总空载转移时间居中,基于单运输工序的搬运车辆协作调度算法所求得的搬运车辆总空载转移时间最长.
以搬运车辆投入的总数量、搬运车辆搬运次数的均衡程度、搬运车辆的总空载转移时间作为第1、第2、第3决策目标,按分层序列法进行多目标决策,则基于单运输工序的搬运车辆协作调度算法可作为进行搬运车辆调度的最优方法.
5 结束语对订单驱动型功能布局制造系统调度问题展开研究,取得如下成果:1) 为在这类制造系统中加工的同类型批量零件建立两类加工与搬运时间模型,利用该模型,生产作业计划人员可在选定某种移动方式后精确地制定批量零件的加工与搬运任务;2) 设计基于单运输工序的搬运车辆协作调度算法,利用该算法,车辆调度人员可对运输工序所需的搬运车辆进行合理调度;3) 本研究中的搬运车辆有向调度图以更加直观、形象的方式给出各类有效信息,可辅助管理人员进行决策.本研究尚存在需要进一步分析的问题:可考虑批量零件装载至搬运车辆时间不忽略的情况,或考虑在第i运输工序与第(i+k)道运输工序之间直接存在搬运路径的情况;也可以设计新搬运车辆调度算法.
| [1] |
宁维巍, 雷毅, 仲华惟, 等. 无等待排列流水车间提前/延期调度问题[J]. 北京邮电大学学报, 2009, 32(6): 72–76.
Ning Weiwei, Lei Yi, Zhong Huawei, et al. Researches on the no-wait permutation flow shop earliness and tardiness scheduling problem[J].Journal of Beijing University of Posts and Telecommunications, 2009, 32(6): 72–76. |
| [2] | Yenisey M M, Yagmahan B. Multi-objective permutation flow shop scheduling problem: literature review, classification and current trends[J].Omega, 2014, 45(2): 119–135. |
| [3] |
曾强, 杨育, 程博, 等. 平顺移动下等量分批FJSP多目标优化研究[J]. 系统仿真学报, 2012, 24(5): 1046–1052.
Zeng Qiang, Yang Yu, Cheng Bo, et al. Research on multi-objective optimization for equal batch splitting FJSP under parallel and sequence shift mode[J].Journal of System Simulation, 2012, 24(5): 1046–1052. |
| [4] |
贾国柱, 孔继利. 考虑运输时间的加工装配型企业批量加工模式系统设计[J]. 工业工程, 2013, 16(2): 104–111.
Jia Guozhu, Kong Jili. System design of batch processing modes in processing-assembly enterprise with transit time considered[J].Industrial Engineering Journal, 2013, 16(2): 104–111. |
| [5] |
孔继利, 贾国柱, 栾世超, 等. 考虑学习率和搬运时间的人工作业系统批量加工模式研究[J]. 系统工程理论与实践, 2013, 33(8): 1965–1974.
Kong Jili, Jia Guozhu, Luan Shichao, et al. Batches processing modes for manual operating system considering learning rate and handling time[J].Systems Engineering-Theory and Practice, 2013, 33(8): 1965–1974. doi: 10.12011/1000-6788(2013)8-1965 |
| [6] |
孔继利, 贾国柱. 考虑搬运时间的多品种、小批量混流制造系统批量加工模式的优化与资源调度[J]. 系统工程理论与实践, 2014, 34(11): 2801–2807.
Kong Jili, Jia Guozhu. Optimization of the batches processing modes and resource scheduling for mixed-model manufacturing system of multi-variety and small-batch considering handling time[J].Systems Engineering-Theory and Practice, 2014, 34(11): 2801–2807. |