根据在线社区中群体的历史行为进行物品(或信息)推荐是当前研究热点之一, 传统推荐算法都面临数据稀疏性问题的挑战.针对传统推荐算法知识表示的局限性进行了研究, 提出了一种基于标签系统的用户行为知识表示法, 把用户在物品上历史行为的统计, 转化为对用户在物品标签上的统计, 从而缓解数据稀疏的情况.为了降低标签维度过高导致的计算复杂性问题, 提出了采用因子分析法, 抽取出潜在重要且稳定的特征因子向量来最终表示用户的历史行为, 并据此度量用户行为在特征因子向量上的相似性.最后采用协同过滤的思想给出了一种新的协同推荐方法.通过在真实数据集上的大量对比实验, 表明该方法在处理具有稀疏性的数据集时, 总是能保持更高且更稳定的推荐准确率.
Item (or information) recommendation is one of hot research topics currently. However the issue of sparseness in dataset challenges all traditional recommendation algorithms. Limitations of knowledge representation in traditional recommendation algorithms were studied. The tag-system-based knowledge to represent information of each user's behavior was proposed. That it the account on user's behavior on items is transferred to an account on a user's behavior on tags. To decrease the computation complexity on high dimensional tag-based datasets, a factor analysis method was taken to extract those most important latent factors to represent users' behaviors. Based on each user's representing vector of latent factors, a new way was given to compute similarities among users. By incorporating this similarity measure, a new collaborative recommendation method with low sensitivity to sparseness was built to meet the need of practical and dynamic datasets. Experiments were carried on real-world datasets to compare the proposed method with other state-of-the-art collaborative filtering and matrix factorization based recommendation methods. It is shown the proposed method can achieve better prediction accuracy while keeps a lower sensitivity to sparseness.
基于用户和项的User-Item评分矩阵模型是推荐系统领域里最为经典和有效的数据模型.众多的现实推荐问题都可以通过转化为User-Item评分矩阵进行建模和处理.然而,由于User和Item的数据规模通常处于一个较大的数量级,而User-Item矩阵中有效的评分数据往往很少(不足5%),这就产生了评分数据集的稀疏性问题[1-2].
针对User-Item矩阵的稀疏性问题,学者们从不同方面进行了研究,提出了一些应对数据稀疏性的方法.在User-Item矩阵外引入其他相关信息来弥补数据稀疏,如利用社会网络[3]、信任网络[4]、矩阵分解[5]、扩散[6]、内部一致[7]、转移相似性[8]等方法发掘用户和物品潜在的关联关系等.这些方法同样存在着一些不足,如涉及的辅助信息太多、推荐算法时间复杂度较高以及处理的数据集往往是静态的等.
标签(tag)是一种对网络资源进行标记、分享及识别的工具,标签信息相对稳定.通过将商品抽象为标签,建立用户对标签的偏爱或兴趣分布,一方面可以了解用户的喜好特征,另一方面可以减弱原始数据集稀疏程度对推荐算法的影响.因子分析方法可以抽取决定性因子,有效降维和除噪.因此笔者提出一种基于标签和因子分析方法的推荐方法.
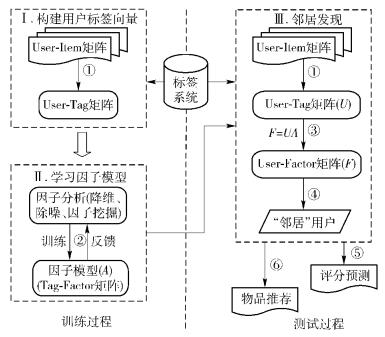
1 推荐算法框架推荐算法框架流程如图 1所示. 图 1中步骤① 表示构建User-Tag矩阵. User-Tag矩阵是一个以用户为行、标签为列的2维矩阵,它由原始的User-Item矩阵变换而来,矩阵中的每一行表示一个用户对所有标签的兴趣分布.步骤② 表示学习因子模型,通过对步骤① 获得的User-Tag矩阵(一个样本)进行因子分析,挖掘出样本中不同兴趣分布背后隐藏的一些潜在因子并建立一种描述潜在因子与原标签关系的因子模型.该因子模型是一个经过数据除噪、降维后的Tag-Factor矩阵. Tag-Factor矩阵以标签为行、因子为列,每一列表示一个因子(Factor)与原始标签(Tag1~Tagm)的线性组合关系.步骤③ 表示利用因子模型Tag-Factor矩阵为训练集中的所有用户建立新的User-Factor向量,这些向量的集合构成User-Factor矩阵.步骤④ 计算不同用户向量之间的相似度.基于获得的目标用户的“邻居”,可以将“邻居”曾经打分较高且目标用户没有评分过的物品对目标用户进行推荐(步骤⑤),也可以定义一个基于目标用户“邻居”的评分预测方法来对目标用户未评分的物品进行评分预测(步骤⑥).式(1) 描述了一种常用的根据目标用户“邻居”预测目标用户未知评分的计算方法.
|
图 1 算法流程 |
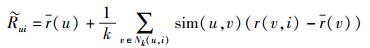
|
(1) |
其中: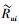
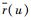
假设某标签系统为某类物品预先定义了p个标签.用户u对物品i有过评分且物品i对应有p个标签中的n个标签,则物品i对应的每个标签将获得关注度1/n.由此用户u对标签t的关注度可以表示为
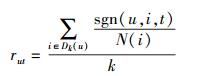
|
(2) |
其中: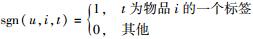
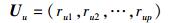
|
(3) |
多个User-Tag向量的集合构成了User-Tag矩阵.
2.2 潜在因子挖掘设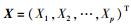
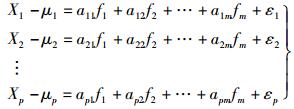
|
(4) |
其中:μ1, μ2, …, μp为随机变量X1, X2,…, Xp的数学期望;f1, f2, …, fm(m < p)为公共因子,ε1, ε2, …, εp为特殊因子,它们都是不可观测的随机变量.式(4) 也可以写成
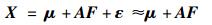
|
(5) |
设X(1), X(2), …, X(n)是一组p维个体组成的样本,其中X(i)=(xi1, xi2, …, xip)T,则样本协方差矩阵的估计量为
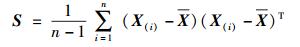
|
(6) |
其中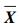
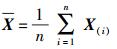
由式(4) 的性质[9]可得
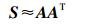
|
(7) |
设样本的协方差阵S的特征值为λ1≥λ2≥…≥λp≥0,相应的单位正交特征向量为l1, l2, …, lp,从而当前m个特征值的总和远大于最后(p-m)个特征值的总和时有
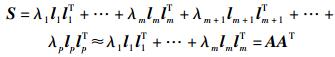
|
(8) |
则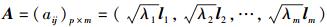
假设数据集的因子模型为A,为User-Item评分矩阵建立的User-Tag矩阵为U,则User-Factor矩阵F可表示为
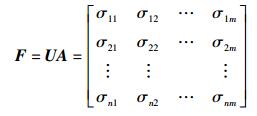
|
(9) |
其中: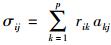
为验证所提出方法在评分预测方面的准确性以及对稀疏数据集的低敏感性,选取了推荐领域MovieLens 1 M(http://www.datatang.com/data/44521)数据集进行实验(注:在其他数据集上得到的实验结果类似,不再重复结果).该数据集包含2000年3 900个匿名用户对6 040部电影的1 000 209个评分(稀疏度为4.2%),标签的种类共有18种,每部电影由1个或多个标签构成.数据集分为2个部分:训练集包含3 000个用户,测试集包含剩余的3 040个用户.训练集用来学习因子模型,然后用训练集获得的因子模型对测试集中的用户进行User-Factor向量生成,并基于生成的User-Factor向量计算用户的Top-N个邻居及利用Top-N邻居对目标用户进行评分预测.为方便起见,下面将提出的方法记为Native方法.
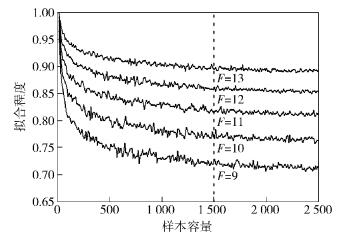
3.1 实验一:因子个数选择在建立因子模型的过程中,为了确定应当从多少个样本用户中抽取多少个因子来建立因子模型,进行了以下实验.实验结果如图 2所示.
|
图 2 拟合程度和样本数量关系 |
图 2中横轴代表从训练集中随机选择的用户数,纵轴表示得到的因子模型对训练集中选择的样本数据的拟合程度,K表示指定的因子个数.从图 2中可知,拟合程度随着样本数的增多而下降,其原因是当因子个数一定时,随着数据量的增大,拟合所有数据的难度随之增加.当样本数增加到1 500个时,因子的拟合程度基本收敛.一般而言,为了防止过拟合,通常选择拟合程度为80%.因此使用的训练样本为从3 000个用户中随机选择1 500个,挖掘的因子个数选定为K=11.
3.2 实验二:准确性评估为了对比Native方法和其他方法在未知评分预测方面的差异,采用了均方根误差(RMSE, root-mean-square error)评估方法. RMSE的表达式为
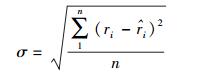
|
其中:ri为物品的真实评分,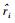
实验中把Native方法与目前最好的一些改进方法进行了对比,对比的方法包括协同过滤方法(CityBlock距离相似度、Pearson距离相似度)、矩阵分解方法(SGD方法、SVD++方法)及为目标用户随机产生邻居的方法(记为Random).其中,传统的协同过滤方法通过计算用户的User-Item向量的距离来寻找邻居;矩阵分解方法则通过建立拟合已有评分数据的矩阵模型来预测未知的评分;Random方法提供了一种基于邻居用户进行评分预测的方法的基础对照.本实验中用到的其他参数和方法设置:近邻数N=5,相似度量采用CityBlockSimilarity,评分预测采用式(1).
实验中采用的其他方法的实现均来自Apache Mahout(http://www.mahout.apache.org/),其中协同过滤方法以Random方法参考的邻居用户数和Native方法相同,矩阵分解方法SGD和SVD++的迭代次数为5 000.每种方法重复计算10次并取平均值作为最后的结果.不同算法的实验结果如图 3所示.

|
图 3 不同算法下的RMSE对比 |
由图 3的实验结果可知,Random方法效果最差,矩阵分解方法SGD、SVD++要优于采用CityBlock、Pearson相似性度量的传统协同过滤方法,而Native方法则具有最低的RMSE值,相比其他几种方法具有更高的算法准确率.
3.3 实验三:敏感性评估算法的敏感性主要是指数据集的稀疏程度对算法评分预测准确性的影响.好的推荐算法应当能适应不同稀疏程度的数据集.为了验证Native方法在处理稀疏程度不断增加的真实数据集时的优越性,进行了以下对比实验.首先对原始数据集中的评分数据进行随机抽样,使原始数据集的稀疏程度分别降低到0.5%、1.0%、1.5%、2.0%、2.5%、3.0%、3.5%、4.0%;然后对比不同算法在不同数据稀疏度情况下准确率的变化情况.实验结果如图 4所示.

|
图 4 数据敏感性对比 |
图 4中横轴表示数据集的稀疏程度(从左到右稀疏程度逐渐减弱),纵轴表示在相应稀疏度条件下算法的σ值,3条虚线分别表示对SVD++、SGD和Native方法结果的线性拟合.从图 4中可以看出,相比协同过滤方法和矩阵分解方法Native方法在不同稀疏度条件下均具有更低的RMSE值,即更好的准确率.矩阵分解方法随着数据稀疏性的增加算法的准确率逐渐下降(由SVD++和SGD方法的拟合曲线可以看出),说明矩阵分解方法是一种对数据集稀疏程度敏感的方法.而在实际应用中,随着用户和商品数量的不断增加,User-Item矩阵中有效评分数增长的速度远小于矩阵所能表示的评分的增长速度,从而User-Item评分矩阵会变得越来越稀疏(如淘宝数据集的稀疏度已达百万分之一),但矩阵中大部分用户的评分数则会随着时间的延长而有所增加.基于文中构建用户关于标签兴趣的方法可知,用户关注的物品越多计算用户关于标签的兴趣分布与用户的真实兴趣分布也越接近,因而利用因子分析方法计算的邻居用户也越精确.因此,算法的RMSE值也应当越来越低(当用户关于标签的兴趣分布未达到真实分布时)或者保持基本稳定(当用户关于标签的兴趣分布已逼近真实的兴趣分布时).针对上面的分析,实验中Native方法在用户具有较多的评分情况下(对应于图 4中数据稀疏度较低的情况,如4.0%,而在实际动态增长的数据集中则对应于稀疏度较高的情况)具有较低的RMSE值验证了这一点.所以在实际动态增长的数据集中,Native方法将会随着数据集的稀疏程度的增加,准确率略有提高或者保持基本稳定.
4 结束语针对实际应用中数据集稀疏度动态增加的特点,进行了深入的分析和研究,提出了一种基于标签和因子分解的协同推荐新方法,并通过在大量真实世界数据集上的实验,证实了所提出的方法在具有较好算法准确率的同时,对数据集的稀疏性具有较低的敏感性.然而,所提出的方法也存在一定的局限性,当数据集涉及的时间跨度较大时,标签系统也可能会有较大变化,基于标签的兴趣建模方法的准确性也会逐渐降低,从而影响算法的准确性.通过对标签系统进行及时跟踪,及时更新用户的标签兴趣变化将有助于保持预测的准确性.
| [1] | Tang Xiangyu, Zhou Jie. Dynamic personalized recommendation on sparse data[J].IEEE Trans. on Knowledge and Data Engineering, 2013, 25(12): 2895–2899. doi: 10.1109/TKDE.2012.229 |
| [2] | Chadha H, Jain A, Singh A, et al. Recommendation system for highly sparse datasets: a hybrid approach[C]//International Conference on Technology and Business Management March. Dubai: American University in the Emirates, 2014: 24-26. https://es.scribd.com/document/263747925/Journal-of-Computer-Science-IJCSIS-April-2015 |
| [3] | Yang Xiwang, Guo Yang, Liu Yong. Bayesian-inference-based recommendation in online social networks[J].Parallel and Distributed Systems, IEEE Transactions on, 2013, 24(4): 642–651. doi: 10.1109/TPDS.2012.192 |
| [4] |
周超, 李博. 一种基于用户信任网络的推荐方法[J]. 北京邮电大学学报, 2014, 37(4): 98–102.
Zhou Chao, Li Bo. A recommendation method based on user trust network[J].Journal of Beijing University of Posts and Telecommunications, 2014, 37(4): 98–102. |
| [5] | Lin Chiajen, Kuo Tsungting, Lin Shoude. A content-based matrix factorization model for recipe recommendation[C]//Advances in Knowledge Discovery and Data Mining. Switzerland: Springer International Publishing, 2014: 560-571. |
| [6] | Pan Ye, Cong Feng, Chen Kailong, et al. Diffusion-aware personalized social update recommendation[C]//Proceedings of the 7th ACM Conference on Recommender Systems. New York: Associate for Computing Machinery, 2013: 69-76. |
| [7] | Ren Jie, Zhou Tao, Zhang Yicheng. Information filtering via self-consistent refinement[J].Europhysics Letters, 2008, 82(5): 58007–58012. doi: 10.1209/0295-5075/82/58007 |
| [8] | Sun Duo, Zhou Tao, Liu Runran, et al. Information filtering based on transferring similarity[J].Physical Review E, 2009, 80(1): 017101–017104. doi: 10.1103/PhysRevE.80.017101 |
| [9] |
薛毅, 陈立萍.
统计建模与R语言[M]. 北京: 清华大学出版社, 2007.
Xue Yi, Chen Liping. Statistical modeling and R software[M]. Beijing: Tsinghua University Press, 2007. |


