基于笔者提出的弥聚子论的基本概念及其中对于主要反映超高速领域物质运动与时空之间关系的爱因斯坦狭义相对论(或称"高速狭义相对论")的尝试性拓展——预言了有可能显著存在于超低速领域的低速狭义相对论效应乃至有可能显著存在于超高速和超低速领域、同时涉及介于两者之间的常速领域的全速域狭义相对论效应, 对爱因斯坦狭义相对论的前提进行了评述、质疑与修正, 其要点包括:第一, 指出了爱因斯坦在"以狭义相对性原理为前提"的名义下所做推导的前提超出了纯粹意义上的狭义相对性原理, 它实际上隐含了独立且具有潜在局限性的"伽利略极限契合原理"和"线性时空变换假设"; 第二, 指出了依据对电磁波运动的考察和狭义相对性原理而得出的光速不变原理在其意义和作用方面存在一定的局限性, 而通过对实物体运动的考察则有可能获得等价于光速不变原理或较之更具普遍意义的能够作为狭义相对论前提的原理, 从而有可能更深刻、更充分地反映狭义相对论效应的物理本质乃至引发狭义相对论的变革; 第三, 区分了光速不变原理与"固有常数光速个例性原理", 指出了狭义相对性原理不仅寓于相关时空变换表达式的高度对称性之中, 还必寓于其他与物理过程相关的原理之中; 第四, 依据前期研究成果对狭义相对论的前提进行了更新, 即扬弃了光速不变原理并代之以先前提出的实物体运动存在速度上限和下限的"双极限速原理"及与之孪生的"双极限速质量-速度关联原理", 并指出了在笔者所期待的狭义相对论的变革中恰当运用"伽利略极限契合原理"或将其推广为"洛仑兹极限契合原理"乃至推广为扬弃具体极限情形的"一般性极限契合原理"以及放弃"线性时空变换假设"转而依循"时空变换数学形式的开放性原则"的必要性.在此基础上, 通过在上限速单极近似下引入质量-速度关联原理, 重新推导出了爱因斯坦狭义相对论中的洛仑兹变换关系式, 明确了以质量-速度关联原理取代光速不变原理的推演步骤, 并使得"光速不变"(或"上限速度不变")在爱因斯坦狭义相对论中由前提蜕变为推论.继之, 分别给出了上限速单极近似和下限速单极近似下质量-速度关系的唯象推导过程, 并明确了低速狭义相对论和全速域狭义相对论时空变换关系式的构建原则.这一工作使得全速域狭义相对论完备理论模型的建立又向前推进了一步.
Based on the fundamental concept of the author's bivergentum theory and therein the attempt of the extension of Einstein's special theory of relativity (or called as "high-speed special theory of relativity", ESTR or HS-STR), which shows the relationship between the matter movement and the space-time status mainly in the super-high speed regime, with the consequence of having predicted the low-speed special relativistic effect which may exist explicitly in the super-low speed regime and, furthermore, the full-velocity-scope special relativistic effect which may exist explicitly in both the super-high speed and the super-low speed regimes and also involves the in-between common speed regime, some comments, queries and modifications on the hypotheses of ESTR are made and the main points therein are as follows: First of all, it is pointed out that the so called "principle of special relativity (PSR)" which was adopted as one of the hypotheses in Einstein's derivation for the establishment of ESTR surpasses the purest-sense principle of special relativity, because it contains actually but implicitly the independent principle of Galileo-limit correspondence and the independent assumption of linear time-space transformation (TST), both being of, at least potentially, the lack of generality. Secondly, it is realized that the principle of constancy of light velocity (PCLV) which was revealed from the observation of the movement of electromagnetic waves as well as the PSR seems to be limited to some extent in its worthiness, while, based on the observation of the movement of the real physical objects, it would be possible to find some proper principle or principles which could be equivalent to or even more general than the PCLV so that could be taken as relevant hypothesis or hypotheses of the special theory of relativity (STR), and then more insightful and more comprehensive physical essences of the relativistic effects could be reflected and some significant changes of STR could be induced; Thirdly, the PCLV and the individual principle of intrinsic constant-velocity of light are differentiated, and it is found that the PSR resides not only in the high-level symmetries of relevant TST expressions but definitely also in other principles related to some physical processes; Fourthly, the STR hypotheses are updated according to the recent research advancements, i. e. the PCLV is sublated by replacing it with the previously proposed principle of upwards and downwards dual limitations of velocity which means that there exist both upper and lower velocity limits for real physical objects and also with the relevant twinborn principle of mass-velocity dependence (PMVD); Meanwhile, for possible changes of the STR expected by the author, the necessity of proper utilization of the principle of Galileo-limit correspondence or the extension from this principle to the principle of Lorentz-limit correspondence and even to the principle of general limit correspondence in which the concreteness of each individual limit is sublated and also the necessity of giving up the assumption of linear TST and turning to referring to the principle of the mathematical-form openness of TST are clarified. On the basis of these understandings, the expressions of Lorentz transformation in ESTR is re-derived by introducing the PMVD under the approximation of the mono-upwards-limitation of velocity; the concrete way to do this kind of derivations by replacing the PCVL with the PMVD is demonstrated; and, the observation of the constancy of light velocity (or, the constancy of the upper-limit velocity) is made to degenerate from a hypothesis into a deducted consequence in ESTR. Then, the phenomenological derivations of the mass-velocity dependences under the approximations of the mono-upwards and mono-downwards limitations of velocity are given respectively; the principles of the establishments of the expressions of TSTs in low-speed STR and in full-velocity-scope STR are also given. This work makes the establishment of the complete theoretical model of the full-velocity-scope STR go ahead for one more step.
笔者近年来所从事的弥聚子论研究[1-9]涉及对爱因斯坦狭义相对论(以下简称“爱氏狭义相对论”,也可称作“高速狭义相对论”)的拓展[3-5].笔者在对量子力学中的薛定谔波动方程加以适当拓展之后,未曾依赖光速不变原理即从理论上得出了2个重要的推论:① 实物体存在最大运动速度
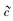
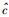
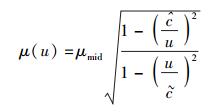
|
(1) |
其中:
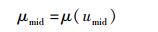
|
(2) |
可称作全速域狭义相对论基准质量,而umid则为全速域狭义相对论的中值基准速度.
由式(1)、式(2) 可解得
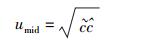
|
(3) |
可见,umid恰为实物体运动的上限速度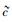
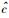
顺便指出,在文献[3]给出质量μ和速度u之间的关系时,已令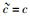
式(1) 的唯象推导过程则将在第3~5节中加以说明.
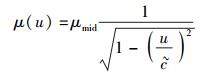
在上限速单极近似条件下,即当u趋近于上限速度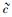

|
(4) |
显然,这与爱氏狭义相对论中的质量-速度关系(以下简称“质速关系”)表达式[10-13]
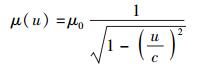
|
(5) |
差异甚微.
式(5) 中:
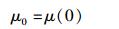
|
(6) |
为爱氏狭义相对论中的静止质量,即实物体运动速度为0时的质量.
比较式(4) 和式(5) 可知,只要在式(4) 中令

|
(7) |
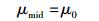
|
(8) |
立即可以得到式(5),反之亦然.也就是说,式(4) 和式(5) 在式(7) 和式(8) 给出的条件下是完全等价的.
实际上,只要承认实物体运动上限速度的唯一性和爱氏狭义相对论中光速为实物体运动上限速度的结论,式(7) 便立即得证.有鉴于此,在下文中如无特别说明将不再对记号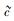
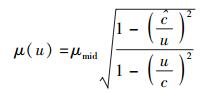
|
(1') |
式(1′)即是与文献[3]中首次出现的全速域狭义相对论质速关系表达式完全一致的表达式.正如上文中已经提到的那样,式(1) 则与式(1) 略有差别,其原因是在给出式(1) 时为了循序渐进地反映理论自身发展的逻辑而尚未考虑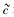
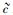
同时,只要在式(4) 中令速度u=0并运用式(6) 所给出的静止质量的定义,则式(8) 也便立即得证.这表明,在这里μmid和μ0是等价的.不过,需要注意的是,这种等价性只有在满足上限速单极近似的条件下才是成立的.此外,还有一点需要特别指出,按照低速乃至全速域相对论的观点,实物体的运动存在最小速度限制,其速度不可能为0,故严格而言应该不存在静止质量的概念,但因此处讨论的是实物体的运动速度u大大超过中值基准速度umid、当然也就大大超过下限速度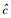
接下来讨论下限速单极近似下的情形,即u趋近于下限速度
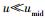
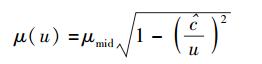
|
(9) |
式(9) 即低速狭义相对论中的质速关系.在式(9) 中令u=∞,可得实物体运动速度达到无穷大时的质量μ∞,即
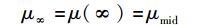
|
(10) |
亦即在满足给定的近似条件下,μmid和μ∞是等价的.
诚然,无论是按照爱氏狭义相对论的观点,还是按照全速域狭义相对论的观点,实物体的运动存在最大速度限制,其速度不可能为无穷大,故应该不存在无穷大速度下的质量概念,但因此处讨论的是实物体的运动速度u远小于中值基准速度umid、当然也就远小于上限速度c以至于高速相对论效应可予忽略的情形,故对无穷大速度和无穷大速度下的质量概念也均可不加排斥.
以上这些结论和表达式的给出对于全速域狭义相对论的建立是重要的,但仅凭这一点还不能说全速域相对论已经全面系统地建立起来了.如所周知,爱氏狭义相对论核心理论体系的建立是以2个相对做匀速直线运动的惯性参照系(以下简称“参照系”)之间的洛仑兹时空变换关系的确立(采用洛仑兹变换取代伽利略变换)为标志的.因此,只有在得出适用于全速域狭义相对论效应的时空变换关系之后,全速域狭义相对论核心理论体系的建立才算是真正完成了.正像洛仑兹时空变换关系的得出需要相应的前提(爱氏狭义相对论前提)一样,上述新的时空变换关系的得出也是需要给定前提的,不妨将该前提称作全速域狭义相对论前提.为此,需要重新审视爱氏狭义相对论前提的合理性及其表述乃至涵义的完备性,同时需要明确基于双极限速原理的质速关系在全速域狭义相对论中的地位和作用.在此基础上,即可给出藉以推导低速狭义相对论时空变换关系和全速域狭义相对论时空变换关系的前提、途径及原则.下文将依次探讨这些问题并给出最新的研究结论.
1 关于狭义相对论前提的探讨设有2个参照系S和S′,后者相对于前者沿x方向以速度v做匀速直线运动. S参照系中的三维空间坐标和时间坐标分别为(x, y, z)和t;S′参照系中的三维空间坐标和时间坐标则分别为(x′, y′, z′)和t′.相应的爱氏狭义相对论的时空变换关系——洛仑兹变换关系——的表达式为[10-13]
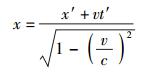
|
(11a) |
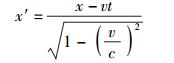
|
(11b) |
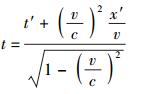
|
(11c) |
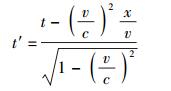
|
(11d) |
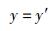
|
(11e) |
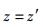
|
(11f) |
由于在y和z 2个方向上相对论效应对于空间位置坐标没有影响,所以在下文中将不再涉及式(11e)和式(11f).
为了对洛仑兹变换进行深入的讨论,兹给出比洛仑兹变换更具普遍性的变换形式:
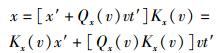
|
(12a) |
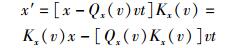
|
(12b) |
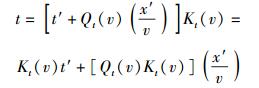
|
(12c) |
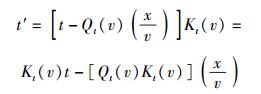
|
(12d) |
令
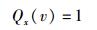
|
(13) |
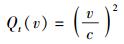
|
(14) |
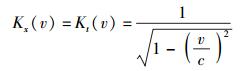
|
(15) |
式(12a)~式(12d)即蜕化为由式(11a)~式(11d)给出的洛仑兹变换关系.
为了方便起见,将Qx(v)、Qt(v)、Kx(v)和Kt(v)分别叫做空间偏移因子、时间偏移因子、空间胀缩因子和时间胀缩因子.
按照公认的说法,爱氏狭义相对论得以建立的前提有2个,即狭义相对性原理和光速不变原理.在爱因斯坦得出洛伦兹变换关系的推导中,这2个原理一并体现在如下的两组表达式中[10-13]:
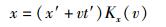
|
(16a) |
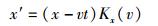
|
(16b) |
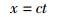
|
(17a) |
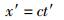
|
(17b) |
实际上,狭义相对性原理和光速不变原理既是相互独立的,又具有一定的关联性——后者可以被认为是前者与电磁理论相结合的产物,或者说前者部分地寓于后者之中.具体地,狭义相对性原理既主要体现在第1组表达式式(16a)和式(16b)中,又部分地体现在第2组表达式式(17a)和式(17b)中,因此狭义相对性原理与式(16a)和式(16b)并不完全等价;而光速不变原理则完全等价于第2组表达式式(17a)和式(17b),且如前所述,部分地包含了狭义相对性原理.这一“包含”关系将在下文中“对于光速不变原理的评述与质疑”部分做进一步阐述.
下面,首先分析和说明狭义相对性原理是如何由式(16a)和式(16b)体现的.
显然,除了式(16a)中“vt′”前面的“+”号和式(16b)中“vt”前面的“-”号彼此不同之外,式(16a)和式(16b)的形式对于参照系S和S′而言是完全对称的.这种对称性正是狭义相对性原理的反映.这种对称性同样存在于相应的伽利略变换关系式(在式(16a)和式(16b)中令Kx(v)=1即得)之中,而式(16a)和式(16b)与伽利略变换关系式的不同之处仅在于两式等号右端均多出了同样的因子Kx(v).这种因子配置的同一性是狭义相对性原理在时空变换关系式中特有的反映.
顺便指出,由于前文已经给出的式(12a)和式(12b)是与式(16a)和式(16b)相对应的、但更具一般性的表达式,故它们必以某种更具一般性的方式体现着狭义相对性原理.容易发现,在式(12a)和式(12b)中,除了“同一”地配置有因子Kx(v)外,还“同一”地配置有因子Qx(v),后者同样规范地体现了狭义相对性原理的要求.至于Qx(v)在式(16a)和式(16b)中没有以显性方式出现,则是因为该2式已包含了曾在式(13) 中给出过的Qx(v)=1的假定.此外,在式(12c)和式(12d)中的对应位置上分别“同一”地配置有因子Qt(v)和Kt(v),这同样是狭义相对性原理的体现.
前已述及,狭义相对性原理与式(16a)和式(16b)并不完全等价,或者说式(16a)和式(16b)只表达了狭义相对性原理中的部分涵义.循此细考,笔者又发现:作为狭义相对性原理的具体表达,式(16a)和式(16b)还有“涵义扩大化”之虞,它们实际上隐含了2个原本不属于狭义相对性原理的、因而应该明确地单独给出的附加限定条件(详见下文).为表述方便,笔者建议将带有这2个附加限定条件的、亦即“涵义扩大化”了的狭义相对性原理称作爱氏相对性原理,以区别于纯粹意义上的狭义相对性原理.
接着再来分析和说明光速不变原理是如何由式(17a)和式(17b)来体现的.显然,这2个式子极为明了地表达了在S和S′两个参照系中所观察到的同一束光是以完全相同的速度c行进的,故对于这2个式子而言确无深细考究之必要.然而,笔者发现,就光速不变原理本身而言,仍有一些问题值得详加探讨.譬如,在构建狭义相对论时空变换关系式时,这一原理所给出的信息是否足够深刻和充分地反映了狭义相对论效应的物理本质?它对于描述一般意义上的物理现象是否具有足够的普适性?它与式(16a)和式(16b)所表达的狭义相对性原理的内涵相结合是否足以保证相应的时空变换关系式的得出以及所有基本物理定律对于狭义相对论时空变换的协变性等.
以下分5个方面就上述这些有关狭义相对论前提的问题加以分析和探讨并提出相应的修订建议.
1) 爱氏狭义相对性原理中隐含的“伽利略极限契合原理”
狭义相对性原理是整个狭义相对论的基石,笔者对此极为认同.如前所述,式(16a)和式(16b)具有高度对称的数学形式,二者的时空胀缩因子Kx(v)和空间偏移因子Qx(v)(其值已设为1,故在式(16a)和式(16b)中未明显出现)都是同一的,因而符合狭义相对性原理的要求.但是,直接将Qx(v)的值设定为1,却已超出了狭义相对性原理的内涵.事实上,Qx(v)=1的要求可以从以下推导中得出.
将式(12b)代入式(12c)可得
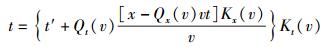
|
(18) |
整理后得
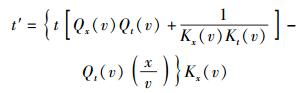
|
(19) |
对比式(12d)可知:
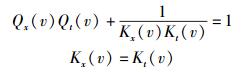
|
(20) |
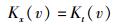
|
(21) |
为方便起见,可令
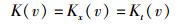
|
(22) |
式(20) 和式(21) 反映了时空变换关系式的自洽性要求.
再设某实物体在参照系S中沿x方向以速度ux运动,而在参照系S′中则沿x方向以速度u′x运动,则由式(12a)和式(12d)可得相应的速度变换公式,具体推导过程如下:
按照速度定义可以写出
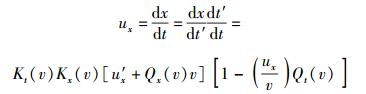
|
(23) |
整理后得
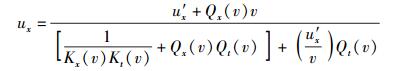
|
(24) |
将式(20) 代入式(24) 即得
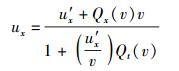
|
(25) |
式(25) 即所需的速度变换公式.
据式(25) 应有
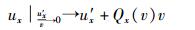
|
(26) |
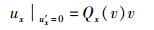
|
(27) |
由式(26) 可知,当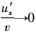

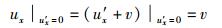
|
(28) |
对比式(27) 和式(28) 可得与式(13) 相同的表达式,即
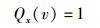
|
(29) |
这表明,Qx(v)=1实际上是在u′x=0时爱氏狭义相对论时空变换(洛仑兹变换)等同于伽利略变换这一前提条件所决定的,因此它超出了狭义相对性原理的范畴.它实际上是一个爱因斯坦没有言明却独立于狭义相对性原理而存在的前提,在此不妨将其称作“伽利略极限契合原理”.如果不给出这个前提,而只将Qx(v)作为一个与速度相关的未知因子来对待,那么由于未知量偏多,依据由式(12a)和式(12b)表达的狭义相对性原理和由式(17a)和式(17b)所表达的光速不变原理将无法得出洛仑兹变换关系.可见,将“伽利略极限契合原理”从爱氏相对性原理中剥离出来,将其作为与狭义相对性原理并列的一个独立存在的前提既是合理的,也是必要的.
2) 爱氏狭义相对性原理中隐含的“线性时空变换假设”
在依据爱氏狭义相对性原理和光速不变原理得出洛仑兹变换关系的过程中,式(16a)和式(16b)实际上还隐含了另外一个前提,即x和x′之间的坐标变换属线性变换,亦即式中的x、x′、t和t′都只出现一次幂项.这又是一个独立于纯粹的狭义相对性原理的前提,可以将其称作“线性时空变换假设”.就研究工作的一般规律而言,对于较为复杂的问题,唯象地采用尽可能简洁的表达方式,以期试探性地得出所需物理定律的数学表述,不仅是可以的,而且往往是必要的.至于所得出的结果的正确性,首先可以通过结果本身是否自洽及是否与基本原理相悖(譬如是否可以保证基本物理定律对于所得时空变换关系式的协变性)来检验,最终则要靠实验来检验;而一旦这些理论和实验检验表明结果有误,即应对x和x′之间坐标变换的数学表达形式进行适当修正,并重做理论推导,以得出更为接近客观实在的结果.因此,在爱氏相对论建立的过程中,将线性时空变换假设作为其前提本无可厚非;但是,将这一假设隐含在爱氏狭义相对性原理之中,而对其独立性不予指明则系缺憾.有鉴于此,将这一假设也从爱氏相对性原理中剥离出来,将其作为与狭义相对性原理并列的又一个独立存在的前提同样是合理的和必要的.
爱氏狭义相对论问世以来,线性时空变换假设的正确性或有效性和整个爱氏狭义相对论的正确性或有效性一起不仅被理论检验所肯定而且被大量实验所证实,但由于线性时空变换假设只是从式(16a)和式(16b)彼此之间的对称性上或其中相关因子配置的同一性上来体现狭义相对性原理,并未触及物理现象的具体过程及其多样性,因而它未能完全承载狭义相对性原理的全部使命,特别是未能承载保证所有基本物理定律对于基于这2个表达式所能得出的时空变换具有协变性的使命.事实上,在爱因斯坦得出爱氏狭义相对论的推导中,线性时空变换假设的这一欠缺是由部分地包含了狭义相对性原理涵义的、引入了与电磁学领域基本物理定律相关的重要信息的光速不变原理所弥补的.同时,还应当注意到,证实线性时空变换假设正确性或有效性的那些实验对于现实物理世界特征的反映是否完备并无确证,因此这些实验论证只是确凿性地表明了该假设对于得出高速狭义相对论是适宜的,而并未确凿地表明该假设对于推导低速狭义相对论、乃至全速域狭义相对论的时空变换关系式也是适宜的.此外,即使是仅就高速狭义相对论而言,线性时空变换假设所取得的成功也只能算是一种带有试探性和巧合性的成功,因为在做出这一假设之时并不掌握从该假设出发必定能达致成功的任何依据.基于上述认识,明确地指明线性时空变换假设的独立性就更为必要.
3) 对于光速不变原理的评述与质疑
如前所述,光速不变原理被公认为狭义相对论得以建立的另一块重要基石.像狭义相对性原理一样,它在狭义相对论理论体系中充当着“公理”的角色.尽管这一“公理”的依据相当坚实,但并非没有可商榷、可质疑和有待澄清之处.兹将笔者的具体观点陈述如下:
第一,爱因斯坦是依据电磁理论提出光速不变原理的,他指出:“麦克斯韦、洛仑兹方程的一个推论是:至少对于一个确定的惯性系K,光以速度c在真空中传播;于是必须认为这个推论是证实了的.按照狭义相对性原理,还须假定这个推论(注:此处“推论”二字为笔者所改,文献[10]中的原文为“原理”)对于每个其他惯性系的真实性. ”[10]这正是上文中断言光速不变原理是狭义相对性原理“与电磁理论相结合的产物”的理由.在这里,“电磁理论”的具体含义是在作为个例的某一既定参照系(爱因斯坦所称的“惯性系”)中“光以速度c在真空中传播”的推论,不妨将其称作“固有常数光速个例性原理”.在爱因斯坦的上述表述中,有关该推论本身的那个“必须认为”立论严谨,依据充分,且不带来任何理解上的困难;然而,有关该推论普适性的那个“还须假定”(光速对于任何参照系而言都是不变的)却极易给人们带来困惑——尽管从理性的角度来看,它是无可置疑的,但从感性的和经典力学的角度来看,它就显得非常怪诞,它与人们的常识、与人们所熟知的伽利略速度叠加原理是如此之相悖以至于让几乎所有初次接触相对论的人都感到费解.于是,在相对于伽利略相对性原理扩展了的适用于所有物理现象的狭义相对性原理和经典的伽利略速度叠加原理之间产生了不可调和的矛盾,正是这一巨大而尖锐的矛盾致使爱因斯坦意识到了人类时空观变革的必要性并大胆地提出了狭义相对论,从而绝妙地解决了这一矛盾.基于以上陈述,笔者认为,将“光速不变原理”这个经综合思辨得出的原理分解、还原为“固有常数光速个例性原理”和“狭义相对性原理”2个彼此独立的限定性论断,在逻辑上显得更为清晰.这样一来,爱氏狭义相对论的前提就可以归结为相互之间完全独立的4个限定性论断,即狭义相对性原理、固有常数光速个例性原理、伽利略极限契合原理和线性时空变换假设.当然,考虑到既有习惯,下文中还会继续沿用光速不变原理的结论和内涵,但是对于该原理的“可分解、可还原性”保持清醒的认识应该是必要的.
第二,有资料表明,爱因斯坦在创立狭义相对论时似乎并不知晓,至少是根本没有注意到迈克尔逊-莫雷实验.然而,该实验对于推动人类时空观进步的意义是显而易见的.诚然,人们尽可以对实验的精确性加以质疑,因为严格地说通过实验观测来判定一个物理量绝对没有变化是做不到的——任何测量仪器都有其极限分辨率,观测不到变化,并不见得实际上没有变化.换言之,也许变化是存在的,只是极小而已.但是,这一实验仍然可视作对狭义相对论时空观的有力支持,因为退一万步讲,它至少表明光速不变原理和爱氏狭义相对论时空变换(洛仑兹变换)关系是对客观物理规律的一种高度契合(哪怕只是近似)的反映,因而物理学对于光速不变原理和洛仑兹变换的认定应具有不可逆转性.
第三,一个自然科学理论的建立需要大自然提供相应的信息,狭义相对论的建立也是如此.狭义相对论效应起源于2个特定参照系之间的相对运动(匀速直线运动),故所需信息应与速度相关.由于2个参照系之间相对运动的速度是一个具有很宽值域的变量,故不同的物质运动形态所能提供的相关信息的多寡应与其涉及的速度范围有关.如前所述,人们已经公认电磁波在真空中传播的速度(光速)是一个固定值,且恰为实物体运动速度的上限值(同时也是参照系之间相对运动速度值域的上限值),而实物体的运动速度以及参照系之间相对运动的速度对于其自身值域则是完全覆盖的.据此,一个合乎逻辑的预期便产生了:实物体运动能够提供的有关狭义相对论效应的信息要比电磁波运动所能提供的相应信息来得丰富.然而,回顾狭义相对论的发展历程,实际情况正好反过来.在电磁理论出现之前,人们居然没有从实物体运动中得到任何有关狭义相对论效应的信息,其原因应该归结为在那个时期人们还一直没有机会借助于实物体的运动去领略高速物理世界的奇观.相比之下,电磁波的速度极高,因而当人们对电磁波运动规律的了解深入到某个程度的时候,高速物理世界里面的重要信息——光速不变——便显露了出来!于是,以往从实物体的常速(既非超高速,亦非超低速)运动中得出的、被人们奉为经典的伽利略时空变换关系便受到了挑战,全新的洛仑兹时空变换关系应运而生.可是,谁又能保证电磁波运动已经向人们提供了全部必要的信息呢?笔者认为,在有关实物体运动的理论发展到某个程度以及考察实物体运动的实验手段达到某种程度之后,电磁波运动能够提供的信息(如光速不变),实物体运动也应该能够提供,甚至实物体运动还有可能提供更为丰富的信息,从而形成可资充实狭义相对论前提的新原理.若果真如此,光速不变原理就有可能被与之等价的新原理所替代,甚至有可能让位于提供了更多信息的新原理.因此,狭义相对论的发展有可能需要超越光速不变原理.
第四,早在爱因斯坦创立狭义相对论之前,洛仑兹为了解释“光速不变”现象就已经提出了洛仑兹变换.该变换已经包含了狭义相对论的精髓,事实上成为狭义相对论的奠基之作——无论是从物理意义上、还是从数学意义上讲都是如此.洛仑兹的缺憾仅在于没有抛弃以太观念,没有领悟到洛仑兹变换中已然包含的那些全新的时空观信息,没有及时捅破那层触手可及的“窗户纸”!爱因斯坦的过人之处恰恰在于大胆地抛弃以太观念并向传统的时空观发起挑战,进而将洛仑兹变换应用于实物体运动领域,由此得出了一系列反映狭义相对论效应的崭新而重要的结论.至于爱因斯坦从上文曾界定过的爱氏相对性原理和光速不变原理出发得出洛仑兹变换关系式的数学推导,其实并没有包含比洛仑兹得出洛仑兹变换关系式更多的工作.同时,这一推导没有指明(因而也就谈不上是否恰当地指明)洛仑兹变换与光速不变原理之间的因果关系.事实上,如果先承认洛仑兹变换关系,则借助于速度变换公式,立即可以得出光速不变的结论.也就是说,洛仑兹变换可以是“因”,而光速不变可以是“果”.反之,若认为光速不变是“因”,而洛仑兹变换是“果”,则从物理逻辑上是难以说通的.这是因为,在狭义相对论中,洛仑兹变换关系的构建并未涉及光波与实物体之间的相互作用,因而光波作为一种恰巧能以实物体运动的上限速度而运动的物质就似乎只具备“被观测者”的资格,“光速不变”本身并不是一种令万物适应于斯的“塑造”宇宙的力量,因为当人们考察那些成对的、相对做匀速直线运动的参照系中实物体的运动状态与轨迹时,完全可以不管这一运动是否有光波介入,甚至完全可以不管此时是否有光波存在.因此,“光速不变”充其量只能算是见证洛仑兹变换关系正确性的一个特例.依据该特例所包含的信息也许在某种情况下(譬如在只关注高速狭义相对论效应的情况下)就足以从数学上求解出相应的时空变换关系(譬如洛仑兹变换关系);但是,也许在另外的情况下(譬如在同时关注低速狭义相对论效应的情况下),面对同样的问题,即面对求解相应的时空变换关系(譬如全速域狭义相对论时空变换关系)的问题,则该特例就显得无能为力了,更遑论保证所有基本物理定律对于相应的时空变换的协变性了.由此可见,光速不变原理在狭义相对论中并不具备因果律意义上和一般意义上的“前提”地位,一旦有新的符合因果律或更具普遍性的“前提”出现,则光速不变原理就应该让位于那个新的“前提”.
综上所述,光速不变原理既有其真理性的一面,也有其可修订、可拓展的一面.仅就高速狭义相对论的特殊情形而言,光速不变原理在洛仑兹变换构建中发挥了画龙点睛的作用.它与式(16a)、式(16b)所表达的狭义相对性原理的内涵相结合,实现了狭义相对性原理内涵的完备化,进而借助于其自身所包含的固有常数光速个例性原理,结合伽利略极限契合原理和线性时空变换假设,给定了洛仑兹变换的具体形式.尽管如此,这一原理所给出的信息尚未足够深刻和充分地反映出狭义相对论效应的物理本质,它对于描述一般意义上的物理现象并不具有足够的普适性,因而对于全速域狭义相对论(既包含高速狭义相对论,也包含低速狭义相对论)的一般情形而言,它与类似于式(16a)和式(16b)所表达的狭义相对性原理内涵的结合已然无助于相应的时空变换关系式的得出,更无法保证其合理性.
4) 针对爱氏狭义相对性原理的狭义相对论前提的修订和拓展
在爱氏狭义相对性原理中,由前述“涵义扩大化”引入的线性时空变换假设具有明显的局限性,这一点在上文中已经提及.事实上,同样是由“涵义扩大化”引入的伽利略极限契合原理也具有明显的局限性.因此,有必要对它们做适当的修订和拓展.
就伽利略极限契合原理而言,笔者的观点如下:
第一,在爱氏狭义相对论中,该原理指的是洛仑兹变换关系与伽利略变换关系在有零速度出现时的低速端的契合,而一旦出现某种不同于洛仑兹变换的新的时空变换关系,则相应的伽利略极限契合原理的涵义就会发生变化,譬如对于拟构建的低速狭义相对论时空变换关系而言伽利略极限契合原理指的就应该是低速狭义相对论时空变换关系与伽利略变换关系在有无穷大速度出现时的高速端的契合;第二,一旦洛仑兹变换关系被某种新的且更具普遍性的时空变换关系(譬如拟构建的全速域狭义相对论时空变换关系)所取代,洛仑兹变换就应当转而成为新的时空变换的特例,换言之,新的时空变换所应满足的就应该是洛仑兹极限契合原理,于是伽利略极限契合原理就应该被洛仑兹极限契合原理所取代.考虑到这些可能的修订和拓展,应该就此类契合原理给出一个扬弃具体极限情形的、最具一般性的表述,笔者建议将其泛称为时空变换的“一般性极限契合原理”.
就线性时空变换假设而言,笔者的观点如下:
一般地,某种新的时空变换关系与爱氏相对论中的洛仑兹变换关系相比应有其特殊性,因而有可能要求采用较为复杂的数学表达形式;而某种新的、更具普遍性的时空变换关系则必定会包含较之洛仑兹变换关系更大的信息量,因而更有可能要求采用复杂的数学表达形式,于是由“线性时空变换假设”给出的那种以线性表达为特征的数学形式也许就不足以反映物理实在的复杂性,故而必须让位于非线性形式的数学表达.这个认识可称作“时空变换数学形式的开放性原则”,将它引入狭义相对论的前提之中以取代“线性时空变换假设”显然是必要的.此外,应该指出,第一,这些时空变换的数学形式毫无例外地必须体现狭义相对性原理,即其相关表达式必须具有前已述及的那种高度的对称性;第二,即使具备了这种高度的对称性,因其并未触及物理现象的具体过程及其多样性,它们仍然不是狭义相对性原理的完备载体,这种欠缺仍然需要由某个适当的限定条件来补足.
5) 针对光速不变原理的狭义相对论前提的修订
如所周知,质量是描述实物体性质最重要、最基本的物理量,故考察实物体的运动往往需要考察实物体的质量或与实物体的质量相关的其他物理量及物理过程.实物体的质量依循一定的规律随其运动速度的变化而变化,这一点曾经是但目前已不是爱氏狭义相对论独有的结论.正如引言中所述,笔者已在不依赖光速不变原理、亦即不依赖爱氏狭义相对论的前提下通过对薛定谔波动方程的拓展以及对牛顿第二定律的拓展分别地、殊途同归地得出了该结论.从这种变化规律出发推导狭义相对论的时空变换关系将比从光速不变原理出发做相应的推导更能反映实物体运动与时空之间相互联系的物理本质,也更合乎因果逻辑.为了方便,兹将这种变化规律叫做质量-速度关联原理(简称“质速关联原理”).应当注意到,就某一个特定的参照系而言,质速关联原理属于个例性原理,该个例性原理相对于狭义相对性原理具有完全的独立性;而就不同的参照系而言,依据狭义相对性原理,质速关联原理应具有同一性,故质速关联原理就变为普适性原理,显然该普适性原理相对于狭义相对性原理便不再具有完全的独立性.这里的个例性质速关联原理和普适性质速关联原理之间的关系恰如固有常数光速个例性原理和光速不变原理之间的关系.有理由相信,将超高速(或称“上限速单极近似”)情况下的质速关联原理引入狭义相对论前提之中,以之取代光速不变原理(或固有常数光速个例性原理,下同),应能得出高速相对论时空变换关系,即洛仑兹变换关系;而将超低速(或称“下限速单极近似”)情况下的质速关联原理引入狭义相对论前提之中,且扬弃因不必考虑高速狭义相对论效应而暂失其用的光速不变原理,应能得出低速狭义相对论时空变换关系;再将全速域(或称“双极限速”)整体情况下的质速关联原理引入狭义相对论前提之中,且将光速不变原理作为辅助验证条件,则应能得出全速域相对论时空变换关系.当然,在得出相应的时空变换关系之后,还必须验证其是否能够保证所有基本物理定律的协变性.这些内容恰恰是下文中将要重点研讨的问题.
2 上限速单极近似下质速关联原理的引入与洛仑兹变换的重建在上限速单极近似条件下,质速关联原理的表达式已在彼此等价的式(4) 和式(5) 中给出.此处将直接采用式(5).
以式(5) 取代光速不变原理,并依据上文所述的狭义相对性原理、伽利略极限契合原理和线性时空变换假设,可以重建洛仑兹变换关系式,具体推导步骤如下.
首先,由第1节可知,狭义相对性原理和线性时空变换假设已经体现在式(12a)~式(12d)中,进而也就体现在了由式(25) 所给出的速度变换公式中;同时,伽利略极限契合原理则已体现在了表明Qx(v)取值为1的式(29) 中.将式(29) 代入式(25) 即得体现伽利略极限契合原理的速度变换公式:
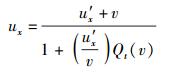
|
(30) |
其次,依据由式(5) 给出的质速关联原理,可以通过一个特殊设计的有关动量守恒定律的理想实验[13]来求得Qt(v)的表达式.在该理想实验中,仍设参照系S′相对于参照系S沿x方向以速度v运动,并设在参照系S′中存在一个质量为μ′的实物体,其运动速度用u′来表示.在某一刻,该实物体的状态因其内能突变而发生了变化:其初态为静止,即u′=0;其状态变化过程为由一个整体分裂为质量相等的A、B两部分,在分裂开始的那一瞬间其质量分别为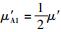
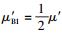
这样一个过程,在参照系S中看来则应该是,一个质量为μ的物体的状态因其内能突变而发生了变化,其初态为以速度u沿x方向运动.依据由式(28) 表示的伽利略极限契合条件可知,u=v;其变化过程仍然是由一个整体分裂为A、B两部分.在分裂开始的那一瞬间其质量彼此相等,分别为μA1=12μ和μB1=12μ,其速度相同,即为uA1=uB1=v;其终态为A处于静止状态(其速度uA2=0) 和B以一特定速度uB2沿x方向运动,二者的质量则分别变为μA2和μB2.这一过程也应符合动量守恒定律,即有
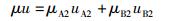
|
(31) |
同时,该过程还应符合质量守恒定律:
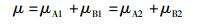
|
(32) |
故式(31) 变为
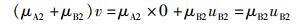
|
(33) |
另外,依据体现伽利略极限契合原理的速度变换公式(30) 可得
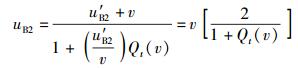
|
(34) |
于是,式(33) 变为
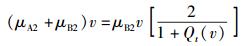
|
(35) |
解之得
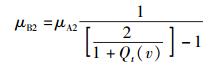
|
(36) |
再依据式(5) 和式(8),令u=uB2,μ(u)=μB2,μ0=μA2,可得
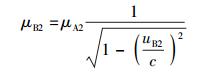
|
(37) |
比较式(36) 和式(37) 得
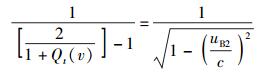
|
(38) |
将式(34) 代入式(38) 得
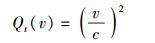
|
(39) |
至此,依据式(20)、式(22) 和式(29) 立得
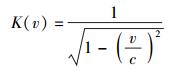
|
(40) |
将式(22)、式(29)、式(39) 和式(40) 代入式(12a)~式(12d)即可得出与式(11a)~式(11d)完全相同的上限速单极近似下的时空变换关系式,亦即爱氏狭义相对论中的洛仑兹变换得以重建.
将式(39) 代入式(30) 即得爱氏狭义相对论中的速度变换公式[10-13],即
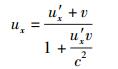
|
(41) |
再将参照系S′中的运动速度u′x=c代入式(41) 立即可得参照系S中对应的运动速度ux=c,也就是说光速不变原理或上限速度不变原理自然成立并由前提变成了推论.表面上看,本节推导所得出的结果与基于光速不变原理推导出的爱氏狭义相对论中的相应结果完全一致,但从实质上看二者之间存在着显著的差别,因为它们所依据的前提不同.若固守光速不变原理,爱氏狭义相对论是无法向低速和全速域狭义相对论拓展的,而采用质速关联原理取代光速不变原理则使得这种拓展成为可能.
3 上限速单极近似下质速关系的唯象推导第2节直接采用了引言中给出的上限速单极近似下的质速关系(等价于爱氏狭义相对论中的质速关系).兹就如何从上限速原理得出上限速单极近似下的质速关系给出说明.
上限速单极近似,意味着实物体运动的速度u足够高,即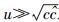
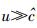
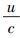
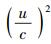
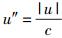
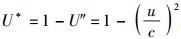
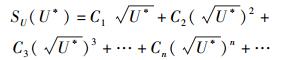
|
(42) |
其中C1、C2、C3、…、Cn…均为待定的常数系数.在这里,之所以要对形式宗量U*做降幂处理,是因为U*本身不是和u同次幂的量(它和u2是同次幂的量),只有做降幂处理才能保证级数项幂次集合的完备性.
于是,质量的表达式应为
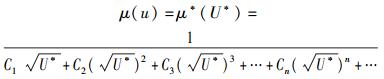
|
(43) |
若令四级形式宗量
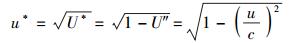
|
(44) |
则式(43) 还可以改写为
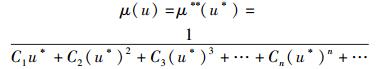
|
(45) |
显然,逐一确定式(45) 分母中每个级数项的系数是很难的,而物理定律通常应具有简洁优美的特征,因此笔者大胆地引入了一个唯象假定,即只保留其第1项就有可能与物理实在相符(为下文中叙述方便起见,可将此假定称作“最简形式假定”).这与其说是一个假定,不如说是一个猜想,故其正确性需要经过相关的实验或理论验证才能确认.
借助于这一假定,所需质速关系的表达式可以写作
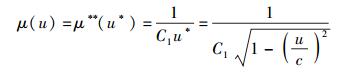
|
(46) |
由μ(0)=μ0可知:
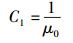
|
(47) |
于是有
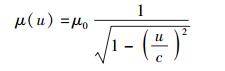
|
(48) |
这便是引言中由式(4) 及式(5) 给出且在第2节采用过的、可重新推导出洛仑兹变换关系的上限速单极近似下的质速关系.由于这一结果和爱氏狭义相对论中作为推论所给出的质速关系是一致的,而爱氏狭义相对论的正确性已经得到实验的证实,因而上文中提到的那个“只保留级数首项”的最简形式假定的正确性也就可以确认了.
4 下限速单极近似下质速关系的唯象推导与第3节中的推导类似,兹就如何从下限速原理得出下限速单极近似下的质速关系给出说明.
下限速单极近似,意味着实物体运动的速度u足够低,即

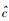
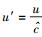
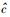
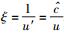
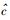
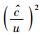
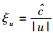

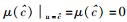
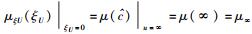

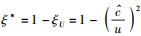

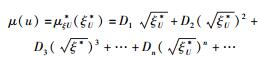
|
(49) |
其中D1、D2、D3、…、Dn…亦均为待定的常数系数.在这里,之所以要对形式宗量ξU*做降幂处理,也是因为ξU*本身不是和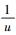
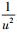
若令五级形式宗量
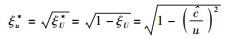
|
(50) |
则式(49) 还可以改写为
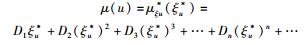
|
(51) |
在此,同样需要大胆地引入了一个唯象的最简形式假定,即只保留级数第1项就有可能与物理实在相符.自然,该假定的正确性也需要经过相关的实验或理论验证才能确认.
借助于这一假定,所需质速关系的表达式可以写作
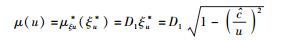
|
(52) |
由μ(∞)=μ∞可知:

|
(53) |
于是有
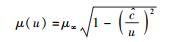
|
(54) |
这便是引言中由式(9) 及式(10) 给出过的下限速单极近似下的质速关系.在这里,需要特别说明的是,这一表达式的正确性尚未得到相关实验或理论的证实.
5 双极限速情况下质速关系的综合表达式对第3节和第4节得出的上限速单极近似和下限速单极近似情况下的质速关系加以综合即可得出双极限速情况下的质速关系.
不妨先从第3节中式(48) 表示的上限速单极近似下的质速关系出发来构建双极限速情况下质速关系的表达式.为此,需要设一个任意待定因子η(u),将它与式(48) 右端相乘,即可得到待定的双极限速情况下质速关系的表达式:
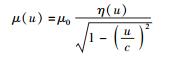
|
(55) |
当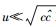
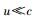
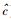
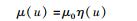
|
(56) |
据第4节所述,在上述条件下,质速关系的表达式应如式(54) 所示.
比较式(54) 和式(56) 可得
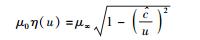
|
(57) |
将式(57) 代入式(55) 可得
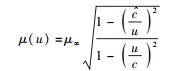
|
(58) |
对称地,不妨再从第4节中式(54) 表示的下限速单极近似下的质速关系出发来构建双极限速情况下质速关系的表达式.类似地可得
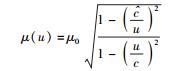
|
(59) |
比较式(58) 和式(59) 可知
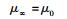
|
(60) |
于是,可以采用一个新的、统一的记号来表示这个基准质量值,即令
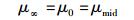
|
(61) |
式(58) 和式(59) 可统一改写为
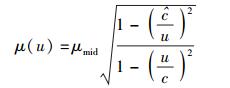
|
(62) |
此即双极限速情况下质速关系的表达式.若依据式(7) 令c=
在第2节中,笔者以上限速单极近似下的质速关联原理取代光速不变原理,重新推导出了高速狭义相对论时空变换关系式(洛仑兹变换关系式).类似的推导方法可以运用于低速乃至全速域狭义相对论时空变换关系式的推导.
如前所述,在高速狭义相对论效应被忽略不计的下限速单极近似条件下,光速不变原理不应再充当推导的前提而应予扬弃,取而代之的自然便是由式(9) 及式(10) 给出的该近似条件下的质速关联原理.在具体推导过程中,也还需要用到伽利略极限契合原理,只不过此时所言契合指的已不是在有零速度出现时的低速端的契合,而是在有无穷大速度出现时的高速端的契合.类比上限速单极近似下的情形,在下限速单极近似下,当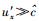
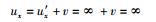
|
(63) |
然而,由速度变换公式(25) 可知,当u′x=∞时,有
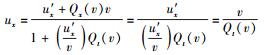
|
(64) |
比较式(63) 和式(64) 可得
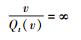
|
(65) |
亦即
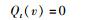
|
(66) |
于是式(25) 变为
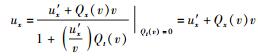
|
(67) |
令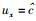
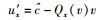
|
(68) |
因为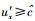
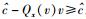
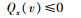
|
(69) |
由于Qx(v)=0意味着变换与v无关从而使变换失去意义,Qx(v) < 0(空间偏移因子为负)则意味着变换使得运动方向逆转从而与伽利略极限契合原理相悖,故推论Qx(v)≤0的得出实际上表明,在线性时空变换假设的框架内,不可能构建出低速狭义相对论时空变换关系式.因此,放弃“线性时空变换假设”转而依循“时空变换数学形式的开放性原则”来构建非线性时空变换关系式,即在时空偏移量的表达中适当引入高幂次项,遂成为题中应有之义.
非线性时空变换关系的一般表达式的构建须依据纯粹意义上的狭义相对性原理进行.在试探性地设定该表达式的基本形式之后,便可以依据上述相对性原理建立类似于式(20) 和式(21) 的相关变换因子之间的自洽关系;然后即可循第1节中所述的方法导出速度变换关系式,并可依据该关系式和在上文已提及的高速端伽利略极限契合原理,确定相关因子的具体表达式或相关因子之间的特定关系.若推演表明上述步骤无法完成,则需对时空变换关系的一般表达式进行重新设定,即应在其中引入更高幂次的非线性项,直到找到恰当的形式为止.继之,即可设计适当的类似于第2节中所述的理想实验以依据下限速单极近似下的质速关联原理确定所余变换因子的表达式,从而完成低速狭义相对论时空变换关系式的构建并确保其通过有关基本物理定律协变性的检验(必要时包括对时空变换关系式进行适当的完善).此外,还需指出的是,在此过程中,不排除对下限速单极近似下的质速关系表达式进行重新设定、即在式(51) 给出的级数表达式中取其前2项或更多项来构建该质速关系表达式的可能性.
在低速狭义相对论时空变换关系式建立之后,将它与洛仑兹变换关系式加以综合(包括引入新的与速度v相关的待定因子),并以纯粹意义上的狭义相对性原理、特定的时空变换极限契合原理、时空变换数学形式的开放性原则和双极限速质速关联原理为前提,以光速不变原理为辅助验证条件,应可最终得出全速域狭义相对论的时空变换关系式并使其通过有关基本物理定律协变性的检验(与前同理,必要时也包括对时空变换关系式进行适当的完善).这里所说的“特定的时空变换极限契合”指的是全速域狭义相对论的时空变换关系式在高速端须与洛仑兹变换关系式相契合,在低速端须与低速狭义相对论时空变换关系式相契合,而在中速段则须与伽利略变换关系式相契合.具体相关步骤此不赘述.
最后,还须补充说明一点:此前,笔者曾经尝试性地给出过全速域狭义相对论时空变换关系式(见参考文献[3]中的式(27a)和式(27b)),但当时还未曾仔细地考虑过全速域狭义相对论时空变换理论模型的构建问题,也未曾就那些关系式的正确性或合理性加以论证.因此,原则上那些关系式需要按照上述思路和原则重新给出.
7 结束语自从提出低速狭义相对论和全速域狭义相对论的质速关系以来,笔者一直在思考如何通过严格的数学推演建立低速狭义相对论和全速域狭义相对论时空变换关系式的问题.所幸如以上各节所述,在对爱氏狭义相对论及更普遍的狭义相对论的前提深细考究的基础上,实现这一目标的途径已经找到,其要点包括保持纯粹意义上的相对性原理不变,以笔者提出的低速狭义相对论和全速域狭义相对论质速关联原理(下限速单极近似质速关联原理和双极限速质速关联原理)取代光速不变原理,以时空变换的一般性极限契合原理取代爱氏相对论中隐含的低速端伽利略极限契合原理,以及用时空变换数学形式的开放性原则取代爱氏相对论中隐含的线性时空变换假设等.这一工作使得全速域狭义相对论完备理论模型的建立又向前推进了一步.
| [1] | Ren Xiaomin. Theoretical investigation on the continuous evolution of the electron-gas dimensionality: from bulk materials to quantum dots (postdeadline paper, AF4A. 6) [C]//2012 Asia Communication and Photonics Conference (ACP). Guangzhou: [s.n.], 2012: 1-4. |
| [2] | Ren Xiaomin. Modification of the theory on the energy-level dispersion and the continuity of the electron-gas dimensionality (invited talk / plenary session) [C]//21st International Symposium on Nanostructures: Physics and Technology (Nano). St. Petersburg: [s.n.], 2013: 347-349. |
| [3] | Ren Xiaomin. Novel understanding of electron states architecture and its dimensionality in semiconductors[J].Optics and Photonics Journal, 2013, 3(28): 322–330. |
| [4] | Ren Xiaomin. Started with the energy-level dispersion: the past one year (invited talk, track-1, AF4A.1)[C]//2013 Asia Communication and Photonics Conference, co-located and jointly organized with 2013 International Conference on Information Photonics and Optical Communications (ACP/IPOC). Beijing: [s.n.], 2013: 1-3. |
| [5] | Ren Xiaomin, Duan Xiaofeng, Liu Xiaolong, et al. On the validity of the newly proposed bivergentum mechanics: one ready-for-long evidence and two intriguing predictions (postdeadline paper, AF2A. 1) [C]//2013 Asia Communication and Photonics Conference, co-located and jointly organized with 2013 International Conference on Information Photonics and Optical Communications (ACP/IPOC). Beijing: [s.n.], 2013: 1-5. |
| [6] | Ren Xiaomin. Fundamental hypotheses: complex and anisotropic mass, full cosmic-scope uncertainty & wave-particle duality, and novel understanding of wave-function collapse (invited talk at the session of Interdisciplinary Sciences) [C]//The 8th Joint Meeting of Chinese Physicists Worldwide (OCPA8, also called as International Conference on Physics & Education-Looking Forward to Quantum Frontiers and Beyond). Singapore: [s.n.], 2014: 57. http://www.oalib.com/references/15823929 |
| [7] | Ren Xiaomin. From fractional dimensionality of electron-states architecture to unusual revelations in fundamental physics (invited talk, recorded in the Conference Program Guide)[C]//2014 International Symposium on Photonics and Optoelectronics (SOPO). Suzhou: [s.n.], 2014: 6-7. |
| [8] | 任晓敏. 能级弥散、分数维度电子态系与纳米光电子学(大会特邀报告)[C]//第九届全国光子学学术会议暨中国光学学会纤维光学与集成光学专业委员会成立30周年大会. 成都: [s. n. ], 2014: 10. |
| [9] |
任晓敏. 物质波动性与粒子性的科学表征及光子与姗子的相互转化[J]. 北京邮电大学学报, 2015, 1(38): 1–10.
Ren Xiaomin. Scientific characterization of wave property and particle property of matters and the mutual conversion between photons and symitons[J].Journal of Beijing University of Posts and Telecommunications, 2015, 1(38): 1–10. |
| [10] |
A爱因斯坦. 相对论的意义[M]. 李灏, 译. 北京: 科学出版社, 1961: 1-35.
Einstein A. The meaning of relativity [M]. Li Hao, translate. Beijing: Science Press, 1961: 1-35. http://www.doc88.com/p-7734799762709.html |
| [11] | 程守洙, 江之永. 普通物理学:第一册[M]. 3版. 北京: 人民教育出版社, 1978: 231-257. |
| [12] | 赵展岳. 相对论导引[M]. 北京: 清华大学出版社, 2002: 1-67. |
| [13] | 刘银春, 曾曦萍. 大学物理教程——实物与场[M]. 2版. 北京: 高等教育出版社, 2012: 88-110. |


