Contourlet变换能有效地应用在图像增强领域, 基于Contourlet变换的遥感影像融合算法常采用高频低频替换和频域线性加权两种融合方法, 因此, 通过粒子群优化算法对基于Contourlet变换分解不同子带图像所需的不同加权系数进行优化, 采用多元回归分析方法设定目标函数, 实现了全色影像与多光谱影像的融合, 与传统的Contourlet变换、PCA算法、高通滤波遥感影像融合算法相比较, 新方法在提高影像清晰度的同时在光谱保真度方面相对于其他算法有明显优势.
As a result of Contourlet transform can be effectively applied in the field of image enhancement, the characteristics of Contourlet transform in image fusion algorithm has been widely attention. Remote sensing image fusion algorithm based on Contourlet transform always utilize frequency domain linear weighted and swap high frequency to low frequency. By particle swarm optimization algorithm, the different weighting coefficients of different sub-band image by Contourlet transform is optimization. Using multivariate analysis method to set the objective function realizes the panchromatic image and multispectral image fusion. Compared with traditional Contourlet transform, (principal component analysis) algorithm, high-pass filter for remote sensing image fusion algorithm, the new algorithm with improving the definition of image have obvious advantages in terms of spectral fidelity than other methods.
遥感影像融合技术将不同空间分辨率和光谱分辨率的影像进行融合从而得到具有更好光谱分辨率和空间分辨率的影像,其目的在于综合地利用不同传感器所获得的影像,将各自的优势组合起来.根据融合的层次不同大致可分为3个级别:像素级、特征级和决策级融合,笔者对于Quickbird的全色影像和多光谱影像进行像素级融合,从而获得具有高空间分辨率的多光谱影像.
近年来,基于Contourlet变换的图像融合受到了广泛的研究和关注.笔者针对Contourlet变换在融合过程中不同子带图像的加权系数相对固定的方面进行了改进,通过粒子群优化算法的寻优特性对加权系数的值进行优化.
1 粒子群优化算法目前,粒子群优化(PSO, particle swarm optimization)是比较重要的群体智能算法之一,粒子群优化算法是继蚁群算法的另一重要的群体智能优化算法.
假定每个粒子(鸟群中单独的一只鸟)在特定的空间范围内都有自己的位置和速度,解空间中的每个点都与相应的粒子位置相对应,而每个粒子的飞行方向和距离都由该粒子的速度表示.粒子在解空间中运动通过跟踪个体极值和群体极值来更新个体位置.个体极值指个体所经历位置中计算得到的适应度值最优位置,群体极值指种群中的所有粒子搜索到适应度最优位置.粒子在每次更新位置的过程中都要计算适应度值,通过比较新粒子的适应度值和个体极值、群体极值的适应度值来更新个体极值和群体极值的位置,并通过个体极值和群体极值来更新自身速度和位置.设D维搜索解空间中xi=(xi1, xi2, …, xiD)T为对应第i个粒子的位置,vi=(vi1, vi2, …, viD)T为对应第i个粒子的速度,个体极值为pi=(pi1, pi2, …, piD)T, 种群的群体极值为pg=(pg1, pg2, …, pgD)T.
在每次迭代过程中,粒子通过个体极值和群体极值更新自身的速度和位置如式(1) 和式(2) 所示:
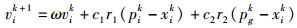
|
(1) |
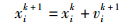
|
(2) |
其中: ω为惯性权重,k为当前迭代次数,vi为第i个粒子的速度,xi为第i个粒子的位置,c1和c2为加速度因子,r1和r2为分布于[0, 1]区间的随机数.
为防止粒子的盲目搜索,一般设置粒子的位置区间和速度区间.得到粒子新的位置后,可以求出对应的目标函数(或称为适应度函数)的值,并更新新粒子的个体极值位置信息和种群的极值位置信息.由于式(1) 可以更新前粒子的速度信息,提高了搜索范围,此外,粒子还可以通过对自己历史最优信息的学习和种群最优信息的学习,使得粒子群算法具有搜寻最优解的能力,粒子将会逐渐接近全局的最优解.
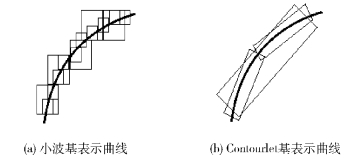
2 Contourlet变换近些年来,小波变换已经广泛用于图像融合领域,并取得了很多成果,然而二维小波基是由一维小波基张成的,小波变换在捕获图像边缘方向的能力方面比较有限,因此小波变换不能很好地表达图像特征. Contourlet变换可以捕获视觉信息中关键的几何结构特性. 图 1为小波基与Contourlet基对曲线的表示,Contourlet变换是一种多尺度和多方向的分解图像方法.
|
图 1 小波基与Contourlet基对曲线的表示 |
在整个Contourlet变换过程中使用拉普拉斯金字塔[1]进行多尺度分解,通过利用低通采样滤波器,得到与原始图像相似的低通图像,然后用原始图像与得到的低通图像相减得到差值图像,继续利用低通图像作为下一级分解的输入图像进行下一层金字塔变换,与低通图像经过低通采样滤波器得到图像相减得到下一层的差值图像.以此类推,可获取图像的方向信息,对图像的高频部分应用方向滤波器,能够很好获取图像的方向信息.将金字塔分解和方向滤波器组合,实现了Coutourlet变换.
3 基于粒子群优化Contourlet变换融合算法目前,基于Contourlet变换的全色影像和多光谱影像融合方法大致可分为两种:第1种方法为将全色影像和多光谱影像的每个波段都进行Contourlet变换,将变换得到的全色影像的高频部分分别替换多光谱影像每个波段的高频部分,最后对全色影像的高频部分与多光谱的低频部分进行Contourlet反变换得到融合的结果; 第2种方法与前面融合方法不同的是,将全色影像的高频部分与多光谱的高频部分进行固定数值的加权合成新的高频部分,全色影像的低频部分与多光谱的低频部分进行固定数值的加权合成新的低频部分,最后将合成的高频和低频部分经过Contourlet反变换最后得到融合结果.当第2种方法中的全色影像的高频部分加权系数取1和低频部分加权系数取0时,多光谱影像的高频部分加权系数取0和低频部分取1时即为第1种融合方法,在整个融合过程中加权系数人为设定,直接影响融合质量.本研究利用粒子群优化算法的寻优特性来优化多光谱不同波段与全色影像的加权系数,通过相应的目标函数来获得最优的加权系数,利用最优的加权系数来获得最后的融合结果.
对全色影像和多光谱的每个波段进行Contourlet变换,又变换获得的各个子带图像的加权公式为
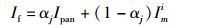
|
(3) |
其中:αj为第j个子带图像加权系数,α=(α1, α2, …, αD)T,其值由粒子群优化算法获得;Ipan为全色影像Contourlet变换的子带图像;Imi为多光谱第i个波段Contourlet变换的与全色影像子带图像对应的子带图像.
由于粒子群优化算法是寻找目标函数的解空间中最优解的过程,所以选取适当的目标函数尤为重要,文献[2]提出了对比两图像的扭曲程度的评价系数,文献[3]对文献[2]进行改进,通过引入超复数四元数的概念对多光谱影像融合进行评价判定,然而由于多光谱影像并不一定都是具有4个波段的影像,所以对于多光谱的每个波段和对应融合结果对应的波段采用式(4) 来计算相似程度.

|
(4) |
其中: x为多光谱第i个波段的均值,y为融合结果对应第i个波段的平均值,σxi为多光谱第i个波段的标准差,σyi为融合结果第i个波段的标准差,σxyi为多光谱和融合结果第i个波段的协方差. Qi取值越接近于1,表明两幅图片相似程度越高.
然而式(4) 并不能直接当作目标函数来进行融合,若简单与原始的全色影像和多光谱影像对比来作为目标函数,那么最优解结果将会得到原始的全色影像和多光谱影像,文献[4]提出了多元回归分析的方法用来评价融合算法.笔者利用多元方法来建立目标函数,在实验过程中对0.6 m×0.6 m的全色影像与2.4 m×2.4 m的多光谱影像进行融合,结果为0.6 m×0.6 m的多光谱融合结果,采用多元回归分析方法为,将0.6 m×0.6 m的全色影像重采样为2.4 m×2.4 m的全色影像,2.4 m×2.4 m的多光谱影像重采样为9.6 m×9.6 m的多光谱影像,利用2.4 m×2.4 m的全色影像和9.6 m×9.6 m的多光谱影像进行融合,将得到的融合结果与原始2.4 m×2.4 m的多光谱影像利用式(4) 作为目标函数,利用粒子群算法进行权值优化,将最优的权值应用到0.6 m×0.6 m的全色影像与2.4 m×2.4 m的多光谱影像加权的Contourlet变换融合.
4 融合结果及分析遥感影像融合的目的在于既保证多光谱的光谱信息,还没有完善的统一指标来融合质量,本研究针对通过计算融合结果与多光谱的相关系数和光谱扭曲程度用来判定光谱保真程度,计算融合结果的清晰度用来评价提高影像空间分辨率.
实验采用Quickbird影像,全色影像的分辨率为0.6 m×0.6 m,如图 2(a)所示,多光谱影像的分辨率为2.4 m×2.4 m,如图 2(b)所示为将其配准后重采样为0.6 m×0.6 m的分辨率影像,图 2(c)为高通滤波融合结果,图 2(d)为传统Contourlet变换融合结果,图 2(e)为PCA算法融合结果,图 2(f)为PSO优化的Contourlet变换.

|
图 2 不同算法融合结果 |
在客观评价方面,本研究采用相关系数和光谱扭曲作为相应的评价指标,虽然平均梯度可用来衡量图像的清晰程度,但在某些融合算法中产生随机噪声也会增大平均梯度值,因此在客观评价指标方面仅采用相关系数和光谱扭曲作为客观评价指标如表 1~表 3所示.
|
|
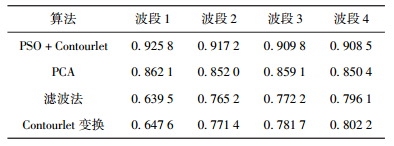
表 1 不同算法与多光谱相关系数 |
|
|
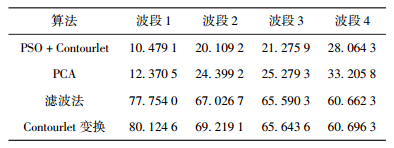
表 2 不同算法多光谱扭曲度 |
|
|
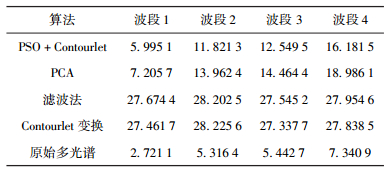
表 3 不同算法融合结果清晰度 |
从表 1可以看出,PSO优化的Contourlet变换融合算法结果与多光谱的相关系数最高,在光谱特性方面与多光谱相似程度最高.
从表 2可以看出,PSO优化的Contourlet变换融合算法结果的光谱扭曲程度最小,表明其在光谱保真特性上有明显优势.
从表 3可以看出,PSO优化的Contourlet变换融合算法结果在提高图像清晰度方面表现最差,然而随着图像清晰度的提高,融合结果引入的光谱畸变越大,在与原始多光谱清晰度对比发现,该算法在尽可能保证原始光谱特性的同时提高了图像的清晰程度.对比相关系数、光谱扭曲和融合结果清晰度表明,经过PSO优化的Contourlet变换融合算法在光谱保真方面优于PCA及其他融合算法,然而由于其较强的光谱保真能力,在提高图片的清晰度方面并没有其他融合算法表现突出.
研究结果表明,PSO优化的Contourlet变换的融合算法在保证多光谱的光谱信息同时又提高了图像的清晰度,且在光谱保真程度上尤为突出.
| [1] | Burt P J, Adelson E H. The Laplacian pyramid as a compact image code[J].IEEE Transactions on Communications, 1983, 31: 532–540. doi: 10.1109/TCOM.1983.1095851 |
| [2] | Zhou Wang. A universal image quality index[J].Signal Processing Letters, 2002, 9(3): 81–84. doi: 10.1109/97.995823 |
| [3] | Alparone L, Baronti S. A global quality measurement of pan-sharpened multi spectralimagery[J].Geoscience and Remote Sensing Letters, 2004, 10: 313–317. |
| [4] | Aiazzi B, Baronti S. Improving component substitution pansharpening through multivariate regression of MS + Pandata[J].Geoscience and Remote Sensing, 2007, 10(45): 3230–3239. |
| [5] | Heppner F, Grenander U. Astochastic nonlinear model for coordinated bird flocks[C]//The Ubiquity of Chaos. Washington: American Association for the Advancement of Science, 1990: 233-238. |
| [6] | Kennedy J, Eberhart R C. Particle swarm optimization[C]//Proc of the IEEE International Conference on Neural Networks. Perth: [s.n.], 1995: 1942-1948. |
| [7] | Miao Qiguang, Wang Baoshu. A novel image fusion method using Contourlet transform[C]//IEEE Communications, Circuits and Systems Proceedings. Guilin: IEEE, 2006: 584-552. |
| [8] | Wei Chuanming, Rick S B. Theoretical analysis of correlation-based quality measures for weighted averaging image fusion[C]//43rd Annual Conference on Information Sciences and Systems. Baltimore: IEEE, 2009: 363-368. |
| [9] | Tu T M. A fast intensity-hue-saturation fusion technique with spectral adjustment for IKONOS imagery[J].IEEE Geoscience and Remote Sensing, 2004, 10(1): 309–312. |
| [10] | Shi Wenzhong, Zhu Changqing, Zhu Caiying, et al. Multi-band wavelet for fusion SPOT panchromatic and multi-spectral images[J].Photogram Eng Remote Sens, 2003, 69: 513–520. doi: 10.14358/PERS.69.5.513 |
| [11] | Mumtaz A, Majid A. Genetic algorithms and its application to image fusion[C]//Proceedings 4th IEEE International Conference on Emerging Technology. Rawalpindi: IEEE, 2008: 6-10. |