2. 武汉大学 软件工程国家重点实验室, 武汉 430072;
3. 国家空管自动化系统技术重点实验室, 成都 610065;
4. 防空兵学院 指挥控制系, 郑州 450000
传统轨迹压缩算法要对每个具体轨迹进行建模与存储, 未利用路网对轨迹的限制, 故空间性能较差.针对该问题, 首先对路网空间进行建模, 继而探索个体轨迹的活动规律.提出基于轨迹的空间信息和轨迹的时态信息相结合的轨迹间投影距离度量(SRTD); 提出基于SRTD距离相似轨迹双层压缩算法(SDTC), 实验表明, SDTC算法相对于原始算法降低了存储空间开销; SDTC算法精度较原始算法有较大改进.
2. State Key Laboratory of Software Engineering of Wuhan University, Wuhan 430072, China;
3. National Key Laboratory of Air Control Automation System Technology, Chengdu 610065, China;
4. Air Defense Forces Academy, Zhengzhou 450000, China
The traditional trajectories compression methods handle each trajectory individually, but it does not take into account the actual route situations, so it shows limited space performance. To solve this problem, the route network model is designed, and regulations of these trajectories are deeply explored. The main contributions include: 1) proposing the distance measure SRTD (shadow reference trajectory distance) which incorporates the space and time information of trajectories together; 2) proposing an algorithm called SDTC (SRTD distance based trajectory compression), which compresses dual-layer trajectories based on SRTD distance similarities. Experiments show that, compared with traditional methods, SDTC algorithm significantly reduces the storage consumption, and is of good precision.
近年来随着基于位置的社交网络如Foursquare等的蓬勃发展以及带有GPS定位功能的智能移动设备的广泛普及,产生了大量需要存储和传输的轨迹数据. 在GPS轨迹数据压缩领域,目前已有很多相关的文献和算法.通过对原始轨迹进行线性拟合来减少轨迹点的数量是一个重要的研究方向[1-5],其中与Douglas-Peucker[2]相关的研究比较多.随后,Meratnia[3]指出Douglas-Peucker算法并不适合GPS轨迹数据,因为GPS轨迹数据同时具有空间和时间两个属性,而Douglas-Peucker算法在计算误差时忽略了轨迹的时态信息. Meratnia[3]提出一种新的距离计算方法同步欧式距离(SED, synchronous euclidean distance),且基于SED提出了一种新的自顶向下压缩算法(TD-TR, top down time ration).为了描述方便,统一把基于SED的轨迹压缩算法称为STC(SED based trajectory compression).
上述算法在轨迹压缩时,需对每条原始轨迹分别进行计算、存储,且未考虑路网空间的现实约束,因而压缩率较差、还原精度不高.针对上述问题,通过探索个人活动的活动规律及轨迹在路网空间的受限移动特征,提出了一种基于轨迹点投影的轨迹间距离度量,并基于该度量提出了一种双层轨迹压缩算法.实验表明,提出的方法在降低轨迹存储空间开销的同时,还能提高轨迹还原的精度.
1 基于轨迹点投影的轨迹间距离度量为了描述方便,先给出一些相关符号的形式化定义.
定义1 轨迹Ti. Ti={(x1, y1, t1), (x2, y2, t2), …, (x3, y3, t3)}表示一条轨迹,t1表示开始时间,tn表示终止时间,且满足t1<t2<…<tn.设|Ti|=n表示轨迹点的数目,且满足n≥1,Ti, j表示第j个轨迹点.
定义2 轨迹Ti的相邻轨迹点的距离集合SegDis(Ti)={s1, s2, …, sn-1},其中sj为轨迹Ti中的轨迹点Ti, j与Ti, j+1之间的空间距离,计算公式为式(1).规定SegDis(Ti,k)表示Ti第k段轨迹的长度.
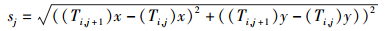
|
(1) |
定义3 轨迹Ti中由第1个轨迹点到第j个轨迹点组成的子轨迹的长度Length(Ti, j),其中j满足1≤j≤|Ti|其计算公式为式(2).设Length(Ti)表示轨迹Ti的轨迹总长度.
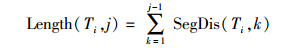
|
(2) |
相应的轨迹Ti中从第0个轨迹点开始的长度为d的子轨迹的最后一个轨迹点j=Index(Ti, d),j必须满足Length(Ti, j)≤d≤Length(Ti, j+1).
定义4 轨迹Ti中第j个轨迹点与第j+1个轨迹点所组成的子段中距离第j个点的空间距离为r的点JPoint(Ti, j, r),其中r必须满足如下条件:0≤r≤SegDis(Ti, j).
定义5 轨迹Ti中距离第0个轨迹点距离为e的空间点DisPoint(Ti, e), 计算公式为式(3), 其中e必须满足如下条件:0≤e≤Length(Ti).
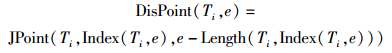
|
(3) |
定义6 轨迹Ti相对于轨迹Tj的基于轨迹点投影的轨迹间距离SRTD(Tj, Ti). SRTD(shadow reference trajectory distance)其意义是根据轨迹Ti的各个轨迹点与起始轨迹点间的距离,按照相应的距离在Tj中把按照定义5进行投影所得的点作为Ti中的相应点的替代点,所带来的最大误差.其中Tj称为参考轨迹,由于必须在Tj中找到与Ti所对应的轨迹点,所以两条轨迹的长度必须相同.
现实的GPS轨迹,相同路网段的轨迹数据的长度不一定是等长的.当被投影轨迹的轨迹距离大于参考轨迹的轨迹距离时,被投影轨迹的尾部的轨迹点不能在参考轨迹上找到相应的轨迹点与之对应,为了解决这个问题,引入轨迹间的长度因子
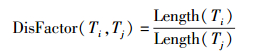
|
(4) |
引入轨迹间的长度因子之后,在计算两条轨迹的SRTD距离时,相应的轨迹间的SRTD距离计算公式为式(5),Eulers表示两点间的欧式距离.
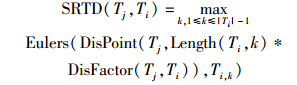
|
(5) |
定理1 引入距离因子后,计算轨迹Ti相对于轨迹Tj的SRTD值时能够在Tj中找到轨迹Ti全部轨迹点的投影点.从公式的定义可以看出原始轨迹Ti被投影后的轨迹点所组成的轨迹长度恰为Tj的轨迹长度,故证明从略.
2 基于SRTD距离的轨迹压缩算法给定某人在路网中的两条轨迹Ti和Tj,若Ti相对于Tj的SRTD(Tj, Ti)小于给定阈值α,则可以结合Ti中的轨迹点按照定义5、定义6的方法在Tj中进行投影,得到相应的投影轨迹Tp.这样Tp与Ti相对应的轨迹点之间的最大误差为α.因此可以只保留Ti中的相邻轨迹点间的距离及时态信息,利用Tj还原时最大误差为α.存储GPS轨迹点的传统方法需要保存所有轨迹点的经度、纬度和时间,代价较大,而这种方法只需要存储原始轨迹中相邻轨迹点的距离信息和时态信息,很好地节省了轨迹的存储空间.而且在保证精度的情况下,距离可以存为整数,而经纬度全部为浮点数,在进行存储时,这种方法需要的空间也更小.
基于上面的思想,提出了一个朴素的基于SRTD距离的轨迹压缩算法(N-SDTC,naive SRTD distance based trajectory compression).算法的基本步骤如下:
1) 计算待压缩的轨迹集合中任意两条轨迹之间的SRTD值,若该值小于给定阈值,则把相应的轨迹及其SRTD值加入候选集合;
2) 对于候选集合的轨迹按照SRTD值进行升序排列;
3) 选取其中SRTD值最低的轨迹按照图 1所示的数据结构进行压缩存储,并从候选集合中删除对应的两条轨迹;

|
图 1 SDTC算法压缩后轨迹的数据结构 |
4) 如候选集合不为空,继续第3) 步,否则程序结束.
在现实基于路网的GPS轨迹数据中,由于GPS存在一定的误差,且道路交通状况不同,并非所有位于相同路网中的轨迹都能够用一条基准轨迹表示.从后面的实验也可以看出,在误差相对较低的情况下,由于起始点的不同以及某些角度的差异,原始轨迹间的距离满足给定阈值的轨迹条数很少.因此,N-SDTC算法只适合理想的情况,不能对找不到基准轨迹的轨迹进行压缩,也不能对基准轨迹进行压缩.
由前述分析可知,两轨迹的SRTD值基本上是由两条轨迹的形状决定的,STC压缩算法能保留大部分轨迹的空间形态信息.因此,可首先利用STC算法对原始轨迹进行压缩,而后分析原始轨迹与其压缩后的轨迹,计算它们之间的SRTD距离.若距离满足给定条件,则用该压缩后的轨迹作为原始轨迹的基准轨迹.这样既可解决基准轨迹不能被压缩的问题,同时也能解决找不到基准轨迹时原始轨迹的压缩问题.这就是提出的双层压缩算法SDTC的核心思想,这里的双层一共有2层:第1层是利用STC算法先对轨迹进行简化压缩,第2层是利用NSDTC算法对简化后的轨迹进行压缩.
根据上述思想,双层轨迹压缩算法SDTC的基本步骤如下:
1) 采用STC算法对原始轨迹进行压缩;
2) 分别计算原始轨迹与被STC压缩后的轨迹的SRTD距离;
3) 对于距离小于给定阈值的轨迹按照N-SDTC算法压缩原始轨迹,与N-SDTC算法不同的是,被压缩轨迹的参考轨迹为采用STC算法压缩后的轨迹.
图 1给出了SDTC算法压缩后的轨迹数据结构示意图.基准轨迹的ID编号表示为2个字节的整形,轨迹的起始时间表示为4个字节的无符号整型,最后的部分共有N-1个2个字节大小的节点,N表示原始轨迹中轨迹点的数量.其中,第i个节点的前1个字节表示原始轨迹中的第i个轨迹段的长度,后1个字节表示原始轨迹中的第i个轨迹段的持续时间.
通过实验观察发现,在真实的GPS轨迹数据中相邻的轨迹点之间的速度往往比较接近,因此为了进一步降低空间开销,在不增加误差的前提下,可以把具有相近速度的相邻轨迹点进行合并. SDTC算法中采取一种基于动态窗口的启发式规则:若一个轨迹点的速度与窗口中所有轨迹点的平均速度相差小于给定阈值β,则把该轨迹加入窗口,否则对窗口中的轨迹点进行合并.经过轨迹点合并后的轨迹再计算SRTD距离,假设窗口中合并后的轨迹点在参考轨迹上相应的轨迹段上的速度是匀速的.
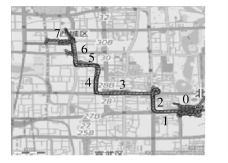
3 实验分析实验数据来源于微软亚洲研究院提供的Geolife[6]数据集.从编号为2的轨迹数据中选取如图 2所示的44条轨迹数据.编号为2的轨迹数据集共包括121条轨迹数据,去掉其中轨迹点数目小于300的数据后,剩余106条.其中与图 1所示的行为模式相似的轨迹共有52条,占轨迹总数的49%,从数据方面初步证实了提出的轨迹数据确实存在大量重复的事实.
|
图 2 Geolife中ID为2的个体部分行动轨迹 |
SDTC算法的第一层压缩算法采用的是TD-TR[4].为了消除增量表示方法给空间开销带来的影响,在进行对比试验时,对TD-TR算法压缩的轨迹也采用增量的方式进行存储.对图 2所示的1~6段各段轨迹分别采用两种算法进行压缩.实验共设计了7组不同的误差阈值,所允许的最大误差分别为5, 10, 15, 20, 25, 30, 40. SDTC对应的合并相邻的轨迹点的速度阈值β分别为0.5, 1, 2, 2.5, 2.5, 3.5, 3.5.
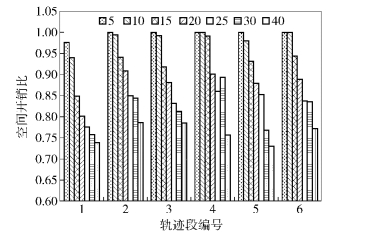
对能够找到基准轨迹的轨迹分别进行SDTC与TD-TR算法压缩,得到的存储空间开销比值如图 3所示.从图中可以看出,对于能够找到基准轨迹的轨迹,SDTC算法能在大部分情况下降低40%以上的空间开销. 图 4为SDTC算法与TD-TR算法的总空间开销比值.从图中可以看出,SDTC算法在TD-TR算法的基础上能够再降低10%~20%的存储空间开销,并且随着最大误差阈值的增大,能够降低更多的空间开销.

|
图 3 SDTC算法中能找到基准轨迹的轨迹与TD-TR算法空间开销对比 |
|
图 4 SDTC算法与TD-TR算法整体的空间开销对比 |
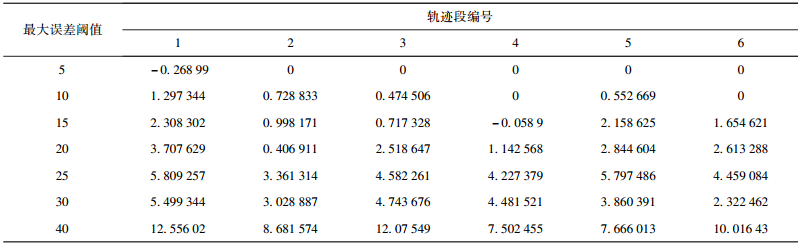
表 1给出了在不同的误差下,原始轨迹中能够被SDTC算法所压缩的轨迹与TD-TR算法压缩该轨迹所产生的误差的差值的平均情况.从表中可以看出,SDTC几乎都能够取得比TD-TR算法更小的误差,并且随着TD-TR算法误差的增大,SDTC能够降低更多的误差,提高算法的精度.
|
|
表 1 SDTC算法与TD-TR算法压缩产生的平均误差差值 |
针对个人活动的规律性以及路网空间中轨迹的空间形状规律性特点,提出了用SRTD距离来度量轨迹间进行映射时所带来的误差,并且基于SRTD提出了SDTC双层轨迹压缩算法,实验结果表明SDTC能在降低空间开销的同时,降低压缩所带来的误差.
| [1] | Meyer T. Essential dynamics: a tool for efficient trajectory compression and management[J].Journal of Chemical Theory and Computation, 2006, 2(2): 251–258. doi: 10.1021/ct050285b |
| [2] | Douglas D H, Peucker T K. Algorithm for the reduction of the number of points required to represent a line or its caricature[J].The Canadian Cartographer, 1973, 10(2): 112–122. doi: 10.3138/FM57-6770-U75U-7727 |
| [3] | Meratnia N, Rolf A. Advances in database technology-EDBT 2004[M]. Berlin Heidelberg: Springer, 2004: 765-782. |
| [4] | Cao Hu, Wolfson O, Trajcevski G. Spatio-temporal data reduction with deterministic error bounds[J].The VLDB Journal -The International Journal on Very Large Data Bases, 2006, 15(3): 211–228. doi: 10.1007/s00778-005-0163-7 |
| [5] | Muckell J, Hwang J H, Patil V, et al. SQUISH: an online approach for GPS trajectory compression[C] //Proceedings of the 2nd International Conference on Computing for Geospatial Research & Applications. [S. l. ]: ACM, 2011: 13. |
| [6] | Yu Zheng, Xie Xing, Ma Weiying. GeoLife: a collaborative social networking service among user, location and trajectory[J].IEEE Data Eng Bull, 2010, 33(2): 32–39. |