认知无线电(CR, cognitive radio)^[1]因其能够合理地利用宝贵的频谱资源而得到广泛研究. CR技术有效地解决了目前固定频谱分配方案下频谱资源短缺的问题.次级用户(SU, secondary user)动态接入空闲的授权频带(LFB, licensed frequency bands)时必须对主用户(PU, primary user)不产生干扰，这就需要SU准确地感知LFB的忙闲状态.因而，频谱感知技术成为CR的一项关键技术.传统的频谱感知技术研究主要集中在窄带频谱感知以及多用户合作感知上.近年来，宽带频谱感知开始受到广泛的关注，出现了一些相关文献^[2-3].在这些频谱感知算法中，以能量检测(ED, energy detection)^[4]最为简单高效且易于实现，而且不需要关于PU信号的先验信息.但是，由于对噪声功率进行估计时存在误差，所以ED在实际中的性能受到极大影响.

为了克服ED算法对于噪声功率信息的依赖性，提出了基于广义贝叶斯信息准则(GBIC，generalized Bayesian information criterion)的宽带频谱感知算法. GBIC准则是在传统的贝叶斯信息准则(BIC, Bayesian information criterion)的基础上提出来的，与传统的BIC相比，GBIC除了考虑采样数据的密度，还考虑了采样特征值的密度.目前关于GBIC准则的研究及应用不是很多.基于GBIC准则的宽带频谱感知算法是基于接收信号的协方差矩阵特征值和特征向量的信息，通过GBIC准则估计出LFB中被PU占用子带个数，从而判定宽带频谱占用情况.提出的基于GBIC准则的宽带频谱感知算法，在不依赖先验信息的条件下可有效地提高频谱检测性能.

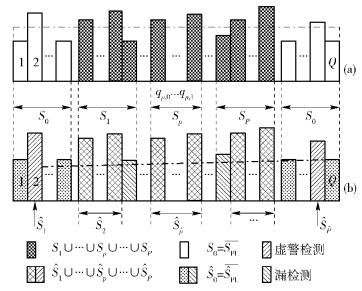
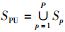
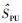
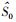
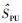
在宽带授权频段上，PU和SU分别以不同的优先级接入LFB. SU系统将宽带LFB(总带宽为WHz)分为Q个带宽相等的窄带子带，其中，被PU占用子带的集合为S_PU，空闲子带集合为S₀，如图 1(a)所示. CR系统中P个PU独立工作在宽带LFB上，且共占用M个子带；第p个PU占用子带集合为S_p={q_{p, 0}, q_{p, 0}+1, …, q_{p, 1}-1, q_{p, 1}}，其中，q对应于宽带LFB中的子带位置且有.假设SU完全未知PU信号结构及被占用子带数目及位置等信息.经宽带感知判决之后，得到PU占用子带集合，空闲子带集合，如图 1(b)所示.宽带感知的目标是使得与S_PU尽量一致，尽量避免虚警和漏检情况的发生.

图 1

图 1

图 1 宽带系统LFB上子带状态模型

宽带LFB上各个子带的检测问题，可采用二元假设表示，令H_{q, 1}表示第q个子带被占用的假设，H_{q, 0}表示第q个子带的空闲状态假设.因此，SU接收机接收到第q个子带的第n次快拍的感知数据y_q(n)为

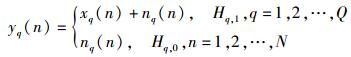
(1)

其中：x_q(n)=h_qs(n)且x_q(n)~CN(0, δ_{x, q}²)，s(n)为在第n时刻PU发射机发送的信号，h_q为信道增益系数，其中包含路径损耗、衰落及阴影效应等因素的影响. n_q(n)为高斯白噪声且满足n_q(n)~CN(0, δ_{n, q}²).假定x_q(n)和n_q(n)相互独立，N为频谱感知时间内的频谱感知快拍次数.

传统的宽带ED算法是一种独立子带阈值检测(ISTT, individual subband threshold test)判决，对于第q个子带有

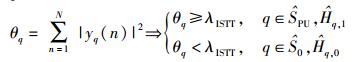
(2)

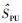
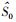
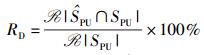
其中q=1, 2, …, Q，θ_q为感知时间内N次快拍得到的第q个子带的感知信号能量值，λ_ISTT为根据噪声功率信息获取的ISTT判决门限^[5]，由式(2) 判决得到宽带LFB子带状态判决集合为和.宽带频谱感知的性能评价一般通过检测率和虚警率来衡量.

(3)

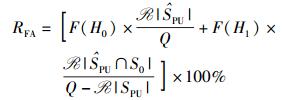
(4)

其中：|·|为集合的势，R_D为检测率，R_FA为虚警率. F(H₀)表示LFB所有子带均为空闲的概率，F(H₁)表示LFB至少有1个子带被占用的概率.

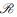
在SU接收端，第n次快拍时Q个子带采样信号可联合表示为

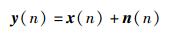
(5)

其中：y(n)=[y₁(n), y₂(n), …, y_Q(n)]^T为接收信号矢量；x(n)=[x₁(n), x₂(n), …, x_Q(n)]^T表示均值为0，协方差矩阵为G_x=E[x(n)x^H(n)]的独立同分布(IID, independent identical distribution)的循环对称复高斯(CSCG, circularly symmetric complex Gaussian)随机向量；n(n)=[n₁(n), n₂(n), …, n_Q(n)]^T表示IID、CSCG的加性噪声向量.文中的上标(·)^H，(·)^T分别表示向量或矩阵的Hermitian变换和转置.

接收端采样数据的协方差矩阵为

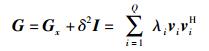
(6)

其中：G_x为接收端接收信号中PU信号分量的协方差矩阵；δ²I为噪声协方差矩阵，其中，δ²为噪声功率，I为Q阶单位矩阵.由于信号与噪声间的独立性，G为满秩对角矩阵，λ₁, λ₂, …, λ_Q和v₁, v₂, …, v_Q分别表示协方差矩阵G的特征值和特征向量.

假设有K(K=1, 2, …, Q)个子带被占用时，协方差矩阵的特征值λ_i(i=1, 2, …, Q)以降序排列，应满足如下关系：

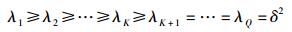
表明G的最小特征值具有多重性的特性. G通过以下方式计算：

(7)

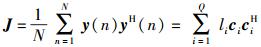
(8)

采样次数N越大，则J越接近G.当N→∞时，J为理想协方差矩阵G，l₁, l₂, …, l_Q和c₁, c₂, …, c_Q分别为采样矩阵J的特征值和特征向量.由于实际应用中，快拍数N有限，N次采样下协方差矩阵J的特征值l_q(q=1, 2, …, Q)降序排列关系变为

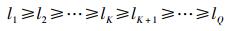
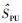
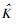
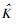
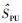
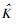
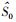
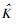
此时，采样协方差矩阵的最小特征值不再具有多重性.宽带频谱感知的目的是准确检测出整个LFB中处于被占用状态的子带，也就是确定各个子带的忙闲状态.被PU占用子带的瞬时功率为信号功率与噪声功率之和，而空闲子带的功率仅仅来自于噪声功率.因此，一般来说，瞬时功率大的子带更有可能被PU占用，应归属于集合.利用这一特性，如果已知子带被占个数，瞬时功率最大的个子带可视为被PU占用，属于集合，则剩余的Q-个子带属于集合.利用协方差矩阵最小特征值的多重性，可以准确计算出，但是由于采样数N的限制使得对协方差矩阵的估计总是非理想化精确的，因而这个方法难以实现.

假设有K个子带被占的情况下协方差矩阵表示为G^(K)，根据矩阵特征分解理论，协方差矩阵可以表示为

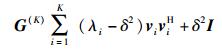
(9)

此时模型的参数向量为

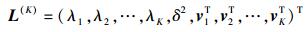
(10)

其中K=0, 1, …, Q-1.

对λ_i和δ²进行最大似然估计得

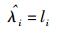
(11)

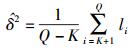
(12)

其中i=1, 2, …, K.则

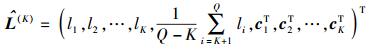
(13)

传统的BIC^[6]，有

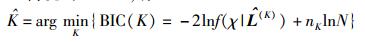
(14)

其中χ={y(1), y(2), …, y(N)}.

BIC的具体计算公式为

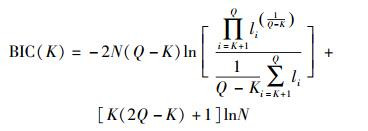
(15)

其中n_K=K(2Q-K)+1.

Stoica等^[7]给出了精确的BIC函数表达式为

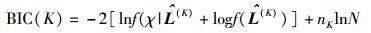
(16)

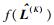
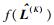
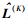
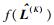
式(16) 中为模型参数向量的联合概率，式(16) 成立的条件是关于最大似然估计是平滑的且与采样次数N是独立的.式(16) 比式(15) 更为一般地表达BIC，即GBIC.式(15) 中BIC在一些情况(如低信噪比等)下不能达到满意的检测效果.为了提高性能，可考虑采用GBIC.与传统的BIC相比，GBIC除了考虑采样数据的密度，还考虑了采样特征值的密度.

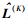
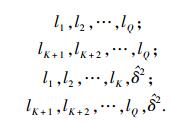
假设参数向量收敛于Z^(K)，则Z^(K)可采取以下组合：

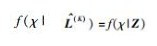
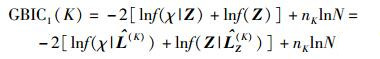
为了表示方便，后面用Z代替Z^(K)，有.则

(17)

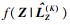
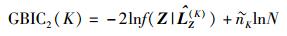
为了减少由特征向量引入的不确定性或仅考虑与特征向量独立的信息，从角度进一步地减少特征向量的影响，则有

(18)

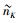
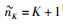
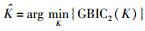
由于模型中参数向量被排除，所以比n_K小很多，且^[8]，则.

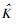
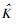
将GBIC准则应用于宽带频谱感知模型中，由GBIC信息准则估计PU个数，再利用ED方法计算各个子带上功率的大小并按降序排列，选出个功率较大的子带作为PU所占的子带，从而便于SU接入频带上空闲的频段，提高频带利用率.下面解决式(18) 的问题.

原则上，与由采样特征值推导得到的统计信息相比，所有采样特征值的联合密度包含了最丰富的统计信息，所以(18) 式可转化为

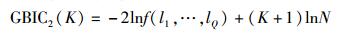
(19)

根据文献[9]中定理，有

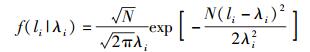
(20)

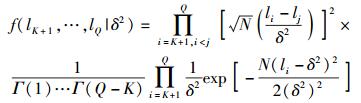
(21)

i=1, 2, …, K且N≫Q.

由于λ₁, λ₂, …, λ_K和δ²在实际中未知，所以采用贝叶斯方法解决上面的式(20) 和式(21) 中的λ_i和δ².假设不确定的参数为一个先验密度(如Jeffreys先验等)，且知道这些不确定参数的紧密间隔，再根据这些不确定参数的采样特征值的联合概率密度得到这些不确定参数.但是，此方法计算复杂度很高.在宽带系统模型下，信号和噪声服从独立同分布的高斯分布，且信号和噪声相互独立，利用最大似然估计λ₁，λ₂，…，λ_K和δ²，即根据式(11)、(12) 得

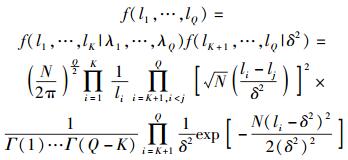
(22)

把式(22) 带入式(19) 中，可得

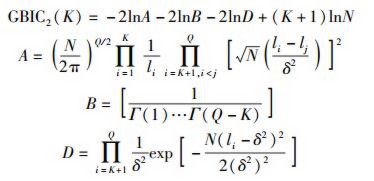
(23)

所以，估计被PU占用的子带数为

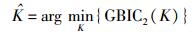
从上面的推导可以看出，存在K=Q的情况不能处理.对于这种情况，有两种处理方式：1) 这种情况可以看作单带感知处理，而对于单带频谱感知，Qing等^[10]介绍了许多方法；2) 实际应用中，该情况出现的概率很低，当检测到K=Q-1时，可近似认为全部子带被PU占用(K=Q)^[11].

所提出的方法不需要设置阈值或估计噪声功率，避免了不准确估计的干扰.因此，相比较ED，该方法在噪声不确定度方面具有更好的鲁棒性.尽管GBIC算法比Akaike’s信息准则(AIC，Akaike’s，information criterion)^[12]、最小描述长度(MDL, minimum description length)^[13]和BIC算法复杂度高，这一点从估计PU个数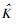上可以看出，但是GBIC中所有采样特征值的联合密度包含了最丰富的统计信息，因此相对于AIC、MDL和BIC算法，检测性能将大大提高.

GBIC算法的具体步骤如下.

步骤1 根据感知数据y_q(n)计算第q个子带上的感知能量值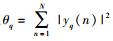，，q=1, 2, …, Q，将Q个子带上的能量值按降序排列，并记录各个能量值对应子带的位置.

步骤2 根据感知数据y_q(n)计算采样矩阵J得

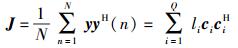
由式(23) 估计LFB上PU占用子带数为

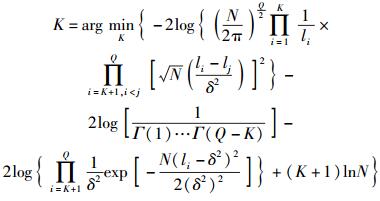
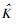
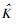
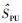
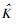
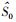
步骤3 根据判断各个子带上的PU占用情况，即较大个能量值的子带属于集合，则剩下的Q-个子带属于集合.最后，由式(3) 和式(4) 中的R_D和R_FA评估GBIC算法的性能.

采用Matlab仿真时，设定子带总数Q=64，被PU占用数K=20.考察GBIC算法性能与ISTT、AIC、MDL、BIC算法比较.各个算法的性能以检测率R_D和虚警率R_FA来衡量.其中，ISTT分为噪声不确定度为0 dB和1 dB，噪声不确定度α=10lnTdB，即噪声功率在区间[δ²/T, Tδ²]上服从均匀分布.根据文献[14]，IEEE 802.22要求理想的CR系统的检测概率和虚警概率分别满足R_D≥0.9和R_FA≤0.1.仿真中，为了满足实际应用要求，对于ISTT检测，固定R_FA=0.1，考虑α=0 dB和α=1 dB两种情况.

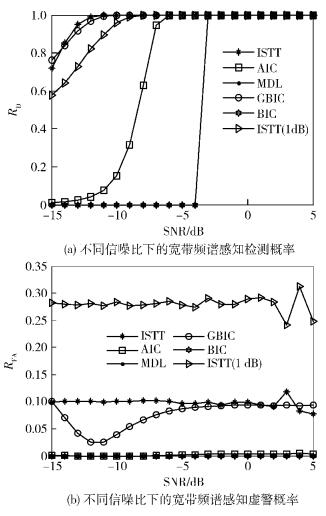
仿真1 根据GBIC₂(K)函数表达式成立的条件N≫Q，取采样次数N为8 000，图 2(a)和图 2(b)分别反映了在不同的信噪比下检测概率和虚警概率的变化曲线.从图 2的仿真结果可以看出，ISTT感知算法性能在α=0 dB时相对较好，但噪声不确定度对ISTT影响很大. AIC、MDL、BIC算法的R_FA近似为0，但是这些算法只有在一定的SNR区间上才能完成宽带频谱感知的目的，可见，AIC、MDL、BIC的检测能力受SNR影响较大. MDL和BIC的函数表达式相似，两者在性能表现方面具有一致性. GBIC感知算法在低SNR上检测能力与ISTT的检测能力很接近，同时GBIC感知算法的R_FA在SNR区间上很低，且随着SNR增大，R_FA趋于稳定，表现强的一致性.尽管AIC、MDL、BIC的R_FA很低，但是AIC、MDL、BIC在SNR为-10 dB时，R_D远远地低于0.9，而GBIC与ISTT感知算法已经十分接近，且R_D > 0.9.总体而言，仿真表明GBIC感知算法要优于AIC、MDL、BIC感知算法，且十分接近ISTT算法.

图 2

图 2

图 2 不同信噪比下的宽带频谱感知性能

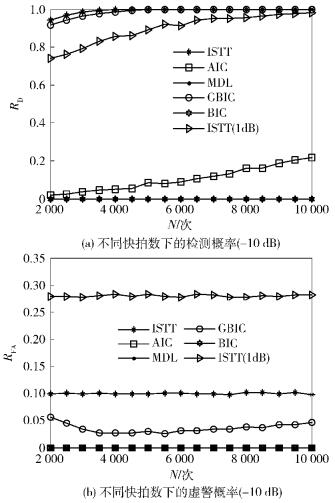
仿真2 由于各种算法的性能也受到采样数的影响，图 3反映了在SNR为-10 dB时，不同的快拍数下检测概率和虚警概率的变化曲线.从图 3的仿真结果可以看出，α＝0 dB时，ISTT感知算法性能相对稳定，但是受噪声不确定性影响的很大；不确定度α＝1 dB时，R_FA很高，而且R_D受信噪比墙^[15]影响不再升高.尽管AIC算法的R_D随快拍数增加而增大，但是即使快拍数达到10 000时其R_D仍太低，难以满足实际要求.尽管MDL、BIC的R_FA很低且接近于0，但是R_D也太低，也难以满足实际要求. GBIC算法的R_D要比AIC、MDL、BIC算法高很多，接近ISTT算法，同时GBIC在快拍数区间上R_FA很低，在实际应用中选取一定的快拍数就能满足文献[14]要求的R_D≥0.9和R_FA≤0.1这两个条件.仿真表明，即使在信噪比很低的情况下，GBIC算法也能有很好地检测性能，就整体性能而言，GBIC算法要远远地优于AIC、MDL、BIC算法，且十分接近ISTT算法.

图 3

图 3

图 3 不同快拍数下的宽带频谱感知性能

基于宽带频谱感知理论，提出了基于GBIC准则的宽带频谱感知方案.仿真结果表明，提出的感知频谱方案不仅能解决能量宽带频谱检测受噪声不确定性的影响，而且不依赖PU信号的先验信息，因此在实际中有很强的可实现性.