2. 青岛理工大学 理学院, 青岛 266033
针对量子网络节点在复杂信道环境中可靠广播通信的问题, 对其差错控制进行了研究, 提出基于前向纠错差错控制的量子网络广播通信协议.在N+1个量子节点构成的网络中主量子节点向N个从量子节点广播量子信息, 依据计算的误码数保留或删除在信息列表中从量子节点的信息, 利用纠错码内在特性纠正保留从量子节点量子态的比特翻转和相位翻转错误, 因为N个从量子节点测量基序列不同, 纠错后N个从量子节点有不同的密钥, 弥补了单个从节点泄密而造成整个网络泄密的不足.最后, 在理论上分析了信道利用率及协议安全性.
2. School of Sciences, Qingdao Technological University, Qingdao 266033, China
Considering the reliable broadcast communication problem of quantum network nodes in the environment with complicated information channels, the error control issue of this problem was investigated. A communication protocol with broadcast error control for quantum networks was proposed based on forward error correction. For networks containing N+1 quantum nodes, the error counts of N slave nodes are calculated respectively when the master node sends quantum information to N slave nodes, that determine that the slave nodes are retained in or removed from the information list according to the calculated error counts. For states of those retained slave nodes, the errors of bit flips and phase flips of the remaining slave nodes were corrected using the intrinsic characteristic of error-correcting code. Due to the different measuring sequences of the N slave nodes, each slave node has different quantum key. The problem of network leak resulted from the leak of single slave node, if all slave nodes have the same quantum key, can be amended. Finally, analyses of throughput efficiency of information channels as well as the protocol security were presented.
量子网络[1-2]是借助量子信道或量子计算等实现量子通信的网络系统,是量子信息学与经典网络通信相互融合的产物.单点对点量子通信协议有BB84协议、EPR协议、B92协议.在此之后,复杂量子网络的通信协议不断涌现,Yan等[3]提出多个量子节点中利用光子串编码的共享信息通信协议;周南润等[4]提出利用量子纠缠交换跨中心量子身份认证协议,延长通信距离并扩大认证范围;Ma等[5]提出利用GHZ态跨簇的多个量子节点共享密钥通信协议,扩展到3个簇的通信范围;Matsumoto等[6]提出在3个量子节点组成的量子网络中利用纠错码的量子通信协议.
文献[3-6]考虑多个量子节点通信与误码纠错的问题.在以上研究工作的启发下,笔者提出了在N+1个节点构成的量子网络中基于前向纠错差错控制的量子网络广播通信协议.
1 基础知识1.1 量子纠错码相关内容CCS(C1, C2)纠错码是根据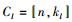
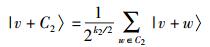
|
(1) |
式(1) 等号右边满足模2运算.
1.2 量子网络广播通信模型的相关内容主量子节点只有1个,记为S0. S0具备3个特点:① 该通信协议的核心成员,具有较强的处理量子信息能力;② 保存信息列表及通信后不同从量子节点的不同密钥信息,其中信息列表包括所有从量子节点特征的信息;③ 误码数检测某个从量子节点是否受到复杂信道环境干扰.
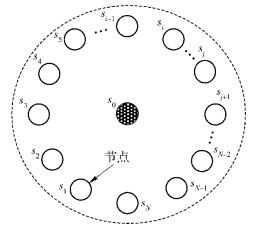
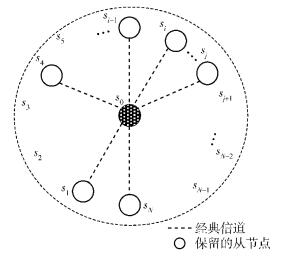
从量子节点有N个,记为S1, S2, …, Si, …, SN. Si(i=1, 2, …, N)具备4个特点:① 该通信协议的普通成员;② 根据协议设定情况数目可以动态变化;③ 具备唯一的特征信息,而且该信息便于S0收集处理;④ 分布位置具有随机性.主量子节点将信息发送给N个从量子节点,需要对信息加密,其中加密所需的密钥在4n+δ个量子态中获得.量子网络广播通信模型如图 1所示.
|
图 1 量子网络广播通信模型 |
主量子节点S0采用2组发送基Ⅰ与Ⅱ发送量子信息,其中发送基Ⅰ为{|0〉, |1〉},发送基Ⅱ为{|+〉, |-〉};从量子节点S1, S2, …, Si, …, SN也采用2组测量基Ⅰ与Ⅱ测量量子信息,其中测量基Ⅰ为{|0〉, |1〉},测量基Ⅱ为{|+〉, |-〉}.
2.1 信息初始化阶段S0向S1, S2, …, Si, …, SN发送量子比特,其表达式为|Ψ0〉=⊗k=14n+δ|ψpq〉,其中ψpq(p, q∈{0, 1})表示|ψ00〉=|0〉、|ψ01〉=|1〉、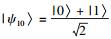
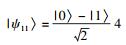
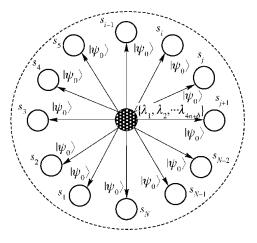
|
图 2 广播算法中分发信息 |
每个从量子节点Si接收广播分发的信息,并随机产生测量序列ρi,其表达式为ρi={ρi1, ρi2, …, ρi(4n+δ)};使用ρi测量从主量子节点发送过来的量子比特,其中ρij∈{0, 1}(i=1, 2, …, N,j=1,2,…,4n+δ),当使用测量基Ⅰ时记为0,反之记为1.如果Si正常收到量子比特,则按照顺序接收下一个;否则,通过公共信道向S0返回一个否定确认帧. S0收到否定确认帧后,再选择重传一次Si没有收到的量子比特. S0向从节点Si重传量子比特会影响协议的安全性,需要增加阈值检查机制,重传的次数要小于κ.阈值检查机制是要合理设定S0向Sd (Sd为任选的从节点)重传次数的极大值κ,如果大于κ,则S0中断与Sd的通信,并将Sd的特征信息从自己的信息列表中删除.
在公共信道上,S0宣布λ. Si根据λ的信息对照ρij,丢弃符合λj≠ρij条件的量子比特,即丢弃发送基和测量基不相同的量子比特.考虑该条件发生的概率,至少剩余2n个量子比特.因为每个从量子节点Si随机选择的测量基序列是不相同的,所以在基比对之后每个从量子节点Si所保留的测量结果是不相同的,故不同的从量子节点Si会有不同的密钥.如果不足2n个量子比特,则终止.
2.3 甄选合适量子节点阶段对于剩余的2n个量子比特,S0随机选取子集P⊂{1, 2, …, 2n}作为校验量子比特,并在公共信道上宣布,其中|P|=n. Si根据子集P测量手中的量子比特,并在公共信道上公告其测量结果.
每个从节点Si所保留的长度为2n的量子比特序列是各不相同的. S0分别与各从节点Si进行测量基比对后,从节点Si测量子集P时,所选用的测量基与主节点S0所选用的发送基一定是相同的.但是,由于复杂信道环境对量子比特的干扰,S0发送的比特与Si接收到的比特不一定是相同的,这样不相同量子比特的个数记为误码数,并用Ei表示,则有
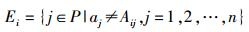
|
(2) |
其中:aj为S0发送的第j个量子比特的结果,Aij为Si接收到第j个量子比特的结果. S0与不同的从量子节点Si无法统一进行误码数校验,在2.5小节中每个从量子节点独立纠正误码信息;在主量子节点与每个不同的从量子节点之间,独立进行甄选合适量子节点的工作.
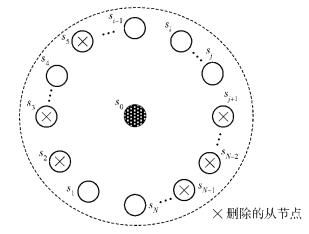
2.4 动态删除与保留从节点阶段根据误码数Ei来判别从量子节点Si是否被删除和保留.其一,满足Ei > κ条件的从量子节点,表明该节点因环境等因素的影响产生的误码过多,无法利用纠错码进行纠错,所以需要在信息列表中删除.假设N个从量子节点中S2, S3, S5, Sj+1, SN-2, SN-1的误码数均大于κ,用箭尾(×)表示删除该节点,如图 3所示.
|
图 3 广播算法中删除的从节点 |
其二,满足Ei≤κ条件的从量子节点在信息列表中保留,如图 4所示;利用CCS码进行纠错.假设从量子节点剩余的比特是vi,其表达式为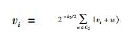
|
图 4 广播算法中保留的从节点 |
以保留的从量子节点中第i个接收量子比特为例,其中发生比特翻转和相位翻转分别记为eb、ep. S0在公共信道上公布校验矩阵H1、H2T,通过伴随式及H门操作,可知eb、ep错误,再利用反转操作获得纠正后的量子态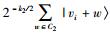
不同的从量子节点Si有不同的密钥,主量子节点S0需配备较大的存储空间,分别存储不同节点的密钥.这样不同从量子节点有不同的密钥,避免了因单个从节点泄密而造成整个网络泄密的问题.
3 信息传输中信道利用率分析S0发送一个量子比特的时间为ta,正常接收的条件下发送4n+δ个,故发送时间为(4n+δ)ta.考虑选择重传的量子比特为(4n+δ)Pd,故发送时间增加(4n+δ)Pdta.否定确认帧发送时延为tb,发送时间为(4n+δ)Pdtb.
Sj处理量子比特的时间为tc,接收量子比特所用时间tprj=(4n+δ)tc+(4n+δ)Pdtc.在实际系统中,不同的Sj对于P2是不同的,所以tprj不同,故考虑Sj处理量子比特的时间取tpr=max {tprj}, j=1, 2, …, N.假设控制信息长度为lh(比特),其发送时延为th.
成功发送4n+δ个控制信息所需的时间tf为
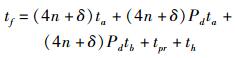
|
(3) |
协议中传输4n+δ位的数据帧与控制信息,其链路带宽为Γ=(4n+δ+lh)/tf,见文献[4].则信道利用率为
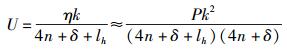
|
(4) |
考虑δ→0,n≫lh,式(4) 化简为
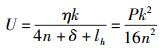
|
所以信道利用率与P、码元数k、码长n有关.
4 协议安全分析在通信协议中安全性取决于主量子节点和从量子节点之间分别直接通信的每个步骤.
1) 假设某从量子节点本身就是窃听者,想和主量子节点直接通信,获得发送信息.如果是这样,那么在第一部分就被发现,因为主量子节点到从量子节点广播信息均随机采用不同的测量基,非法从节点必定受到干扰和由于信道本身所产生的噪声,其引起误码数必定大于κ位,利用式(2) 使其在甄别阶段就可以完全剔除.所以保留从量子节点中存在窃听者是不可能的.
2) S0向各从节点Si重传量子比特,如果不设定重传次数,则通信协议存在不安全的隐患.因为窃听者可以截获S0向从节点Sd(Sd为任选的从节点)发送的量子比特,Sd在给定的时间内没有收到相关信息,必定返回一个否定确认帧,要求S0向Sd重传刚才的量子比特.窃听者对于第2次发送的量子比特不做任何处理,则量子信息无阻碍发送给从节点Sd.在这种情况下,窃听者就拥有了与Sd相同的量子比特,根据相同的量子比特,可进一步分析得到S0与Sd之间的密钥信息.但是,通过在2.2节中增加的阈值检查机制,就能有效地防止S0向各从节点Si重传量子比特导致的密钥泄露问题.只要重传次数大于κ,S0就中断与Sd的通信,并将Sd的特征信息从自身信息列表中删除,这样窃听者截获的包含Sd量子比特的信息就没有任何利用价值了.如果重传次数小于κ,则在2.3节中可视为误码,可利用纠错码的内在机制纠正,并不影响2.4、2.5节量子信息的处理.
5 结束语提出一种基于前向纠错差错控制的量子网络广播通信协议,实现量子网络中一对多的可靠广播通信.该算法使用现有的手段可以实现.另外,在一般的量子网络中应该有删除非法用户和添加合法用户的操作步骤.
| [1] | Gong Lihua, Liu Ye, Zhou Nanrun. Novel quantum virtual private network scheme for PON via quantum secure direct communication[J].International Journal of Theoretical Physics, 2013, 52(9): 3260–3268. doi: 10.1007/s10773-013-1622-3 |
| [2] | Hamada M. Reliability of calderbank shor steane codes and security of quantum key distribution[J].Journal of Physics A: Mathematical and General, 2004, 37(34): 8303. doi: 10.1088/0305-4470/37/34/009 |
| [3] | Yan Fengli, Gao Ting. Quantum secret sharing between multiparty and multiparty without entanglement[J].Physical Review A, 2005, 72(1): 012304. doi: 10.1103/PhysRevA.72.012304 |
| [4] | Zhou Nanrun, Zeng Guihua, Zeng Wenjie, et al. Cross-center quantum identification scheme based on teleportation and entanglement swapping[J].Optics Communications, 2005, 254(4-6): 380–388. doi: 10.1016/j.optcom.2005.06.002 |
| [5] | Ma Hongyang, Chen Bingquan, Guo Zhongwen, et al. Development of quantum network based on multiparty quantum secret sharing[J].Canadian Journal of Physics, 2008, 86(9): 1097–1101. doi: 10.1139/P08-047 |
| [6] | Matsumoto R. Multiparty quantum key distribution protocol without use of entanglement[J].Physical Review A, 2007, 76(6): 62316–62318. doi: 10.1103/PhysRevA.76.062316 |


