提出了一种复杂函数的可行域计算的仿射-区间方法.首先利用仿射-区间方法对设计域内函数的界限进行分析, 并利用分支定界法将该区域分类为可行域、不可行域和不确定域; 然后将不确定区域进行细分, 并对每个细分后的子区域再进行函数界限分析和分类, 直至子区域半径达到设计要求; 最后对所有可行域的面(体)积进行统计求和, 获得函数的总可行域.该方法可对非凸函数甚至可行域不连续函数的可行域进行估计.算例演示了该方法的计算过程, 并验证了该方法的有效性.
An affine-interval arithmetic-based method for the feasible region evaluation of function or electronic circuits was presented. This method uses affine-interval arithmetic to analyze the bounds of the function, and use branch and bound method divided these intervals into three kinds: accept regions, refuse regions and those of uncertain regions. All the uncertain regions were re-divided and the bounds calculation and classification performed again until the subintervals small enough. The statistics on each of accept regions was performed thereafter to get the sum of the accept regions. The proposed technique guarantees an efficient, reliable and accurate evaluation of the yield, even for non-convex and not simply connected feasible region. The examples presented show the features of the approach.
满足约束函数关系的所有可行解的集合即为可行域.当约束与目标函数均为线性函数时,可采用线性规划方法求解问题的可行域;当约束或目标函数为非线性函数时,可行域的求解有时较为困难.目前,国内外对非线性函数的可行域求解方法已做了大量的研究,包括神经网络方法、进化方法、线性矩阵不等式与多项式矩阵不等式组合方法等.特别是Spagnuolo等[1]利用区间算法并结合分支定界方法,对一种Sallen-Key带通滤波器的可行域进行了研究,得到了该带通滤波器的可行域和不可行域,为系统可行域求解提供了新思路.
参照文献[1]中的区间方法,笔者提出了一种复杂分布函数约束下系统可行域估计的仿射-区间方法.通过分析单纯的区间算法与仿射算法的优缺点,结合两者的运算特点,给出了一种函数界限运算的仿射-区间方法.首先利用仿射-区间方法在设计域内计算函数的界限,通过该界限与约束函数条件相比较,将设计域分类为可行、不可行及不确定域;然后将不确定区域进行进一步细分,并对每个细分后的子区域再进行函数界限分析及分类,直至子区域半径达到设计要求.该方法可以对非凸函数甚至可行域不连续函数的可行域进行运算.数值算例演示了该方法的计算过程,其结果验证了该方法的有效性.
1 区间算法与仿射算法的计算误差比较1.1 区间算法与仿射算法区间算术[2]是定义在区间上的一组运算规则.其主要特点是可处理不确定数据、自动记录计算机浮点运算中所产生的截尾和舍入误差、高效而可靠地估计函数在自变量区域的取值范围,从而被广泛应用于自然科学的各个领域.特别是近几年,区间算法也逐渐被引入系统的可行域[1]或可靠性分析之中[3]. Moore[2]给出了区间算术的定义:若以*表示加、减、乘、除这4种基本运算之一,则
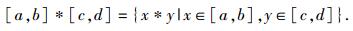
|
由此可见,区间算术的输入输出均为区间变量.
仿射运算是新近出现的处理不确定性问题的方法[4].与区间算术一样,仿射算术也能自动记录浮点数的截尾和舍入误差.此外,仿射算术还能自动记录各个不确定量之间的依赖关系.正是由于这个额外的信息,使仿射算术可得到比区间算术紧得多的区间,特别在长计算链中优势更加明显.仿射算术作为区间算术的一种改进形式,一经提出即被广泛应用于数值计算[5-6]、数值优化[7]、界限分析及可靠性计算中[8].
在仿射算术中,一个不确定量(区间)x可用一个仿射形式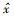
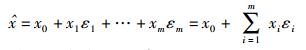
|
给定2个仿射形式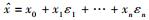
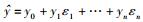
1)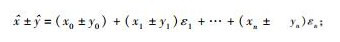
2)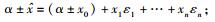
3)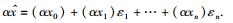
可见,对于线性运算,仿射运算不引入新的误差.而对于非线性运算,会引入新的误差,关于非线性运算的仿射算术可参见文献[8].
1.2 区间算法与仿射算法的计算误差比较对区间算法,误差的主要原因是忽略了变量之间的相关性,当算式中同一个变量出现两次以上时,变量之间的相关性就会对计算结果产生影响.如有区间变量xI=[1,2],函数
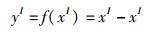
|
(1) |
区间计算的结果为yI=[-1,1],而真实值为[0,0].
对算式的等效变换可在一定程度上减小相关性对计算结果的影响,如xI=[1,2],函数
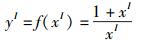
|
(2) |
用区间算法对该式进行计算,其结果为yI=[1,3],而该函数的精确解为[3/2,2].
当算式中每个变量只出现一次时,则可消除相关性对计算的影响,从而得到精确解.如对式(2) 进行等效变换后,可得
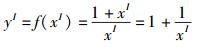
|
(3) |
据区间运算的相关规则,其计算结果即为精确解[3/2,2].
除了对算式做等效变换以外,还可以采用新的算法来考虑变量之间的相关性以及在运算中减小误差.仿射算法就是这样的一类算法,该算法可在一定程度上考虑变量间的相关性以减小运算误差,特别是在变量的一次项相关程度较高时更为明显.但不幸的是,仿射运算相对于区间运算在精度上的优势不是绝对的,如对非线性运算,特别是由乘除指数开方等构成的复合运算,误差的减小不是绝对的.这是因为仿射运算对非线性运算来说是使运算后变量变动的范围最小.如区间变量xI=[1,2],对函数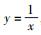
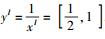
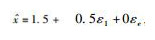
由此可见,由于仿射算法在处理非线性运算时会引入新的误差,所得的界限不一定比区间算法的运算结果紧凑.故在计算函数界限时,需要针对不同函数选取不同算法以期尽快获得尽量紧凑的函数界限.
2 可行域计算的仿射-区间方法既然仿射算法和区间算法在计算不同函数时各有利弊,有必要在计算时针对不同函数,将区间算法与仿射算法综合运用于给定函数,以提高求解效率和精度.仿射算法相对于区间算法,其最大优势在于能充分抵消变量之间一次项的依赖关系;而区间算法的优势则在于,当计算函数为单调函数时,区间算法可以准确地计算出函数的上下界.在给定函数上下界的求解过程中,根据给定函数的特点,将函数分解成多个不同的基本运算函数,再根据基本运算函数的特点,分别用仿射算法或区间算法对函数的界限进行求解.
现考虑如下普遍性的函数可行域计算问题:
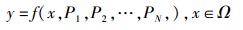
|
其中
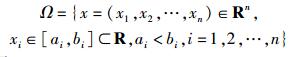
|
参变量:
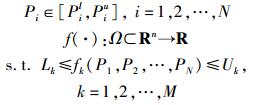
|
记:Ω为求解空间,Sa为接受域的集合,Sr为拒绝域的集合,Su为不确定域的集合,e为给定的计算精度.
以下给出利用仿射-区间方法进行可行域计算的具体步骤.
1) 初始化.令Sa=Ø,Sr=Ø,Su=Ω.
2) 在不确定域集合Su的每个子空间W上对fk(P1, P2, …, PN) (k=1, 2, …, M)进行仿射-区间运算,得到在给定子空间上的函数值上下限的仿射-区间扩张值:fku和fkl.
3) 空间分配.若子空间W上计算出的扩张值满足:
① Lk≤fkl且fku≤Uk,对所有的k=1, 2, …, M都成立,则将子空间W放入集合Sa中;
② Lu≤fkl或fku≤Ul,对任一k=1, 2, …, M成立,则将子空间W放入集合Sr中;
③ 否则,将子空间W放入不确定域集合Su中.
4) 若子空间W的半径大于给定的精度epse,转步骤5),否则转步骤6).
5) 空间细分.在每一维上对Su中的每个子空间W进行细分,并将细分后的子空间放入Su中形成新的不确定域的集合,转步骤2).
6) 统计.分别对集合Sa、Sr、Su中的每个子空间的面(体)积进行统计计算并求和,即可得到函数的可行域、不可行域及不确定域面(体)积以及在总面(体)积中所占的比例.
这种逐步细化的求解方法可以在一开始就将一部分空间划分到可行或不可行集合中,而只需对不确定域集合进行细分和进一步计算即可,如此可加速计算过程,使子空间半径尽快收敛.
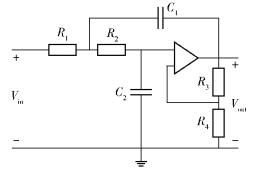
3 算例以图 1中的Sallen-Key带通滤波器为例说明本方法的计算过程.图中R5=1.98 Ω、R6=1.0 Ω、C1=0.1F、C2=0.1F等元件参数为固定值;而R3=[9.85,10.35] Ω、R4=[9.65,10.15] Ω为参数变动的区间变量.要求该滤波器的频率响应函数:
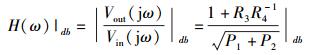
|
|
图 1 Sallen-key带通滤波器 |
其中
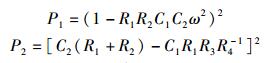
|
满足如下5个约束关系:ω=0.5 rad/s时,H(ω)⊆[11.5,12.5];ω=0.8 rad/s时,H(ω)⊆[10.0,19.0];ω=1.0 rad/s时,H(ω)⊆[40.0,50.0];ω=1.2 rad/s时,H(ω)⊆[16.0,17.0];ω=1.5 rad/s时,H(ω)⊆[7.0,8.0].试求区间变量R3和R4的可行域、不可行域及不确定域面积以及在总面积中所占的比例.
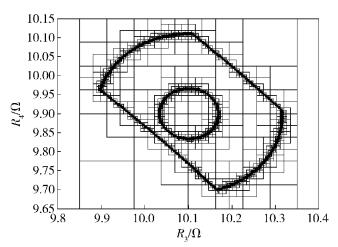
分别利用文献[1]中的区间方法和所提仿射-区间算法对该系统的可行域进行求解.在函数界限求解过程中,仿射-区间方法先利用仿射算法对频率响应函数中C2(R1+R2)-C1R1R3R4-1部分的函数界限进行求解,而后在其余运算中采用区间方法求解频率响应函数的界限. 2种方法求解过程中解空间的细分过程如图 2和图 3所示,图中的纵横坐标为别为R4和R3.
|
图 2 区间算法细分过程 |
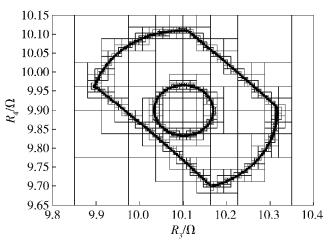
|
图 3 仿射-区间算法细分过程 |
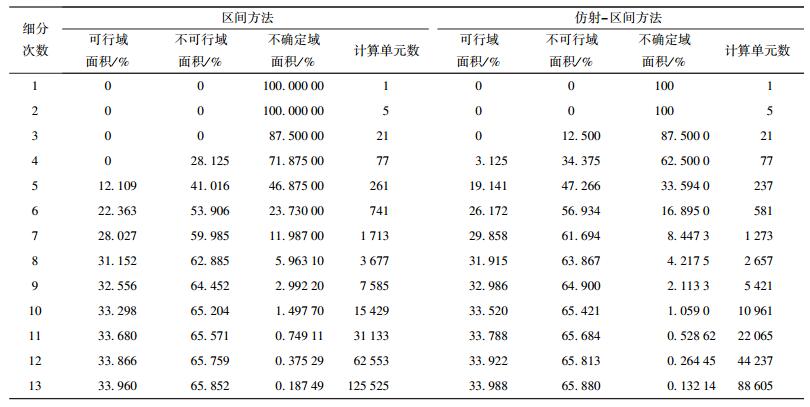
由图 2和图 3可以看出,利用区间算法和仿射-区间算法对给定函数的可行域进行求解时,随着区间的细分,不确定区域逐渐在可行域和不可行域的边界处累积,并最终形成深色的边界区域.由于采用的算法不同,从两图上可以看出两者收敛的过程是不同的,相比之下,仿射-区间算法的深色区域面积更小,不确定区域收敛的速度更快. 2种方法的收敛过程比较如表 1所示.
|
|
表 1 2种方法求解Sallen-Key滤波器可行域的区间细分过程 |
从表 1中可以看出,利用以上2种算法求解时,随着求解区间的细分,可行域和不可行域的面积均逐渐增大,而不确定域面积都逐渐缩小;区间分得越细不确定域面积将越小.但2种算法的求解效率不同,相比之下仿射-区间算法收敛得更快,在细分次数相同的情况下,不确定区域的面积更小,所计算单元的数量更少,效率更高.
4 结束语在非线性约束下,非线性目标函数的可行域难以求解,特别是当函数的可行域呈非凸、不连续等复杂分布时可行域的求解更为困难.所提出的仿射-区间算法与区间算法一样,都可以对复杂分布的可行域进行求解.
但仿射-区间算法收敛得更快,在细分次数相同的情况下,不确定区域的面积更小,计算单元的数量更少,效率更高.利用算例对2种算法进行了比较,并验证了仿射-区间算法的有效性.由于算例只用到了目标函数的表达式,并不针对于某一个具体的器件或者系统,故该方法亦可应用于其他任何一种显式目标函数问题的可行域求解,具有广泛的应用范围.
| [1] | Spagnuolo G. An interval arithmetic-based yield evaluation in circuit tolerance design[C]//ISCAS 2002, IEEE International Symposium on Circuits and System. Scottsdale, Arizona: The IEEE Circuits and Systems Society, 2002: 743-746. |
| [2] | Moore R E. Interval analysis[M]. New Jersey: Prentice-Hall, 1966. |
| [3] | Jorge E Hurtado, Diego A Alvarez. The encounter of interval and probabilistic approaches to structural reliability at the design point[J].Computer Methods in Applied Mechanics and Engineering, 2012, 225-228(15): 74–94. |
| [4] | Luiz Henrique de Figueiredo, Jorge Stolfi. Affine arithmetic: concepts and applications[J].Numerical Algorithms, 2004, 37(7): 147–158. |
| [5] | Vakili S, Langlois J M, Bois G. Finite-precision error modeling using affine arithmetic[C]//Acoustics, Speech and Signal Processing (ICASSP), 2013 IEEE International Conference on. [S.l.]: IEEE, 2013: 2591-2595. |
| [6] | Soares R P. Finding all real solutions of nonlinear systems of equations with discontinuities by a modified affine arithmetic[J].Computers and Chemical Engineering, 2013(48): 48–57. |
| [7] |
谢永强, 陈建军, 徐亚兰. 基于仿射算法的确定性全局优化算法[J]. 华南理工大学学报:自然科学版, 2012, 40(5): 35–40.
Xie Yongqiang, Chen Jianjun, Xu Yalan. Deterministic global optimization algorithm based on affine algorithm[J].Journal of South China University of Technology: Natural Science Edition, 2012, 40(5): 35–40. |
| [8] |
朱增青, 陈建军, 宋宗凤, 等. 区间参数杆系结构非概率可靠性指标的改进仿射算法[J]. 工程力学, 2010, 27(2): 49–58.
Zhu Zengqing, Chen Jianjun, Song Zongfeng, et al. Non-probabilistic reliability index of bar structures with interval parameters based on modified affine arithmetic[J].Engineering Mechanics, 2010, 27(2): 49–58. |