2. 北京航天测控技术有限公司, 北京 100041
提出了串联机构运动分析的Denavit-Hartenberg(D-H)四元数变换方法.给出了点的映射的四元数描述方法和相邻连杆间变换的D-H四元数变换方法, 建立了D-H四元数变换的矩阵演算方法, 构造出了机器人学中经典的D-H齐次变换矩阵, 证明了D-H四元数变换方法与D-H齐次变换矩阵方法的运动分析结果是一致的, 从而从理论上证明了所提出的D-H四元数变换方法的正确性.在相邻连杆变换的D-H四元数变换公式基础上进一步推广, 提出了任意个连杆的串联机构运动分析的D-H四元数变换方法.以PUMA机器人的运动分析为实例, 采用D-H四元数变换方法进行运动分析, 并验证了该方法的正确性和有效性. D-H四元数变换方法是串联机构运动分析的一种新方法, 具有几何意义明确和计算简单的优点.
2. Beijing Aerospace Measurement and Control Technology Company Limited, Beijing 100041, China
A Denavit-Hartenberg (D-H) quaternion transformation method for kinematics analysis of serial mechanisms was presented. Firstly, the point mapping is described with quaternion. Then a D-H quaternion transformations method for motion transformation between adjacent linkages was proposed. Moreover, the matrix operation method of D-H quaternion transformations was illustrated to construct the classical D-H homogeneous transformation matrix in robotics, which can be theoretically proven that the proposed D-H quaternion transformation method is correct. Based on the above D-H quaternion transformation formula of motion transformation between adjacent linkages, the D-H quaternion transformation method for kinematics analysis of serial mechanisms with any number of linkages was further proposed. By analyzing the kinematics of PUMA robot, the effectiveness and correctness of the proposed method was validated as well. The D-H quaternion transformation method has clear geometric meaning and the computation process is simple. The method is proved effective for kinematics analysis of serial mechanisms.
哈密顿于1843年创立了四元数[1-2],但四元数被发明后的一段时间内没有任何实际应用,而是作为四维线性代数的形式数学模式的范例[1].直到20世纪60年代以后,随着控制理论、计算机技术、刚体力学的发展,四元数开始在一些领域获得了应用. Denavit-Hartenberg(D-H)参数表示方法[3-4]能很方便地描述各杆件间的相对位姿,四元数能很方便地描述各杆件相对于固定参考系的空间几何关系,而且四元数方法较矩阵方法的优势是占用存储空间少、计算速度快[5].所提出的D-H四元数变换方法进行机构运动分析,充分发挥了D-H参数表示方法和四元数描述方法的双重优势,是除D-H齐次矩阵变换方法[6]外的一种新的机构运动学分析方法.而且,所提出的D-H四元数变换方法避免了复杂的矩阵运算,具有几何意义明确、计算简单的优势,是机器人机构运动分析的一种有效方法.
1 四元数的表示和运算方法四元数的定义,设
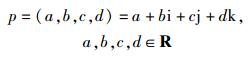
|
(1) |
其中i、j、k满足
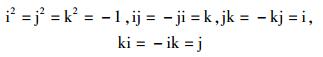
|
则称形式为式(1) 的数p为四元数,称a为四元数p的实部,称bi+cj+dk为四元数p的虚部.
下面以式(1) 四元数p为例,介绍四元数的坐标矩阵、分量矩阵和蜕变矩阵的表示方法.
四元数p的坐标矩阵为
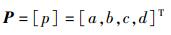
|
(2) |
四元数p的分量矩阵为
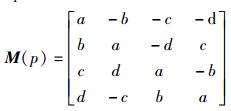
|
(3) |
四元数p的蜕变矩阵为

|
(4) |
四元数p、q、r有如下矩阵运算关系:
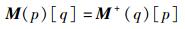
|
(5) |
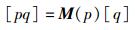
|
(6) |
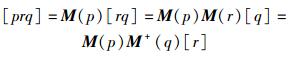
|
(7) |
空间中任一点P在不同坐标系中的描述是不同的,文献[6]介绍了点P从一个坐标系的描述到另一个坐标系的描述之间的映射关系,并用矢量和旋转矩阵表示了这种映射关系.下面介绍点P在不同坐标系中映射关系的四元数描述方法.
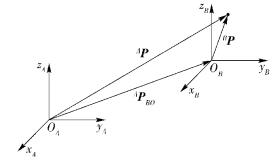
2.1 坐标系平移变换如图 1所示,原坐标系为{A},平移后的坐标系为{B}.平移矢量为APBO,用四元数表示为ApBO.点P在坐标系{A}中的位置为AP,用四元数表示为AP.点P在坐标系{B}中的位置为BP,用四元数表示为Bp.则点P在2个坐标系中的位置关系用四元数表示为
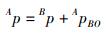
|
(8) |
|
图 1 坐标系平移变换 |
用四元数坐标矩阵表示为
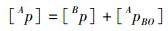
|
(9) |
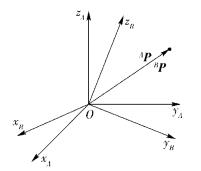
如图 2所示,坐标系{A}绕通过坐标原点的单位矢量e旋转θ角后形成坐标系{B}.设四元数
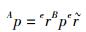
|
(10) |
|
图 2 坐标系旋转变换 |
用四元数坐标矩阵表示为
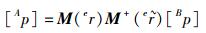
|
(11) |
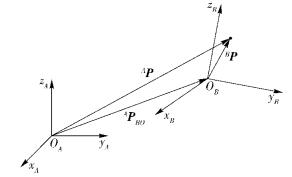
如图 3所示,坐标系{A}绕通过坐标原点的单位矢量e旋转θ角后,再相对于坐标系{A}平移且平移矢量为APBO,经过旋转和平移复合变换后形成坐标系{B}.则点P在2个坐标系中的位置关系表示为

|
(12) |
|
图 3 复合变换 |
用四元数坐标矩阵表示为
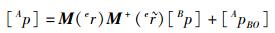
|
(13) |
下面将建立D-H四元数变换方法,给出D-H四元数变换的矩阵演算方法,由D-H四元数变换方法构造出机器人学中经典的D-H齐次矩阵,揭示D-H四元数变换方法与D-H齐次矩阵变换方法的内在联系,证明所提出的相邻连杆运动分析的D-H四元数变换方法与D-H齐次矩阵变换方法所得结果是一致的,验证所提出方法的正确性.
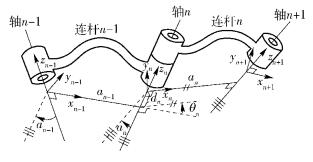
3.1 D-H连杆坐标系及其连杆参数D-H连杆坐标系的建立方法如图 4所示.坐标系{n}的z轴zn与关节轴n共线,指向任意;坐标系{n}的x轴xn与连杆公垂线重合,指向从关节n到关节n+1;坐标系{n}的y轴yn按右手法则确定;坐标系{n}的原点On取xn与zn的交点.
|
图 4 D-H连杆坐标系 |
连杆参数定义如下.
an-1:从zn-1到zn沿xn-1测量的距离;
αn-1:从zn-1到zn绕xn-1旋转的角度;
dn:从xn-1到xn沿zn测量的距离;
θn:从xn-1到xn绕zn旋转的角度.
3.2 相邻连杆运动分析的D-H四元数变换方法坐标系{n}相对于坐标系{n-1}的变换可依次通过如下步骤实现.
1) 绕xn-1轴转αn-1角;2) 沿xn-1轴移动an-1;3) 绕zn轴转θn角;4) 沿zn轴移动dn.
在坐标系{n}中的矢量nP,用四元数表示为np,依据坐标系{n}相对于坐标系{n-1}的变换步骤,np在坐标系{n-1}中用D-H四元数变换公式计算为
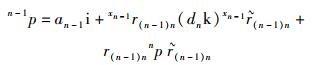
|
(14) |
式(14) 描述出了相邻连杆运动的坐标系变换的4个步骤,而且也描述出了点在不同坐标系中的位置变换关系,具有明确的几何意义.用1个公式描述出了2个坐标系的4步变换,通过简单的代数计算即可求出结果,避免了矩阵变换的复杂描述和计算.若用c表示余弦函数cos,用s表示正弦函数sin,式(14) 中的参数表示和计算为
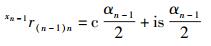
|
(15) |
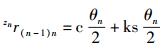
|
(16) |
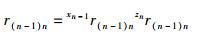
|
(17) |
则np在坐标系{n-1}中用D-H四元数变换公式计算为
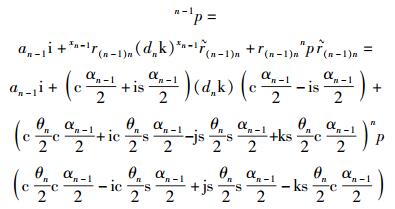
|
(18) |
D-H四元数变换的矩阵表示计算如下.写出式(14) D-H四元数变换公式的矩阵表示形式为
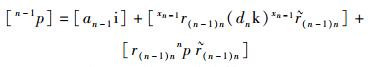
|
(19) |
式(19) 各项分别用矩阵演算为
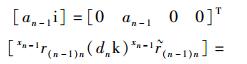
|
(20) |
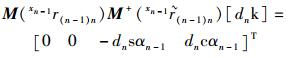
|
(21) |
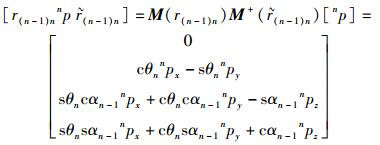
|
(22) |
则
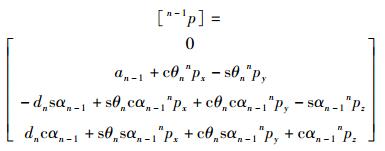
|
(23) |
下面采用D-H齐次矩阵变换方法计算坐标系{n}中的矢量nP在坐标系{n-1}中的表达式.直接采用文献[6]中D-H矩阵的计算结果,n-1P为
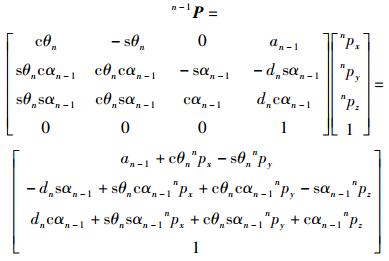
|
(24) |
式(23) 矩阵中元素0是四元数的实部为0,式(24) 矩阵中元素1是齐次坐标描述方法所增加的矩阵元素,与点的位置无关.从这2个矩阵中可以看出,点的位置表示完全相同,这就证明了所提出的机构运动分析的D-H四元数变换方法是正确的.
3.4 由D-H四元数变换方法构造出机器人学中经典的D-H齐次矩阵在机器人学中经典的D-H齐次矩阵[6]经常在机器人机构运动分析中采用,它的由来途径却很少被人关注.在3.3节中阐述了D-H四元数变换方法与D-H齐次矩阵变换方法所得结果是一致的,那么应该可以通过D-H四元数变换方法这种途径构造出D-H齐次矩阵. D-H齐次矩阵构造如下.
式(14) 前半部分
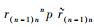
|
表示坐标系{n}的坐标原点相对参考坐标系{n-1}的平移变换,后半部分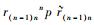
平移变换用矩阵演算为
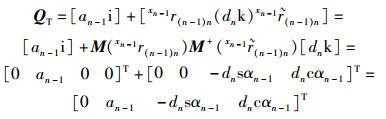
|
(25) |
旋转变换用矩阵演算为
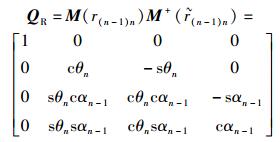
|
(26) |
由于四元数的实部和虚部的先后顺序不同但表示的四元数相同,所以可将平移和旋转矩阵改写为
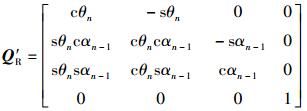
|
(28) |
将平移矩阵和旋转矩阵合并为1个矩阵表示为
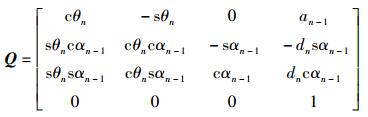
|
(29) |
以上通过所提出的D-H四元数变换方法构造出了D-H齐次矩阵,与机器人学中经典的D-H齐次矩阵相同.
4 任意个连杆的串联机构运动分析的D-H四元数变换方法将上述相邻连杆的D-H四元数变换方法进一步推广,坐标系{m}中矢量mP,用四元数表示为mp,在参考坐标系{0}中表示为0p,则机构运动分析的D-H四元数变换计算通式为
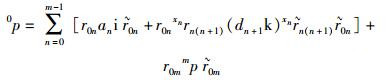
|
(30) |
其中
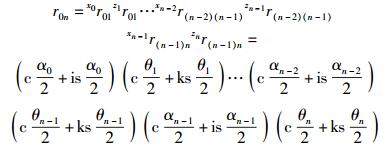
|
(31) |
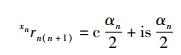
|
(32) |
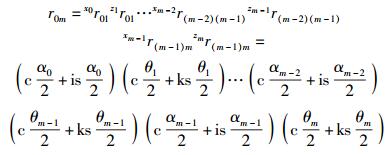
|
(33) |
分析式(30) D-H四元数变换通式可以看出,前半部分
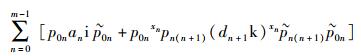
|
表示坐标系{m}的坐标原点相对参考坐标系{0}的平移变换,即描述坐标系{m}坐标原点相对于坐标系{0}的位置;后半部分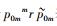
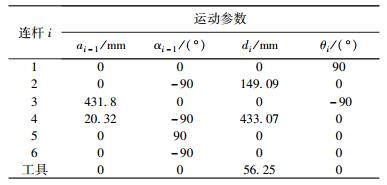
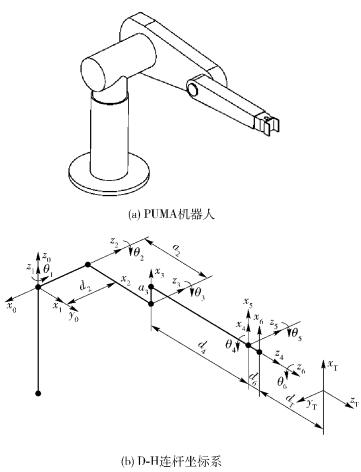
为了验证D-H四元数变换方法的有效性和正确性,以文献[6]中所给出的PUMA机器人为实例,对其进行运动分析. 图 5所示为PUMA机器人外形和D-H连杆坐标系及连杆参数,已知连杆参数值如表 1所示,并已知在末端坐标系中工具矢量6P,下面通过所提出的D-H四元数变换方法对这种机器人机构进行运动分析.
|
图 5 PUMA机器人和D-H连杆坐标系 |
|
|
表 1 PUMA机器人的连杆参数值 |
根据D-H四元数变换方法,坐标系{6}中矢量6P在参考坐标系{0}中的D-H四元数变换计算为
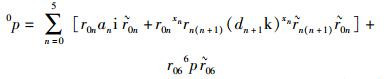
|
(34) |
经计算,得出四元数0p为
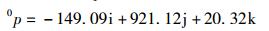
|
(35) |
式(35) 表示坐标系{6}中矢量6P在参考坐标系{0}中的位置,该位置矢量与通过文献[6]中给出的D-H矩阵计算结果完全一致,进一步验证了D-H四元数变换方法在机构运动分析中的正确性.
6 结束语提出了串联机构运动分析的一种新的方法,即D-H四元数变换方法. D-H四元数变换方法具有几何意义明确、计算简单的优势,是一种正确且有效的串联机构运动分析方法.给出了点的映射的四元数描述方法,并给出了相邻连杆间变换的D-H四元数变换方法和变换公式.建立了任意个连杆的串联机构运动分析的四元数变换通用公式,并建立了D-H四元数变换的矩阵演算方法.由所提出的D-H四元数变换方法构造出机器人学中经典的D-H齐次矩阵,揭示了D-H四元数变换方法与D-H齐次矩阵变换方法的内在联系,证明了所提出方法与D-H齐次矩阵变换方法在机构运动分析中所得结果的一致性.以PUMA机器人为实例,应用所提出的D-H四元数变换方法对其进行运动分析,验证了所提出方法的正确性和有效性.
| [1] | 勃拉涅茨B H, 什梅格列夫斯基И Π. 四元数在刚体定位问题中的应用[M]. 梁振和, 译. 北京: 国防工业出版社, 1977. |
| [2] |
程小红, 宋玉靖. 哈密尔顿与四元数[J]. 数学通讯, 2006(9): 47–48.
Cheng Xiaohong, Song Yujing. Hamilton and quaternions[J].Bulletin of Mathematics, 2006(9): 47–48. |
| [3] | Denavit J, Hartenberg R S. A kinematic notation for lower-pair mechanisms based on matrices[J].Journal of Applied Mechanics, 1995, 22(6): 215–221. |
| [4] | 李文亮. 四元数矩阵[M]. 长沙: 国防科技大学出版社, 2002. |
| [5] |
廖启征. 连杆机构运动学几何代数求解综述[J]. 北京邮电大学学报, 2010, 33(4): 1–11.
Liao Qizheng. Geometry algebra method for solving the kinematics of linkage mechanisms[J].Journal of Beijing University of Posts and Telecommunications, 2010, 33(4): 1–11. |
| [6] | 熊有伦, 丁汉, 刘恩沧. 机器人学[M]. 北京: 机械工业出版社, 1993. |