Yang等^[1]给出了模糊身份签名的概念.为了保证量子环境下的安全性，人们引入了基于格理论的密码体制^[2-3]. Yao等^[4]首次提出了基于格的模糊身份签名方案，但是它的安全性证明存在一些问题.笔者对这些问题进行了分析，给出了相应的改进方法, 并使用文献[3]中固定维数的格基代理技术，避免了文献[4]中格的维数扩展，构造了一个更高效的模糊身份签名方案.

1) 关于Extract Query，也就是私钥提取查询，文献[4]描述如下：给定id满足|id^*∩id| < k，查询E-列表寻找满足|id′∩id|≥k的id′.

① 如果(id′, (H₁(id′‖id_1′‖1), …, H₁(id′‖id_l′‖l)), (S′_{1, id1′}, …, S′_{l, idl′}))存在，返回S′_{1, id1′}, …, S′_{l, idl′}.

② 否则，执行对id的Hash查询. 在id-列表中寻找满足|id′∩id|≥k的id′.

a.如果id′存在，对所有的i∈[l]，计算S′_{i, idi′}←RandBasis(ExtBasis(S_{i, idi′}, A_{i, idi′}‖H₁(id′‖id_i′‖i)), s′)把(id′, (H₁(id′‖id_1′‖1), …, H₁(id′‖id_l′‖l)), (S′_{1, id1′}, …, S′_{l, idl′}))存在E-列表，把S′_{1, id1′}, …, S′_{l, idl′}返回给敌手

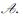
b.否则，对所有的i∈[l]，运行GenBasis(1ⁿ; 1^m; pq)算法产生矩阵 和格Λ_pq^⊥(W_{i, idi})的一个短基S_{i, idi}.然后，计算

把(id, (W_{1, id1}, …, W_{l, idl}))存在id-列表中，把(id, (W_{1, id1}, …, W_{l, idl}), (S′_{1, id1}, …, S′_{l, idl}))存在E-列表中，返回(S′_{1, id1}, …, S′_{l, idl})给敌手

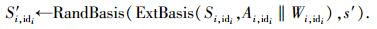
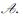
这里对id的私钥提取查询，除了步骤② 的b之外，返回的都是某个id′的私钥，二者具有关系|id∩id′|≥k.因此id和id′具有相同的私钥S′_{1, id1′}, …, S′_{l, idl′}.因此

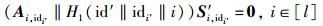
(1)

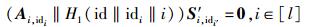
(2)

但A_{i, idi′}‖H₁(id′‖id_i′‖i)≠A_{i, idi}‖H₁(id‖id_i‖i)，在式(1) 成立的情况下，式(2) 是不成立的.即使是考虑id和id′相同的部分，也就是A_{i, idi′}=A_{i, idi}的时候，因为H₁(id′‖id_i′‖i)≠H₁(id‖id_i‖i) (若二者相同，则构成哈希函数的一个碰撞)，在式(1) 成立的情况下，式(2) 也是不成立的.

事实上，对id (满足|id^*∩id| < k)的私钥提取查询，不需要借助|id′∩id|≥k的id′，直接对id进行私钥提取查询即可.具体操作如下: 查询E-列表寻找id.

① 如果(id, (W_{1, id1}, …, W_{l, idl}), (S′_{1, id1}, …, S′_{l, idl}))存在于列表中，把(S′_{1, id1}, …, S′_{l, idl})返回给敌手

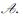
② 否则，执行对id的Hash查询. 在id-列表中寻找id.

a.如果(id, (W_{1, id1}, …, W_{l, idl}))存在id-列表中，对所有的i∈[l]，计算

把(id, (W_{1, id1}, …, W_{l, idl}), (S′_{1, id1}, …, S′_{l, idl}))存在E-列表中，返回(S′_{1, id1}, …, S′_{l, idl})给敌手

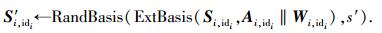
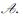
b.否则，对所有的i∈[l]，运行GenBasis(1ⁿ; 1^m; pq)算法产生矩阵和格Λ_pq^⊥(W_{i, idi})的一个短基S_{i, idi}.然后，计算S′_{i, idi}←RandBasis(ExtBasis(S_{i, idi}, A_{i, idi}‖W_{i, idi}), s′). 把(id, (W_{1, id1}, …, W_{l, idl}))存在id－列表中，把(id, (W_{1, id1}, …, W_{l, idl}), (S′_{1, id1}, …, S′_{l, idl}))存在E-列表中，返回(S′_{1, id1}, …, S′_{l, idl})给敌手

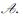
2) 关于Sign Query，也就是签名查询，在文献[4]中，因为与id^*满足|id^*∩id|≥k的id不允许进行私钥提取查询，所以与id^*满足|id^*∩id|≥k的id不可能在E－列表中，因此无法进行签名操作.

在对id^*与某个消息M进行签名查询时，需要先随机选取一个身份id，使之满足|id^*∩id|≥k，然后执行如下操作：

① 如果(id, (W_{1, id1}, …, W_{l, idl}))存在于id-列表中，对所有的i∈[l]，计算

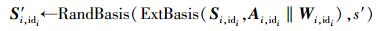
然后，运行算法Fuzzy. Sign((S′_{i, idi})_i∈[l], M))获得签名σ_{id, M}=(M, (e₁, …, e_l), id)并返回.

② 如果(id, (W_{1, id1}, …, W_{l, idl}))不存在id-列表中，对所有的i∈[l]，运行GenBasis(1ⁿ; 1^m; pq)算法产生矩阵和格Λ_pq^⊥(W_{i, idi})的一个短基S_{i, idi}，把(id, (W_{1, id1}, …, W_{l, idl}))存在id－列表中.然后，计算

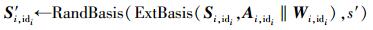
运行算法Fuzzy. Sign((S′_{i, idi})_i∈[l], M)获得签名σ_{id, M}=(M, (e₁, …, e_l), id)并返回.

这里只列出与原方案不同的设置.

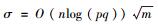
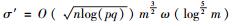
1) 参数s和s′被ω(log²m)和取代.

2)D_m×m.

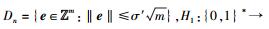
输入主私钥MK={T_{i, b}}_{i∈[l], b∈{0, 1}}，身份串id=(id₁, …, id_l)∈{0, 1}^l，执行以下操作：

1) 对i∈[l]，令

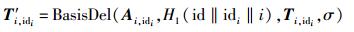
2) 输出id的私钥为sk_id=(T′_{1, id1}, …, T′_{l, idl}).

输入身份id及其私钥sk_id=(T′_{1, id1}, …, T′_{l, idl})和消息M，执行以下操作:

1) 令u=H₂(M).

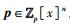
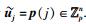
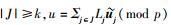
2) 随机选择一个最高次数为k－1的多项式向量，且p满足等式p(0)=u.对j=1, …, l，令.由Shamir的(k, l)门限方案，对J⊆[l]满足，这里的L_j是相应的拉格朗日系数.

3) 对i∈[l]，计算

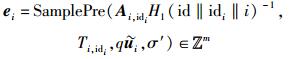
4) 输出签名σ_{id, M}=(M, (e₁, …, e_l), id).

输入身份id′、消息M和签名σ_{id, M}，

1) 令J⊆[l]表示id′和id相匹配位数的集合.如果|J| < k，输出⊥并终止；否则，执行下列步骤.

2) 验证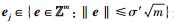是否对所有的j∈[l]都成立.如果不都成立，输出⊥并终止.

3) Σ_j∈JL_j(A_{j, idj}H₁(id‖id_j‖j)^－1)e_j=qH₂(M)(mod p)如果成立，验证通过；否则，输出⊥并终止.

对所有的i∈[l]，因为

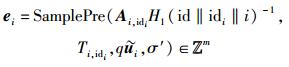
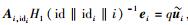
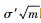
所以，并且‖e_i‖≤以很大的概率成立.

又由Shair的(k, l)门限方案，对J⊆[l]满足|J|≥k，，因此

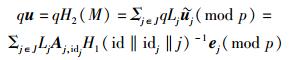
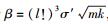
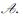
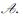
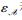
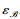
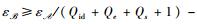
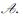
定理1 令，如果SIS_{n, 2ml, q, β}问题是难解的，则新方案具有自适应选择消息和身份攻击下的存在不可伪造性.换句话说，令是一个PPT敌手，则存在一个PPT算法可以解决SIS_{n, 2ml, q, β}问题，且和的成功概率和之间具有如下关系：negl(n)，这里的Q_id、Q_e、Q_s是敌手的H₁查询，私钥提取和签名查询的次数.

证明 令A=U₁‖X₁‖…‖U_l‖X_l.算法首先设置系统参数，操作如下：

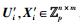
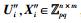
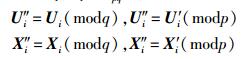
1) 对i∈[l]，随机选取，运用中国剩余定理计算，使之满足

2) 对i∈[l]，随机抽取矩阵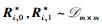，令A_i,0=U″_iR_i,0^*,A_i,1=X″_iR_i,1^*.

3) 随机选取J₀←{1, 2, …, Q_id+Q_e+Q_s+1}.

4) 输出主公钥{A_{i, b}}_{i∈[l], b∈{0, 1}}.

H₁查询 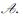询问H₁(id)时，算法如下操作：

1) 如果id已经被查询过，直接返回之前查询结果.

2) 如果是第J₀次查询，对i∈[l]，如果id_i=0，返回H₁(id‖id_i‖i)=R_{i, 0}^*；如果id_i=1，返回H₁(id‖id_i‖i)=R_{i, 1}^*；否则，执行步骤3.

3) 对i∈[l]，调用算法SampleRwithBasis(A_{i, idi})，输出矩阵R_{i, idi}和格Λ_pq^⊥(A_{i, idi}R_{i, idi}^－1)的一个短基S_{i, idi}.把(id, (R_{i, idi})_i∈[l], (S_{i, idi})_i∈[l])保存在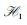列表中，返回(H₁(id‖id_i‖i)=R_{i, idi})_i∈[l].

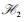
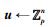
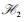
H₂查询 如果(M, H₂(M))在列表中，直接返回H₂(M).否则，随机选取，令H₂(M)=u，将(M, u)存入列表，并返回u.

私钥提取查询 当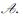询问身份id的私钥时，

1) 如果|id∩id′|≥k，拒绝应答.

2) 如果|id∩id^*| < k，查询列表对身份id的查询结果(id, (R_{i, idi})_i∈[l], (S_{i, idi})_i∈[l])，返回(S_{i, idi})_i∈[l].如果身份id不在列表中，先对身份id执行查询.

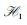
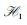
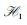
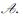
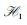
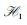
签名查询 当询问对身份id和消息M的签名时，算法执行如下操作：随机选取id′满足|id∩id′|≥k，查询列表寻找身份id′.如果(id′, (R_{i, idi′})_i∈[l], (S_{i, idi′})_i∈[l])存在，提取id′的私钥(S_{i, idi′})_i∈[l]，运行2.3签名过程对消息M签名得(M, (e₁, e₂, …, e_l), id′)并返回.如果身份id′不存在列表中，先对身份id′执行H₁查询.

伪造输出 当敌手输出一个合法的伪造(M*, (e1*, …, el*), id*)时，则对所有的i∈[l]，ei*∈Dn，并且存在一个子集J⊆[l]，|J|=k，满足Σj∈JLj(Aj, idj*Rj, idj**－1)ej*=qH2(M).

不失一般性，假设J={1, 2, …, k}，令D=(l!)².对j∈J，算法执行如下操作：如果id_j^*=0，e_j^**=[e_j^*; 0_m×1]；如果id_j^*=1，e_j^**=[0_m×1; e_j^*].则e^**=[DL₁e₁^**; …; DL_ke_k^**; 0; …; 0]是SIS_{n, 2ml, q, β}问题的解.分析如下：

① 猜对id*是第J0个H1查询的概率是1/(Qid+Qe+Qs+1).如果猜对了，而且(M*, (e1*, …, el*), id*)是一个合法的伪造，则ei*∈Dn，并且Σj∈JLj(Aj, idj*Rj, idj**－1)ej*=qH2(M).等式两边关于q取模，对j∈J，当idj*=0时，LjUjej=*0(mod q)；当idj*=1时，LjXjej*=0(mod q).又已知idj*=0时，ej**=[ej*; 0m×1]；idj*=1时，ej**=[0m×1; ej*].所以对j∈J，有Lj(Uj‖Xj)ej**=0(mod q).也就是(U1‖X1‖…‖Ul‖Xl)[L1e1**; …; Lkek**; 0; …; 0]=0(mod q)，亦即A[DL1e1**; …; DLkek**; 0; …; 0]=0(mod q).

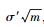
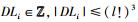
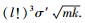
② 因为对所有的i∈[l]，有‖e_i^**‖=‖e_i^*‖≤，并且，，所以‖e^**‖≤

③ 因为H₂的结果服从均匀分布，H₂(M)=0的概率是可以忽略的，所以e^**=0的概率是可以忽略的.

综上所述，e^**是SIS_{n, 2ml, q, β}问题的解，并且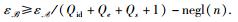

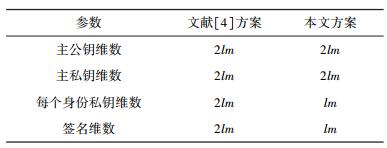
新方案采用了与文献[4]不同的格基代理技术，避免了格维数的扩展，使每个身份对应的私钥维数和签名维数变为原来的1/2.参数如表 1所示.

表 1

表 1

表 1 不同方案的参数

表 1 不同方案的参数

分析了文献[4]格上模糊身份签名方案的安全性证明中存在的问题，并对其逐一进行了修正.引入文献[3]中固定维数的格基代理方法，避免了文献[4]中格维数的扩展，构造了一个私钥维数和签名维数更短的签名方案，并对其安全性作了严格的证明.