研究了中频模拟器中时变系统采样间隔的高动态多普勒频移模拟方法.基于卫星运动模型研究了信号高动态频移特性, 提出基于变频率动态采样的伪码和载波多普勒频率偏移模拟方法; 给出高精度码多普勒频移模拟设计方案, 通过省略传统方法中必需的码数控振荡器模块来降低系统实现的硬件复杂度; 通过对伪码频率模拟误差精度的分析, 推导了算法主要参数取值的闭式解.仿真结果表明, 在接收信号频率具有有限二阶变化率的高动态环境下, 该方法可有效提升多普勒频移模拟精度, 并给出具有高稳定度的结果.
A method of high dynamic Doppler shift simulation with time-varying sampling interval on intermediate frequency simulator was presented. Based on satellite movement model, the high dynamic frequency shift characteristic of the signal was researched and a Pseudo-code and carrier Doppler shift simulated method was proposed as well based on variable frequency dynamic samplings. A design scheme of high-precision Doppler simulation was given, it reduces the system hardware complexity by omitting the code numerically controlled oscillator module in conventional methods. With analysis on error accuracy of pseudo-code frequency, the closed-form solution of the main parameters was derived. Simulation shows that the method can effectively improve the accuracy of the Doppler shift simulation, and provide high stability under high dynamic environment, with which, the frequency of the received signal will reach a finite second-order change rate.
高动态卫星信号模拟器可根据运动状态精确模拟载荷接收信号特性,多被用来评估接收机的捕获跟踪和动态性能,长期以来一直是相关领域的研究热点[1].在现有卫星信号模拟器中,卫星信号的多普勒特性被归结为动态伪码偏移和载波相位偏移[2],因而一般通过码数控振荡器(NCO, numerically controlled oscillator)和载波NCO实现扩频伪码信号的生成和载波信号的调制,进而实现对多普勒特性的精确模拟[3].其中,码NCO相位抖动是影响模拟器精度的一个重要因素[4].对于码NCO而言,输出的码信号相位存在过大的抖动会导致系统在某些时刻采样出错,从而严重影响多普勒动态模拟的精度[5].
针对上述问题,在全相参多普勒模拟算法的基础上,笔者提出了一种基于频率动态采样的多普勒信号生成方法,通过采样速率动态调整过程,实现多普勒特性的实时中频模拟,进而给出了基于该方法的中频信号模拟器硬件结构设计.仿真结果表明,在接收信号频率具有有限二阶变化率的高动态环境下,该方法可有效提高信号多普勒特性的模拟精度,且结果具有高稳定度.
1 信号多普勒特性模拟方法原理1.1 全相参多普勒频移模拟算法[1, 3]卫星与接收机之间的高速相对运动会导致接收机收到的卫星信号存在多普勒频偏,其影响主要体现在调制数据的扩频伪码和载波中.通过相邻采样时刻伪码和载波的相位关系,将多普勒频偏模拟出来即为全相参多普勒模拟算法.以下结合运动模型阐述该算法的基本原理.
设接收机相对于卫星做朝向卫星飞行的径向变速运动,该运动模型可以描述为
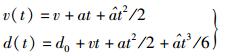
|
(1) |
其中:v(t)为实时径向速度,d(t)为径向运动位移,d0为初始位移,v、a、
在实际应用中,为了方便对接收机的测试和检验,通常会省略对接收射频信号进行下变频的过程,因此要求模拟器可以根据实际需要模拟中频信号.设发射信号的射频频率为fR,系统下变频采用的本振频率为fr,则模拟器所模拟的卫星中频信号频率为fC=fR-fr.若接收机与卫星的初始径向距离为R,多普勒频偏时延为τd,参照式(1) 提出的运动轨迹,根据系统时延τ=R/c+τd=[R-v(t)t]/c(c为光速)可以得到中频信号表达式为(只考虑多普勒频偏误差)
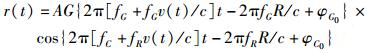
|
(2) |
其中:A为信号幅度,G为扩频伪码,φG0和φC0分别为伪码和载波初始相位,fG为伪码速率.
模拟器的数字信号处理部分需要对模拟信号进行采样,设系统单位采样时间间隔为Ts,则可以得出t=(n+1)Ts时刻相对于nTs时刻的伪码相位增量和载波相位增量分别为
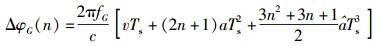
|
(3) |

|
(4) |
由式(3) 和式(4) 算出每个采样时刻对应的伪码和载波相位增量,叠加到相应时刻伪码和载波的实际值上,即可得到下一采样时刻的伪码和载波相位.当系统采样速率满足奈奎斯特采样定律时,在误差允许范围内,伪码多普勒频移fdG(n)和载波多普勒频移fdC(n)与其相位增量满足下列关系:
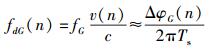
|
(5) |
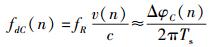
|
(6) |
其中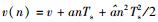
由上述推导可见,利用相邻采样时刻伪码和载波的相位差可以对多普勒频偏进行模拟,这就是全相参多普勒频移模拟算法的核心原理.
1.2 基于变频率动态采样的多普勒模拟方法全相参多普勒模拟算法通过计算相邻采样时间伪码和载波的相位差对扩频码和载波信号的相位进行控制,其相位的输出时刻与采样时钟有关.若采样点间隔大小不变,接收机和卫星之间做相对匀速运动,则相邻采样时刻的相位差保持不变;若做相对加速运动,则相位差逐渐增加.假设相邻采样点间的相位增量为一固定常数,通过改变采样点间隔可使伪码和载波的相位的变化呈现变速运动的特性.基于该原理,提出了一种变频率动态采样多普勒模拟方法,通过改变码相位和载波相位与采样时钟间隔之间的关系来模拟信号的伪码和载波多普勒频偏变化.其原理如下.
假设固定采样间隔Ts与初始伪码频率fG间存在关系:
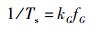
|
(7) |
其中kG为初始采样时钟相对于伪码码片的采样率(采样个数),其值为一固定整数.那么通过式(5) 的结论可以计算出实际接收到的伪码频率frG(n)为

|
(8) |
由式(8) 可以看出,接收到的伪码频率可以由伪码相位和固定的采样时钟间隔大小计算得出.若保持伪码相位为2π不变,则变加速运动的模拟可通过改变采样间隔的方式实现.假设固定伪码相位增量为0,由伪码频率计算出的采样时钟间隔为
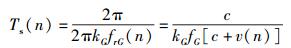
|
(9) |
由式(9) 可见,采样时钟间隔随运动速度而发生变化.此时只需按照kG对伪码进行动态采样,即可保证输出受到多普勒影响的伪码的变化规律与全相参模拟算法一致.由于该方法不需码NCO的参与,所以在具体应用时不仅节省了传统算法中相应的硬件资源,而且消除了码NCO相位抖动对模拟器精度的影响.
对于中频载波来说,由于和伪码共用同一个采样时钟,所以当载波相位保持不变时,会产生一个新的载波频偏.设中频频率为fC时,采样时钟Ts相对fC的采样率为kC,那么伪码频率和中频载波频率及其采样率之间存在固定关系kGfG=kCfC.在变频率时钟采样条件下,接收到的中频载波频率可以写为
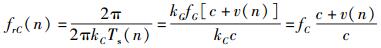
|
(10) |
于是可以推出载波频偏fΔC(n)为
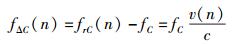
|
(11) |
由前文描述可知,模拟器产生的中频载波频率是为了方便测试接收机性能而计算得出的,实际上发射信号的载波多普勒频偏与发射射频频率fR有关.由式(6) 和式(11) 可以看出,变频率采样后的中频载波频偏和理论上应接收到的载波频偏之间有明显差异,所以模拟器需要产生一个频率为ΔfC的补偿载波使得载波频率可以达到fdC(n).该补偿频率为
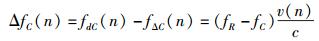
|
(12) |
根据上述推导,利用相位增量和采样间隔之间的关系可以对多普勒频偏进行模拟.利用伪码相位增量和速度计算出采样时钟间隔的大小,然后按照kG对伪码进行动态采样以模拟伪码多普勒频偏.载波多普勒模拟的原理与伪码模拟相同,但由于实际的载波频偏由射频频率决定,而中频受到多普勒影响无法达到真实频偏值,因此需要对中频载波的频偏进行补偿.该过程可以利用载波NCO实现,NCO输出频率值可由式(12) 计算得出.
该方法与全相参模拟算法最大的区别在于保持相位增量不变而采样时钟可变,从而保证了采样时钟频率始终保持为伪码速率的整数倍,避免了码NCO中存在的2个连续码片采样点数不一致的问题,减少了伪码相位抖动.
2 变频率动态采样中频模拟方法的硬件方案设计根据对基于变频率动态采样的多普勒模拟方法描述,给出了一种高动态卫星信号中频模拟器模型,可根据设定的信号特性模拟产生接收机中频信号及相应的采样数据.本节首先介绍模拟器的结构组成,随后给出实现变频率动态时钟并模拟伪码和载波多普勒频偏的具体方法.
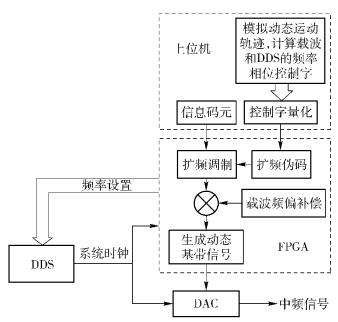
2.1 高动态中频模拟器结构为达到实现高动态多普勒中频模拟目的,信号模拟器主要由现场可编程门阵列(FPGA, field-programmable gate array)、上位机、直接数字式频率合成器(DDS, direct digital synthesizer)和数模转换器(DAC, digital to analog converter)组成[6],其主要结构如图 1所示.
|
图 1 模拟器结构框图 |
模拟器利用DDS产生一个系统时钟,同时把它作为DAC的输入时钟和FPGA的内部工作时钟,即前文所述的变频率采样时钟.上位机负责用户运动模型的建立和动态运动轨迹的模拟,并计算载波和DDS的频率相位控制字等.模拟器在DAC中实现基带信号到中频信号的调制过程,同时对信号进行数模变换以便完成射频发送. FPGA的主要功能是对发送数据进行扩频调制,通过载波NCO产生补偿载波对信号进行射频频偏调制,并对DDS进行配置来实现采样时钟的动态采样[7].
2.2 变频率采样时钟的产生和伪码输出根据1.2节中方法,模拟器不需要码NCO模块,只需在FPGA内部按照固定的采样个数对伪码模块接口进行读操作就可以生成动态伪码.因此,为了实现动态多普勒模拟,首先应产生变频率采样时钟.如图 1所示,模拟器利用外置的DDS芯片产生动态正弦波,进行方波变换后将其作为FPGA的系统时钟.为使DDS正常工作,需给芯片提供一个外部工作时钟,其频率设置为fs,大小为kGfG.模拟器通过FPGA对DDS芯片进行设置,其配置参数与芯片型号有关,可参照芯片手册实现,在此不加赘述.这里主要给出其中2项重要参数——时钟初始相位控制字和频率控制字的计算公式.
由于存在系统时延,接收机接收到的信号相位中会包含距离信息,所以模拟器所模拟的信号中需要存在一个由时延造成的初始相位,该初始相位可以通过采样时钟的初始相位加以体现.以变加速直线运动为例,n=0时刻采样时钟的初始相位为
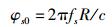
|
(13) |
DDS的相位初值应为初始相位的小数部分,即

|
(14) |
其中:N(0) 为完整采样间隔的个数,P为DDS初始相位控制字位宽.
当fs足够大即时钟间隔T=1/fs足够小时,相邻采样时刻的运动距离差与速度之间存在如下关系:
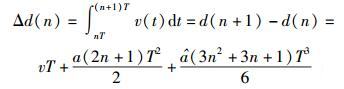
|
(15) |
因此每个采样时刻的实时速度可以近似为
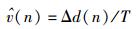
|
(16) |
利用式(15) 和式(16) 可以直接在运动模型中提取每一采样时刻的距离,根据相邻采样时刻的距离差计算出速度,从而降低多普勒模拟算法实现的复杂度.将式(15) 和式(16) 代入式(9) 并取倒数即可得到采样时钟频率为
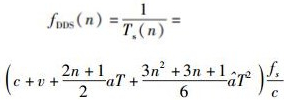
|
(17) |
其频率控制字为
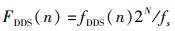
|
(18) |
其中N为DDS频率控制字位宽.
DDS在每个外部工作时钟(频率为fs)周期进行一次频率控制字更新,更新值可以由式(18) 计算得出.由此可以得到一个时变的采样时钟.
产生采样时钟后,FPGA可以利用采样频率和伪码速率之间的固定关系来输出伪码.由于采样率kG=fs/fG为整数,首先将扩频码序列存储在FPGA内部,设置一个采样时钟计数器,每计数kG个后按序对扩频码序列进行读取,再与发送的数据进行异或运算,就可以得到要发送的伪码序列.
2.3 基于NCO的中频载波设计模拟器需要通过FGPA和DAC两部分来实现中频输出,其中DAC芯片负责将基带信号直接调制到中频,FGPA负责对DAC进行参数配置以及产生式(12) 所描述的补偿载波.
DAC以DDS输出的变频率采样时钟作为芯片工作时钟.由于采样时钟的初始相位也会对DAC造成影响,所以DAC的初始相位为0.而DAC输出的中频载波频率为fC=fR- fr,其中fR为发送射频频率,fr为接收端下变频本振频率,由此可以计算出DAC芯片的频率控制字为
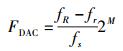
|
(19) |
其中M为DAC频率控制字位长.
FPGA对DAC只在系统上电初始化时进行一次配置,之后便不再更改.但是由于DDS输出的采样时钟是时变的,DAC输出的中频信号的频率会因为受到动态采样的影响而存在一个频偏,其大小在式(12) 中给出.此时则需要在FPGA内部建立一个载波NCO,并产生相应载波,对基带信号进行射频频偏调制,即对中频载波进行补偿.
载波NCO是基于DDS的数字载波结构原理来生成数字载波. NCO产生的载波频率大小为式(10) 的计算结果,其值也随采样时钟而变化,因此需要在时钟到来时刻不断更新频率控制字F(n).频率控制字的计算方法为
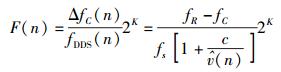
|
(20) |
其中K为相位累加器位宽.代入式(15) 和式(16) 的结果可得频率控制字的最终结果为
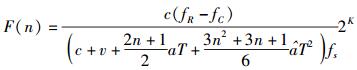
|
(21) |
如前文所述,采样时钟包含了初始距离信息,因此初始相位为0.将此相位值设为相位累加器的初值,在每个采样时刻对更新的频率控制字进行累加. FPGA内部ROM中存储了一个完整的SINE查找表,因此对相位累加器高位值的读取就可以实现相位到正弦幅值的映射,从而输出一个频率为ΔfC(n)的正弦波作为对中频载波的补偿.
3 系统仿真结果为验证新方法的性能,在高动态环境下进行了仿真验证.设动态环境:初速度为100 m/s,加速度为10 m/s2,急动度为3 m/s3,某卫星信号码速率为8.184 Mchip/s,初始采样频率为81.84 MHz,模拟器输出中频频率为60 MHz,在此条件下将变频率动态采样方法与利用码NCO和载波NCO的全相参算法进行仿真对比. 图 2和图 3分别给出了2种方法下多普勒模拟频偏值与理论值之间的误差.
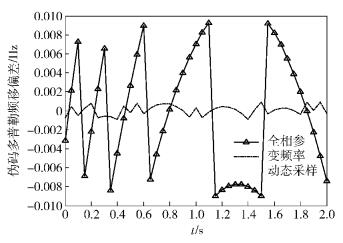
|
图 2 伪码多普勒频移仿真误差 |
由图 2和图 3的仿真结果可见,在频率控制字计算过程中,量化取整会导致仿真误差的突变.从图 2可见,利用DDS产生变频率采样时钟模拟伪码频偏的方法,其误差稳定在±0.002 Hz内,远远小于采用码NCO模拟伪码频率多普勒的传统全相参方法;图 3显示的动态采样算法中频载波补偿与全相参载波NCO直接生成中频载波的仿真误差没有明显差别.于是对2种算法在不同急动度下仿真误差的均值和标准差做了进一步分析,结果如图 4所示.

|
图 3 载波多普勒频偏误差 |
图 4表明,当急动度在0~50 m/s3之间变化时,2种方法的仿真误差均值一致,其绝对值保持在0.005 Hz以内.但是变频率动态采样方法可将仿真误差结果的标准差控制在0.01 Hz内,明显优于全相参载波NCO.这说明在动态载波模拟方面,笔者提出的方法比全相参算法要更加精确稳定.
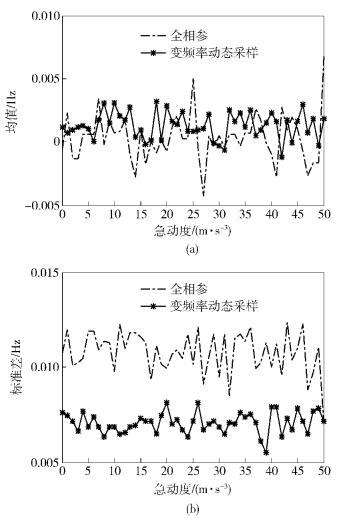
|
图 4 载波多普勒频偏仿真误差的均值和标准差 |
通过研究卫星运动模型信号的高动态频移特性,在全相参多普勒频移算法的基础上,提出了基于变频率动态采样的伪码和载波多普勒频率偏移模拟方法;设计了高精度码多普勒频移模拟硬件方案,其中省略了码NCO模块使得系统实现的硬件复杂度得到了一定改善;通过分析伪码频率误差精度,推导出了算法主要参数取值的闭式解.最后给出了算法的仿真结果,并与全相参多普勒频移算法进行了对比,结果表明,在接收信号频率具有有限急动度即二阶变化率高的动态环境下,该方法在多普勒频移模拟精度和稳定度上具有明显优势.
| [1] |
齐巍, 常青, 张其善, 等. 高动态信号模拟器中的多普勒模拟算法[J]. 航空学报, 2008, 29(5): 1252–1257.
Qi Wei, Chang Qing, Zhang Qishan, et al. Arithmetic of Doppler simulation in high dynamic signal simulator[J].Acta Aeronautica et Astronautica Sinica, 2008, 29(5): 1252–1257. |
| [2] |
侯博, 谢杰, 刘光斌. 卫星信号模拟器的发展现状与趋势[J]. 电讯技术, 2011, 51(5): 127–132.
Hou Bo, Xie Jie, Liu Guangbin. Navigation satellite signal simulator: current status and developing trend[J].Telecommunication Technology, 2011, 51(5): 127–132. |
| [3] | Dong Lei. IF GPS signal simulator development and verification[D]. Calgary: University of Calgary, 2003. |
| [4] |
孟繁智. 高动态GPS卫星信号模拟源的关键技术研究[D]. 长沙: 国防科学技术大学, 2004.
Meng Fanzhi. The research of the key technologies in the high dynamic GPS satellite signal simulator[D]. Changsha: National University of Defense Technology, 2004. |
| [5] |
章小梅, 姜茂仁, 费元春. DDS杂散的抑制与仿真研究[J]. 信息技术, 2006, 30(4): 1–3.
Zhang Xiaomei, Jiang Maoren, Fei Yuanchun. Simulation research and spurious reduction of DDS[J].Information Technology, 2006, 30(4): 1–3. |
| [6] |
石阳, 刘光斌. 基于FPGA技术的GPS卫星数字中频信号模拟器设计[J]. 航天控制, 2008, 25(6): 75–77.
Shi Yang, Liu Guangbin. A digital GPS signal simulator based on FPGA technology[J].Aerospace Control, 2008, 25(6): 75–77. |
| [7] |
任风华, 符强, 纪元法, 等. GPS模拟器的FPGA实现及其杂散研究[J]. 计算机测量与控制, 2013, 21(8): 2224–2226, 2273.
Ren Fenghua, Fu Qiang, Ji Yuanfa, et al. Study on generation of GPS simulator IF signal using FPGA with consideration of spurious error[J].Computer Measurement and Control, 2013, 21(8): 2224–2226, 2273. |


