在数字通信领域中，当给定系统为所允许的带宽和平均功率时，星座图的设计有2个主要目标：一是最大化最小欧氏距离，二是降低调制信号的峰均比.为了同时优化这2个方面的性能，有学者提出了正六边形星座调制信号(HSC, hexagonal signal constellation)的概念^[1-4]. HSC不仅具有与标准正交幅度调制类似的欧氏距离性能，而且同时保持了与相移键控调制接近的低峰均比的良好特性，因此近年来HSC得到了深入的研究，并被应用在多输入、多输出和光学通信系统领域^[5-6].

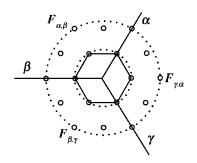
现有HSC解调算法的运算复杂度，一般都与星座点数成线性增大的关系.文献[4]提出的基向量投影(BVP, base vector projection)解调算法的运算复杂度不随星座点数而改变，在大星座的解调过程中极具优势，并且在高信噪比的条件下，BVP解调算法可以进一步优化.在上述背景下，笔者提出了一种基于非正交矢量投影的HSC低复杂度解调算法.

图 1为极坐标下3阶HSC图，圆点表示可用的信号星座点，与坐标原点距离相同的星座点在同一阶上.设定基矢量α=e^jπ/3, β=e^jπ, γ=e^-jπ/3；α、β、γ之间的区域分别表征为F_{α, β}、F_{β, γ}、F_{γ, α}；为保持区域表征的完整性和连续性，设定α∈F_{α, β}，β∈F_{β, γ}，γ∈F_{γ, α}.

图 1

图 1

图 1 极坐标下的典型HSC星座图

对于任意矢量V可表示为

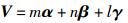
(1)

其中：m、n和l为矢量V分别在基矢量α、β、γ上的投影系数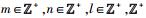，表示非负整数集.

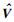
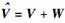
基于典型HSC模型，文献[4]提出了BVP解调算法，解调过程即为求解任意矢量在基矢量上的投影系数m、n和l.假设为叠加了加性高斯白噪声的接收矢量，表示为，其中W是均值为零、方差为σ²的高斯白噪声.

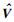
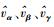
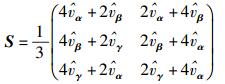
BVP解调算法首先计算了矢量与3个基矢量的内积；然后将3个内积结果按一定方式组成一个3×2的矩阵；再与转换矩阵T相乘，最终得到系数矩阵S：

(2)

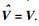
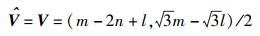
在无噪声情况下，W=0，则有为了计算的方便直观，将极坐标系转换为直角坐标系. 3个基矢量在直角坐标系下的坐标表示分别为α=(1/2, 3/2)，β=(－1, 0)，γ=(1/2, －3/2)，则

(3)

其中：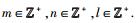

计算出V与3个基矢量的内积的坐标表示，并代入式(2)，则无噪声情况下的系数矩阵S_no-noise为

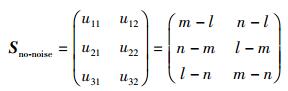
(4)

其中u₁₁~u₃₂为矢量V的投影系数.

观察可知，式(4) 中的系数矩阵S_no-noise每两行之间都存在一对互为相反的元素.假如矢量，且与α不同向，则必有投影系数，l=0，其中为自然数集.故S_no-noise第1行的所有元素都为正数，第2行u₂₂和第3行u₃₁一定是负数.对于，同理适用.因此，BVP算法根据系数矩阵S_no-noise的某行元素是否都为正数，判定矢量的所属区域，同时得到相应的投影系数.

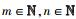
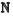
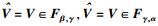
在有噪情况下，，此时系数矩阵S_noise为

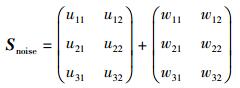
(5)

其中w₁₁~w₃₂为噪声W的投影系数.

式(5) 矩阵S_noise中的元素并不一定是整数.在这种情况下，应该先将矩阵S_noise中的每个元素四舍五入取整，然后再按照上述规则进行判决和映射.

假设为接收到的矢量，在高信噪比的条件下，基于非正交矢量投影的HSC低复杂度解调算法的实现步骤分为以下5步.

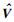
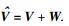
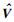
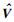
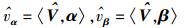
第1步 计算接收矢量与3个基矢量的内积.

矢量与α、β的内积分别为

(6)

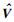
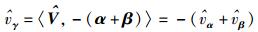
根据矢量运算的平行四边形法则，矢量与γ的内积为

(7)

第2步 取内积结果符号.

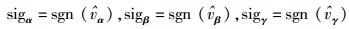
(8)

其中符号函数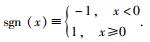

第3步 定义域判决.

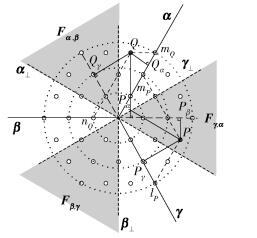
图 2为极坐标下5阶HSC星座图.其中，α_⊥、β_⊥、γ_⊥分别为基矢量α、β、γ的垂直矢量；P和Q为星座点；P_α、P_β、P_γ和Q_α、Q_β、Q_γ分别为星座点P和Q在基矢量α、β、γ上的正投影点；m_P、l_P、m_Q分别为极坐标系下星座点P和Q在基矢量α、β、γ上的投影系数.

图 2

图 2

图 2 5阶HSC星座图

在直角坐标系中，信号矢量与基矢量内积结果的正负与其在星座图中所处的位置有关.根据内积和正投影原理可知，若〈A, i〉=|A|cos θ，i为单位矢量，θ为A和i的夹角，则A与i的内积等于A在i上的正投影.由此推出信号矢量与基矢量的内积结果分为以下3种情况.

1) 星座点落在图 2阴影区中及阴影边界上，如P点，信号矢量P∈F_{γ, α}，P点正投影在基矢量α、γ的正半轴上，正投影在基矢量β的负半轴上，即〈P, α〉、〈P, γ〉为非负数，〈P, β〉为负数.

2) 星座点落在图 2非阴影区中，如Q点，信号矢量Q∈F_{α, β}，Q点正投影在基矢量α的正半轴上，正投影在基矢量β、γ的负半轴上，即〈Q, α〉为正数，〈Q, β〉和〈Q, γ〉为负数，并且〈Q, β〉的绝对值小于〈Q, γ〉的绝对值.

3) 特殊情况下，对于和某个基矢量同方向的信号矢量，其与另外2个基向矢量的内积结果是2个大小相等的负数.需要注意的是，在有噪声情况下，2个负内积结果可能不相等，但两者相差不大.

综上可知，接收矢量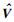与基矢量的内积结果会出现3种情况：2个正数和1个负数；1个正数和2个负数，其中1个负数的绝对值很小；1个正数和2个绝对值相等或者几乎相等的负数.

根据以上分析结果，判决规则和步骤如下：

1) 选择与接收矢量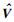内积结果为非负的基矢量及相应内积结果.

2) 如果第1) 步中选出了两组结果，则判决结束；如果第1) 步中只选出了一组结果，则进行第3) 步.

3) 比较剩下的2个负内积结果的绝对值大小.如果两者相差小于±d/8(d为最小欧氏距离，此值可根据具体情况设计)，判决结束；否则，进行第4) 步.

4) 选择绝对值较小的基矢量及其内积结果，判决结束.

第4步 计算投影系数.

在有噪声的情况下，系数矩阵满足S=S_noise，代入式(2) 和式(5)，并将等号左右同时乘3得

(9)

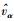
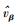
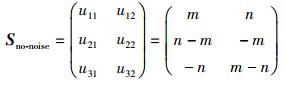
假设在第3步中α、β、和被选择，则有l=0.此时

(10)

令

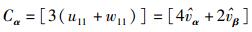
(11)

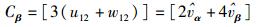
(12)

其中[x]表示实数x四舍五入运算.

如果系统的信噪比足够高，使得[3(u_ij+w_ij)]=3u_ij以接近于1的概率成立，则有

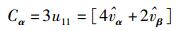
(13)

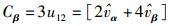
(14)

式(13) 和式(14) 计算出了投影系数u₁₁和u₁₂的3倍结果C_α和C_β.

第5步 恢复调制信号.

由于线性运算不会改变调制信号和星座点之间一一对应的关系，所以可预先将星座点在基矢量上的投影系数乘3，保存成一个映射表；然后根据第4步中计算出的系数C_α和C_β进行查找和映射，即可将接收的信号映射回原信息比特.

在第1步中，使用点乘法计算二维矢量内积，故1次内积需要2次实数乘法和1次加法，另外式(7) 需要1次实数加法，所以第1步中共需要4次实数乘法和3次实数加法；在第4步计算投影系数中，式(13) 和式(14) 中的乘法运算可以通过移位实现，所以计算2个投影系数只需要进行2次加法运算；第2步取符号和第3步判决定义域，以及第5步恢复调制信号，都不需要使用加法或者乘法进行运算.综上分析可知，基于非正交矢量投影的HSC低复杂度解调算法共需要4次实数乘法和5次实数加法.

对于任意矢量，传统HSC解调算法的运算复杂度随着星座点数增加而线性增大.虽然BVP解调算法的复杂度不会随着星座点数增加而线性变大，但其仍需要进行18次实数乘法和9次实数加法^[4].而基于非正交矢量投影的HSC低复杂度解调算法，其运算复杂度不会随着星座点数线性增加，且仅约为BVP解调算法运算复杂度的30%.

基于非正交矢量投影的HSC低复杂度解调算法正确运行的条件是信噪比达到一定的门限值，使得[3(u_ij+w_ij)]=3u_ij以接近1的概率成立.此处相当于[u_ij+w_ij]=u_ij以接近1的概率成立，即噪声分布在判决域内的概率很大.

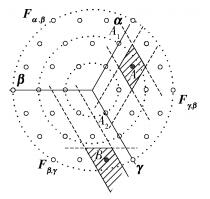
HSC是正六边形网格被圆形截取的一部分.以任一星座点为圆心做与边界圆相切的圆，其最小半径定义为星座点到边界的距离.定义到边界距离大于等于1的点为星座内点，到边界距离小于1的点为非内点，图 3中A为内点，B为非内点.

图 3

图 3

图 3 HSC内点和非内点判决域

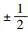
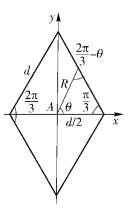
网格理论表明，网格点具有同等数量的邻点，并具有全等的判决域，内点仍保有网格点的特征.但是，对于靠近圆形边界的非内点，由于其邻点数量减少，判决域会发生改变.无噪声时，星座内点A在基矢量α上的投影为A₁，在基矢量γ上的投影为A₂；叠加噪声后，只要A在基矢量α和γ上的投影分别落在以点A₁和A₂为中心的的区间内，则A的投影系数经四舍五入后，其结果一定和无噪声时的投影系数相同.由此可得内点A的判决域是一个顶角为60°的封闭的菱形.而对于非内点B，由于其下端没有邻点，所以它的判决域是开放的.

通过上述分析可知，内点的判决域是封闭的、最小的.如果内点判决域内的噪声概率分布满足门限要求，则非内点的也一定满足.此外，在一定的星座阶数下，内点的数量最多，所占比例最大.因此，研究内点判决域内的噪声概率分布最具有代表意义. 图 4以星座内点A为坐标原点建立直角坐标系，R为坐标原点到菱形判决域边界的距离.

图 4

图 4

图 4 HSC内点和非内点判决域

若最小欧氏距离为d，则A的判决域边界可表示为

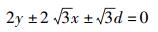
(15)

其中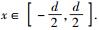下面将分析计算加性高斯白噪声在菱形判决域内的概率分布.

加性高斯白噪声的数学模型是零均值窄带平稳高斯随机过程，其幅度和相位的概率密度函数相互独立，其中幅度服从瑞利分布，相位服从[0, 2π]均匀分布，所以噪声幅相二维联合概率密度为

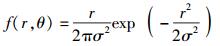
(16)

其中：r为幅度，θ为相位，σ²为噪声功率.

噪声在菱形判决域内的概率分布Λ，即接收矢量落在菱形判决域内的概率Λ为

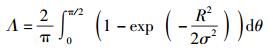
(17)

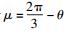
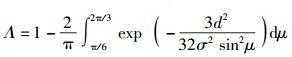
根据正弦定理，并令，可得

(18)

HSC信号功率为

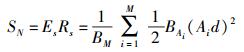
(19)

其中：E_s为每个符号的功率，R_s为符号速率，A_i为对d归一化后的星座点幅值，B_Ai为幅值A_i对应的点数.

由式(19) 可以推导出，对于不同点数的调制，信号功率S_N与最小欧氏距离d的二次方成比例，即

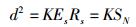
(20)

其中K为实数.对于不同点数的HSC调制，K取不同的值，保持信号功率不变，调制点数越多，K越小.而对于标准带通系统，噪声功率为

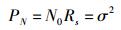
(21)

其中N₀为单边噪声功率密度.

对于标准带通系统，有

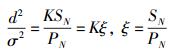
(22)

将式(22) 代入式(18) 得

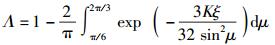
(23)

式(23) 表明，接收矢量落在菱形判决域内的概率分布Λ(K, ξ)和参数K、ξ有关，其中概率Λ(K, ξ)与K成正比，与ξ成反比.同时，根据式(20) 可得出参数K随着星座调制点数的增加而减小的结论，从而推导出概率Λ(K, ξ)与星座调制点数成反比.

式(23) 包含指数平方项，不是初等函数，难以得到传统意义上的解析表达式.基于高斯求积的数值分析方法是精度最高的插值型数值积分，计算量小，并且可以精确计算包含e^－x及e^－x2等因子的广义积分，非常适于计算上述公式^[7].使用变换式对式(23) 进行换元，则菱形判决域内的噪声概率分布为

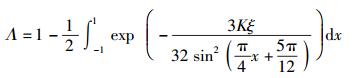
(24)

接下来采用4点高斯-勒让德求积公式进行数值计算：

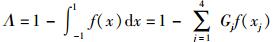
(25)

其中：

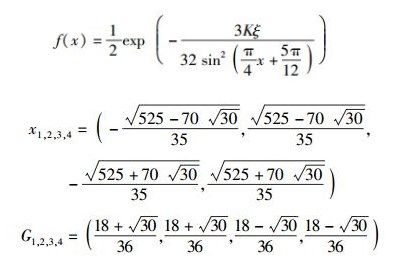
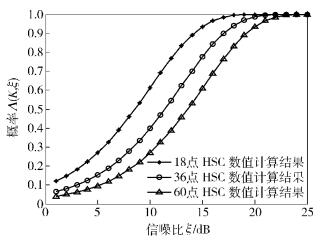
对不同星座点数(18点、36点和60点)下HSC调制的接收矢量落在菱形判决域内的概率Λ(K, ξ)与ξ的关系进行了研究，Matlab计算和仿真结果如图 5所示.

图 5

图 5

图 5 概率Λ(K, ξ)与信噪比ξ的关系

从图 5中可以看出：

1) 固定HSC星座调制的点数，随着K的增大，概率Λ(K, ξ)呈单调递增趋势；

2) 对于相同的ξ，随着HSC星座调制点数的增加，接收矢量落在判决域内的概率Λ(K, ξ)变小；

3) 随着HSC星座调制点数增加，对于达到概率Λ(K, ξ)所需信噪比门限变高.

表 1列出了18点、36点和60点的HSC星座调制，接收矢量落在判决域内的概率大于0.99时分别所需要的信噪比门限.

表 1

表 1

表 1 不同调制点数(Λ(K, ξ)≥0.99) 时的信噪比门限

表 1 不同调制点数(Λ(K, ξ)≥0.99) 时的信噪比门限

在传统HSC解调算法运算复杂度较高的背景下，提出了一种基于非正交矢量投影的HSC低复杂度解调算法.采用投影法推导出极坐标下HSC信号矢量的投影系数，并结合高斯-勒让德数值分析方法计算出本算法有效运行的信噪比门限.结果表明，信噪比超过门限时，基于非正交矢量投影的HSC低复杂度解调算法有效运行，并且运算复杂度仅约为BVP算法的30%.