2. 北京邮电大学 信息光子学与光通信研究院, 北京 100876
电力系统缺少明确的电力通信系统可靠性定义和定量的测度判据, 仅用通信通道中断衡量通信网的可靠性不科学, 不能客观反映通信网的真实运行情况.前人的研究并没有考虑非线性影响, 对传输性能的估计十分粗糙, 也没有考虑自相位调制和色散导致的性能劣化影响.因此在前人工作的基础上, 综合考虑线性和非线性影响, 采用光脉冲展宽作为评估指标, 通过理论计算接收端光脉冲的展宽来估计系统传输代价.最后通过仿真验证传输性能评估的可行性和有效性.
2. State Key Laboratory of Information Photonics and Optical Communications, Beijing University of Posts and Telecommunications, Beijing 100876, China
The electric power communication network system as an important information infrastructure of electric system requires high transmission reliability. However, it lacks a clear definition of system reliability and a quantitative measure of the criterion. This article briefly introduced application of transmission performance damage assessment technology in power telecommunication networks, and pointed out the importance of the transmission link damage assessment. The authors used the optical pulse broadening as the evaluation index and calculated the optical pulse broadening to estimate the system transmission penalty. The binary polynomial fitting is used to obtain a more accurate assessment of the linear empirical formula. It was verified by comparing with different simulation parameters to have good feasibility and effectiveness.
光纤作为电力系统通信中主要的传输媒质,为信息传输提供了巨大而廉价的可用带宽,在电力通信网的发展中起着重要作用,通信系统高效运营与电网安全和企业管理的关系日益密切[1-5].
早期的光信号传输质量研究中,没有考虑自相位调制和色散导致的性能劣化影响[6-14].随着电力光网络的容量和规模持续增长,非线性作用对传输性能的影响不能忽视,因此针对电力光传输系统中传输性能不可感知、不可预测、不可控制的问题,保证连接建立和传输性能的可靠性,研究通过输出光信号脉冲展宽和电力光传输系统中非线性损伤的关系至关重要.以往的研究结果表明,在自相位调制受限的系统中输出光脉冲的展宽程度能很好反映系统的非线性损伤[15].
笔者对电力通信网络中非线性传输问题进行建模,并提出利用输出光脉冲展宽评估光信号传输中受到的非线性损伤.首先利用仿真得到光脉冲展宽因素下的系统代价先验值,然后利用线性回归的方法表示系统损伤代价近似公式,最后将各种损伤因素代价叠加起来,得到最终的物理传输性能指标.
1 光脉冲展宽损伤评估理论分析为得到光脉冲展宽与系统性能的关系表达式,笔者进行了一定的理论推导,得到光脉冲展宽的表达式,为第2节的系统仿真与数据拟合做准备.这里将光脉冲的幅度设为A(z, T),它满足非线性薛定谔方程:
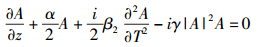
|
(1) |
其中,z为光纤纵向长度,T为传输时间,α为光纤衰减值,β2为色散系数,γ为光纤非线性系数,定义归一化的复幅度U(z, τ)为
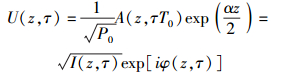
|
(2) |
其中:P0为输入光脉冲的峰值功率,I(z, τ)和φ(z, τ)分别为光强和相位,T0=T/τ,τ为归一化时间.从而式(2) 可以改写为
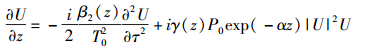
|
(3) |
对于一个由N个光纤跨段组成的系统,光纤损耗由多个光放大器进行补偿.所以有

|
(4) |
其中:ηi为光放大器输出的光功率与输入光功率的比值,Pi为第i光纤跨段的入纤功率.将式(4) 代入式(3) 后可得
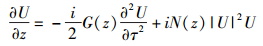
|
(5) |
其中G(z)=β2(z)/T02.令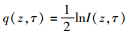
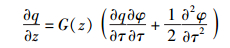
|
(6) |
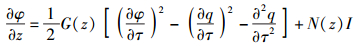
|
(7) |
利用q(z, τ)和I(z, τ)的关系,式(6) 和式(7) 可以分别改写为
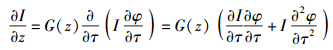
|
(8) |
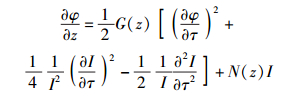
|
(9) |
光脉冲的均方根宽度定义为
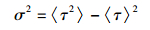
|
其中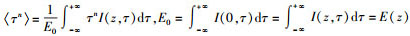
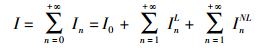
|
(10) |
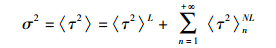
|
(11) |
首先考虑〈τ2〉L,它就是不考虑非线性时脉冲的展宽,可以按照式(12) 进行计算.
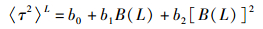
|
(12) |
其中b0, b1, b2为固定系数,B(L)为与L相关的系数,考虑〈τ2〉2NL时忽略掉高阶项的影响,所以有
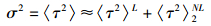
|
(13) |
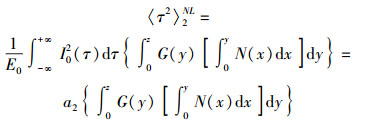
|
(14) |
将式(12) 和式(14) 带入式(13) 中,可以得到脉冲展宽因子的表达式.在本节中以无啁啾高斯脉冲的脉冲展宽因子(σ/σ0)2作为评估对应的物理量.基于数据拟合时的数量级考虑,进行(σ/σ0)2-1变形,采用该参数作为最终的评估量,定义c为光速,λ为光波长,Di为光纤跨段色散值,li为光纤跨段长度,DDCMi为色散补偿光纤值,lDCMi为色散补偿光纤长度,可以得到[15]
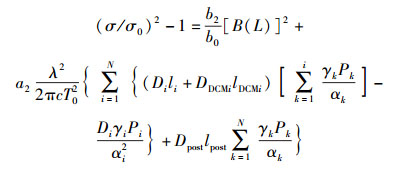
|
(15) |
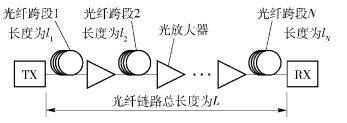
针对上述模型进行了仿真验证,建立了一个电力通信光传输系统.在仿真过程中考虑了一个N跨段光纤传输系统,如图 1所示,光纤链路的总长度为L,第i个光纤跨段的长度li,第i个光纤跨段的非线性系数为γi,第i个光纤跨段入射端处的光功率为Pi,光纤损耗系数为αi,z点处的色散系数为D(z),其中TX, RX分别代表光纤通信系统的发送端和接收端.
|
图 1 电力光纤传输系统示意图 |
电力光纤通信系统中没有采用数字信号处理的方式进行损伤补偿,对色散的补偿需要在链路中串联色散补偿光纤来实现,电力通信网由于部分地区跨度较大,因此系统中放大器需要使用拉曼放大器.因此,在仿真中假设所有的光纤均不考虑偏振模色散,色散补偿光纤不考虑非线性效应,使用拉曼放大器,其增益恰好可以补偿光纤带来的衰减,使得每段光纤入射端的功率相等,且不考虑放大器噪声.
电力通信系统中,光纤跨段长度为100 km,仿真的距离从1 000 km(10个跨段)逐渐增加到1 800 km(18个跨段),每次增加的距离为100 km.仿真功率设置的入射功率为-4~4 dBm,间隔1 dBm,且入射功率为平均功率,可得到81组数据,然后再进行数值拟合,其中参考误码率为10-5.
电力光纤通信系统中由于没有采用数字信号处理的方式补偿色散,因此一般都会采用预色散补偿与后色散补偿.因为实际系统运行过程中的随机性,不可避免将会出现2种情况,即跨段内色散随机变化总色散固定和跨段内色散固定而链路总色散完全补偿.这2种情况都需要进行研究和仿真模拟,以使得在电力通信光网络中使用光脉冲展宽这一损伤评价指标具有更好的适用性和精确性.
2.1 跨段内色散变化,总色散固定时采用完全补偿的色散图,其中每个跨段都由标准单模光纤(SMF, standard single-mode fiber)和色散补偿光纤组成,预色散补偿量Dpre为
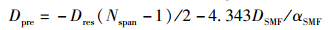
|
(16) |
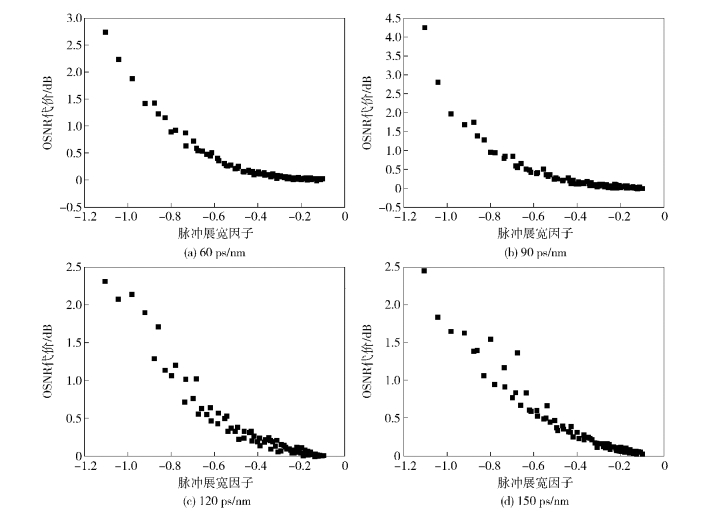
每跨段内残余色散Din变化,接收端后补偿色散量需确保最终的残余色散为0. Dres取值为(60, 90, 120, 150) ps/nm,仿真结果如图 2所示.
|
图 2 每跨段残余色散变化,总残余色散固定时仿真结果对比 |
通过仿真获得光信噪比(OSNR, optical signal to noise ratio)代价值后,首先用3次多项式拟合OSNR代价与脉冲展宽因子之间的关系,然后通过二次拟合得到多项式系数与残余色散之间的关系,最终OSNR代价OPenalty的解析表达式为
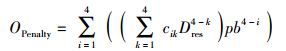
|
(17) |
其中:pb=103[(σ/σ0)2-1],系数矩阵C中各矩阵元素的取值为
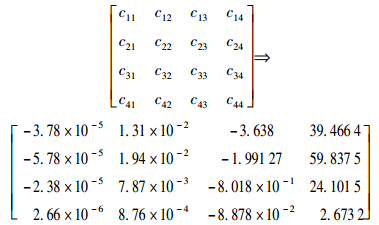
|
可以简单验证拟合表达式(17) 的准确性,取段内残余色散分别为55 ps/nm、145 ps/nm,不同于拟合时所用残余色散值,评估公式计算所得OSNR代价与仿真结果的对比如图 3所示.

|
图 3 仿真结果对比 |
笔者采用了和原有仿真结果不同的参数组合,使得仿真结果和评估公式所得结果具有较好的对应关系,表明评估公式中确定的各参数能满足快速准确的性能评估所需要的要求.
从图 3中可以看出,脉冲展宽因子绝对值较小的区域,评估公式计算所得OSNR代价与仿真结果之间对应得较好,随着脉冲展宽因子绝对值增大,两者之间出现明显差异,但差异不超过1 dB.特别是对于较小的段内残余色散,使用脉冲展宽因子可以获得很好的评估效果.
2.2 跨段内色散固定,总色散变化时预色散补偿如式(16) 所示,每跨段内残余色散固定取值为100 ps/nm,总残余色散取值为(60, 90, 120, 150) ps/nm,后置补偿量根据相应的总残余色散、每段内残余色散、预补偿量来确定,仿真结果如图 4所示.

|
图 4 每跨段残余色散固定,总残余色散变化时仿真结果对比 |
采用的拟合方法与2.1小节相同,同样使用式(17) 作为OSNR代价的解析表达式,其系数矩阵C通过数据拟合得到,各矩阵元素的取值为
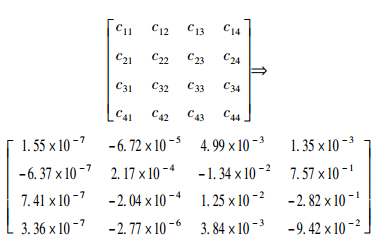
|
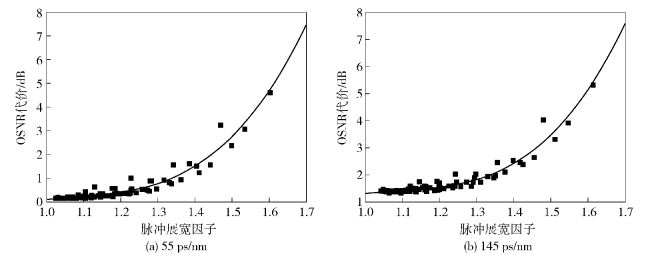
同样为了验证解析表达式(17) 的正确性,将每段残余色散分别取为55 ps/nm、145 ps/nm,通过解析表达式计算OSNR代价并且与仿真结果对比,结果如图 5所示.
|
图 5 仿真结果对比 |
基于脉冲展宽因子的评估公式计算,所得系统代价值与仿真结果之间的对应关系保持得较好,随着总残余色散逐渐增大,两者之间没有出现明显变化,最大差异小于0.7 dB.在累积色散未完全补偿的色散图下,使用脉冲展宽因子作为评估参数较为准确.
3 结束语针对电力通信系统中采用色散补偿光纤补偿色散和拉曼放大器补偿衰减的特点,建立了一个电力通信光纤传输模型,采用脉冲展宽因子作为评估参数,在每段残余色散和最终残余色散分别可变的情况下,进行了大量数值仿真,得到非线性效应和色散联合作用下系统OSNR代价与光脉冲展宽、残余色散之间的对应关系.在采用二元多项式拟合得到较为精确的线性评估经验公式后,选用和拟合时所用数据不同的仿真结果同解析公式计算结果进行比对验证,取得了较好的评估精度.光脉冲展宽因子作为解析化更高的物理量具有更好的应用范围,它不仅在优化的色散图下具有良好的评估能力,而且在非优化的色散图下仍然能达到理想的评估效果.
| [1] |
王明俊. 智能电网热点问题探讨[J]. 电网技术, 2009, 33(18): 9–16.
Wang Mingjun. Some highlights in relation to smart grid[J].Power System Technology, 2009, 33(18): 9–16. |
| [2] |
韩小涛, 尹项根, 张哲. 故障树分析法在变电站通信系统可靠性分析中的应用[J]. 电网技术, 2004, 28(1): 56–59.
Han Xiaotao, Yin Xianggen, Zhang Zhe. Application of fault tree analysis method in reliability analysis of substation communication system[J].Power System Technology, 2004, 28(1): 56–59. |
| [3] |
熊素琴, 周静, 赵子岩, 等. 新一代电力系统自动化通信网络模型与典型网络技术分析[J]. 电网技术, 2010, 34(S2): 434–437.
Xiong Suqin, Zhou Jing, Zhao Ziyan, et al. Analysis on the new model of the communication networks for electric system automation technology[J].Power System Technology, 2010, 34(S2): 434–437. |
| [4] |
张亮, 王建磊, 王福生. 市级电力通信网容灾建设方案研究[J]. 光通信技术, 2009, 33(18): 198–203.
Zhang Liang, Wang Jianlei, Wang Fusheng. Research on disaster recovery construction of the local power communication network[J].Optical Communication Technology, 2009, 33(18): 198–203. |
| [5] |
李春华, 冉静学, 高会生. 基于离差最大化方法的电力通信网传输部分的综合评估[J]. 电力系统保护与控制, 2008, 36(15): 199–203.
Li Chunhua, Ran Jingxue, Gao Huisheng. Comprehensive evaluation of the transmission part of communication network of electric power based on the method of maximizing deviations[J].Power System Protection and Control, 2008, 36(15): 199–203. |
| [6] | Yurong H, Heritage J P, Mukherjee B. Connection provisioning with transmission impairment consideration in optical WDM networks with high-speed channels[J].Journal of Lightwave Technology, 2005, 23: 982–993. doi: 10.1109/JLT.2005.843520 |
| [7] | Ramamurthy B, Datta D, Feng H, et al. Impact of transmission impairments on the teletraffic performance of wavelength-routed optical networks[J].Journal of LightwaveTechnology, 1999, 17(10): 1713–1723. doi: 10.1109/50.793740 |
| [8] | Martins F J F, Bastos F C J A, Arantes E A J, et al. Novel routing algorithm for transparent optical networks based on noise figure and amplifier saturation[C]//Proceedings of IMOC 20032. Iguaza Falls, Brazil: [s.n.], 2003: 919-923. |
| [9] | Pachnicke S, Paschenda T, Krummrich P. Assessment of a constraint based routing algorithm for translucent 10 Gbit/s DWDM networks considering fiber nonlinearities[J].Journal of Optical Networking, 2008, 7(4): 365. doi: 10.1364/JON.7.000365 |
| [10] | Pachnicke S. Fast analytical assessment of the signal quality in transparent optical networks[J].Journal of Lightwave Technology, 2006, 24(2): 815–824. doi: 10.1109/JLT.2005.862472 |
| [11] | Pachnicke S. Physically constrained routing in 10-gb/s DWDM networks including fiber nonlinearities and polarization effects[J].Journal of Lightwave Technology, 2006, 24(9): 3418–3426. doi: 10.1109/JLT.2006.880596 |
| [12] | Pachnicke S, Hecker D N, Spälter S, et al. Experimental verification of fast analytical models for XPM-impaired mixed-fiber transparent optical networks[J].IEEE Photonics Technology Letters, 2004, 16(5): 1400–1402. doi: 10.1109/LPT.2004.826144 |
| [13] | Azodolmolky S, Pointurier Y, Angelou M, et al. A novel impairment aware RWA algorithm with consideration for QoT estimation inaccuracy[J].IEEE/OSA Journal of Optical Communications and Networking (JCON), 2011(3): 290–299. |
| [14] | Xiao Xiaosheng, Gao Shiming, Tian Yu, et al. Analytical optimization of the net residual dispersion in SPM-limited dispersion-managed systems[J].Journal of Lightwave Technology, 2006, 24: 2038. doi: 10.1109/JLT.2006.872278 |
| [15] | Yu Qian, Fan Chongcheng. Analytical study on pulse broadening in chained optical amplifier systems[J].Journal of Lightwave Technology, 1997, 15(3): 444–451. doi: 10.1109/50.557559 |


