2. 西安航空学院 电气学院, 西安 710077
针对无线传感器网络节点能量有限且易失效的问题, 利用复杂网络理论提出了一种能量有效的无线传感器网络无标度拓扑模型.该模型通过节点的剩余能量约束节点的发射半径, 在拓扑演化过程中充分考虑节点剩余能量和节点度等因素, 并引入能量调节参数和节点度调节参数, 得出了一种幂率指数可以在[3, +∞)调节的无标度拓扑结构.动态分析和仿真实验结果表明, 该模型具有无标度网络的幂率特性, 且具有较好的容错性和能耗均衡的特点.
2. College of Electrical Engineering, Xi'an Aeronautical University, Xi'an 710077, China
Considering that the nodes with limited energy are prone to be failure in wireless sensor networks and introducing energy and node degree adjustment parameters, an energy efficient scale-free topology model was constructed based on the complex network theory. The node residual energy is limited according to node radius and topological index can be changed within with full consideration of the factors such as the node residual energy and the node degree. Analysis on the topology dynamic behavior and simulation afterwards show that this model has power rate characteristics of scale-free networks and good fault tolerance and the energy balance characteristics.
无线传感器网络(WSNs,wireless sensor networks)是由基站和大量的传感器节点构成的一种自组织、分布式的网络系统[1],广泛应用于军事、环境监测、交通运输及医疗保健等领域.由于WSNs节点经常布撒在恶劣的环境中,而且通常由能量有限的电池供电,因而节点很容易因能量耗尽和环境破坏引起失效.并且在WSNs拓扑形成以后,很难进行人为干预且网络拓扑容易变化,节点失效后又会引起拓扑分割,直接影响了拓扑的连通度和覆盖率.因此,一种容错性较好的拓扑对于提高WSNs的生命期具有重要的意义,如何节约能量和提高整个网络的容错性成为WSNs研究的重要课题.传统的提高WSNs容错能力的方法多采用的是冗余机制.韩等[2]提出了通过增加中继节点并改变节点通信范围,以实现提高WSNs的容错能力. Misra等[3]研究了如何使用最少的中继节点并保证节点和基站之间的连通,从而提高了WSNs的抗毁性. Bernd等[4]构建了一个能量有效的容错拓扑,即k连通网络(k为网络中的节点个数),使得即使在部分节点失效的情况下,k重覆盖仍然能保持网络的连通性.以上都是通过冗余来提高网络的容错能力,虽然这些方法可以提高网络的容错性,但是却增加了网络的负荷,影响了网络的寿命.近年来,对复杂网络的研究兴起,Barabási和Albert对万维网拓扑结构进行研究时发现其度分布服从幂率分布,他们将具有这种性质的网络称为无标度网络.大量研究表明,容错性不仅存在于冗余网络中,节点度服从幂率分布的无标度网络对节点的随机故障有较强的容错性.为了满足恶劣环境下WSNs容错性的需求,具有无标度特性的WSNs拓扑演化模型引起了国内外学者们的注意.
Zhu等[5]构建了能量有效的WSNs无标度拓扑结构,新加入的节点与网络中已存在的节点相连接的概率取决于节点当前的剩余能量和节点度,促使网络向节能的方向转变.张等[6]在局域世界内构建无标度网络,在连接概率上考虑节点能量、通信流量和连接距离等,在增强网络容错性的同时降低了节点发生相继故障的概率.陈等[7]构建了一种具有无标度特性的局域世界演化模型,提高了拓扑的容错能力,并能节约能量. Zheng等[8]在基于无标度网络的基础上,提出2种WSNs演化模型,在择优连接时考虑节点饱和度和剩余能量等因素,进一步提高了网络的鲁棒性.但是文献[5-8]构建的4种无标度拓扑结构并没有考虑节点通信半径对网络能耗的影响,节点的通信半径越大,节点能耗越快,这样就很容易造成剩余能量小的节点因能量耗尽而失效,从而缩短了网络的生命期.因此,笔者在构建无标度拓扑结构时将会考虑节点通信半径,使通信半径大的节点拥有小的连接概率,从而进一步地均衡网络能耗.并且Zhu等[5-8]构建的拓扑结构幂率指数是一个定值,然而在大多数情况下,WSNs无标度拓扑的幂指数均是可调的,因此幂指数可调的WSNs无标度拓扑结构是目前研究的重点.
根据复杂网络理论,依据WSNs节点的能量与通信半径的关系,提出一种能量有效的无标度拓扑演化模型(EETM,energy efficient topology model),使节点可以根据自身的能量状况选择合适的通信半径,并使剩余能量大的节点拥有较大的连接概率,调节参数的引入,使拓扑的度分布可调,提高了拓扑的应用价值,从而可以满足不同网络性能的需求.
1 EETM演化机制及动态特性分析1.1 EETM拓扑演化模型对网络模型做如下假设.
1) 初始网络由SINK节点以及邻居的m0个节点、e0条边构成,节点在分布区域内均匀分布.传感器节点功率具有可调性,节点可以根据自身的剩余能量情况调节发射功率,确定通信半径.
2) 节点的通信半径可以在R1<R2<…<Rn之间连续切换.当节点的剩余能量小于网络中节点的平均剩余能量时,即Ei<Eave时,节点在R1<R2<…<Rn/2随机选择一个通信半径;当节点的剩余能量大于网路中节点的平均剩余能量时,即Ei>Eave时,节点在Rn/2<…<Rn随机选择一个通信半径.因此每个节点的通信半径会随着节点剩余能量的变化而变化,从而可以有效地调节节点的发射功率,防止节点因能耗过快引起节点失效.
BA(Barabási Albert)模型[8]在择优连接时,新加入的节点与网络中已经存在的节点i相连接的概率仅取决于节点i的度ki,如式(1) 所示,其中i、j表示节点序号.
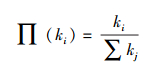
|
(1) |
EETM拓扑演化模型采用经典BA无标度网络的“增长”和“择优连接”原则,拓扑形成分为2个部分.
1) 增长:以少量m0个节点开始,在每一时间步长,向网络中加入一个新节点h,同时加上从此节点出发的m条边;
2) 局域世界择优连接:在择优增长时,新节点h仅在其传输范围内选择连接节点i,且此时的择优连接概率取决于节点当前的通信半径di和节点的度ki,表达式为
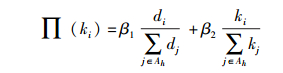
|
(2) |
其中: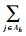
定理 EETM演化模型的度分布是服从[3,+∞)的幂率分布.
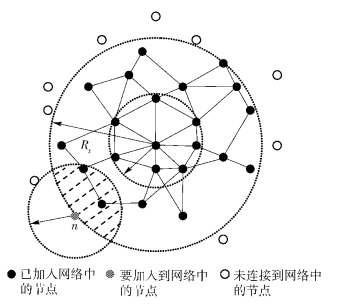
证明 假设新节点n在t时刻加入网络,初始网络的节点数量为m0,初始网络半径为R0,在t时刻的网络半径为Rt,新节点n的通信半径为Rn,如图 1所示.
|
图 1 改进的择优增长过程 |
借助连续场理论,假设节点度ki是连续变化的,则根据1.1节的择优增长过程可知,ki连续变化的速率为
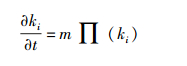
|
(3) |
由于di=f(Ri)为连续函数,由最值定理可得
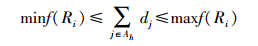
|
(4) |
由中值定理可得,存在ξ使得
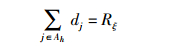
|
(5) |
因监测区域内节点部署服从均匀分布,选择新节点h的邻节点集的概率可由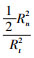
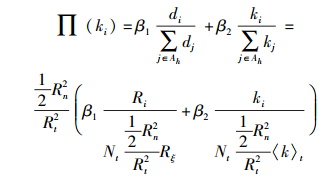
|
(6) |
其中:Nt为t时刻网络节点总数,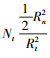
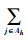
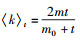
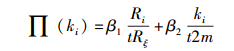
|
(7) |
将式(7) 代入式(3) 可得
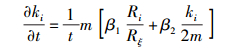
|
(8) |
设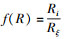
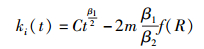
|
(9) |
其中C为任意常数.结合初始条件ki(ti)=m解上述微分方程可得
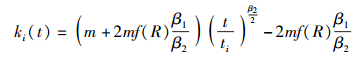
|
(10) |
因此节点i的度小于k的概率为
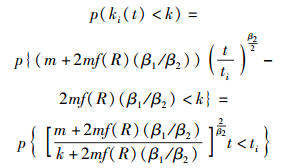
|
(11) |
假设以相同的时间间隔添加新节点到网络中,即各节点加入网络的时间是完全随机的,因此随机变量ti服从(0, t)区间上的均匀分布,其概率密度函数为
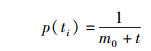
|
(12) |
结合式(11) 和式(12) 可得
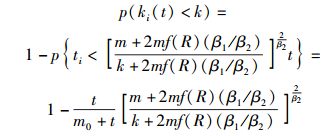
|
(13) |
因此EETM的度分布为

|
(14) |
当t→∞时,式(14) 可化简为
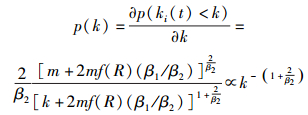
|
(15) |
由式(15) 可知,EETM演化模型的网络拓扑度分布服从幂率分布,幂率指数为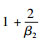
本节对EETM演化模型的度分布和节点度与能量的关系进行Matlab仿真分析,并与BA模型和随机行走模型(ERW,evolution by random walk)进行仿真实验对比,所得仿真结果均为50次实验结果的平均值,并假设传感器节点的通信半径可以在40 m、45 m、50 m之间切换,仿真实验环境参数如表 1所示.
|
|
表 1 环境参数 |
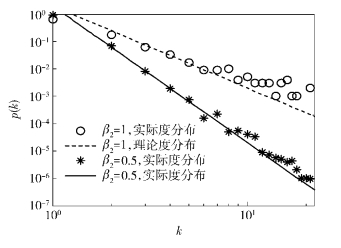
度分布是网络拓扑的重要特征属性,对网络的容错性、可靠性具有重要的影响. 图 2给出了网络规模为200个节点时,β2=1和β2=0.5拓扑的度分布情况.当β2=1时,由理论分析可知,拓扑的度分布符合幂指数为3的幂率分布,并且由图 2可见,拓扑的实际度分布与理论度分布基本一致;当β2=0.5时,拓扑的理论度分布符合幂指数为5的幂率分布,并且由图 2可见,拓扑的实际度分布符合这样的幂率分布.拓扑的度分布随着β2的变化而变化,β2越大,拓扑中度大的节点占有的概率就越大,拓扑就越不均匀,所以可以通过调节β2来调节拓扑的度分布,满足实际网络的需求.
|
图 2 EETM度分布 |
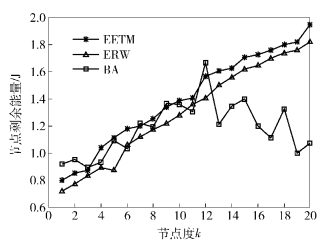
由图 3可以看出,EETM(β2=0.5) 和ERW模型具有节点度越大对应的剩余能量就越大的特点,而BA模型没有这个特点.这是由于BA模型构建拓扑时只与节点度有关,而EETM(β2=0.5) 和ERW模型在构建拓扑时,考虑了节点的剩余能量.由图 3还可以看出,EETM比ERW具有更好的节能优势.这是由于EETM可以根据节点的剩余能量调节节点的通信半径,促使网络向节能的方向转变,从而平衡了网络能耗,避免度大的节点因为能量耗尽引起节点失效,因而延长了网络生命期.
|
图 3 节点度与能量的关系 |
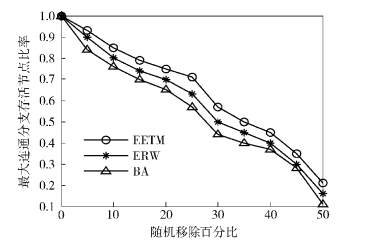
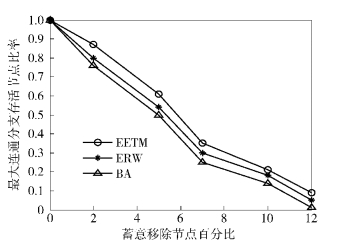
由图 4可知,EETM(β2=0.5) 比ERW和BA模型具有较好的容错性.这是由于EETM(β2=0.5) 在构建拓扑时,不仅考虑了节点的剩余能量,还根据节点的剩余能量调节节点的发射半径,使拓扑向节能、均衡的方向发展,所以比ERW模型具有更好的容错性;而BA模型在构建拓扑时仅考虑了节点度,与节点的剩余能量无关,这样网络中就存在度很大的节点,在应用到WSNs拓扑时,节点由于能量耗尽引起节点失效的概率就比较大,从而影响了拓扑的容错性.由图 5可知,EETM(β2=0.5) 比BA和ERW模型具有更好的容侵性.这是由于EETM构建出的拓扑考虑了节点的发射半径,从而减少了度大的节点的数量,使拓扑的度分布更加均衡,因而增加了拓扑的容侵性.
|
图 4 容错性对比 |
|
图 5 蓄意攻击对比 |
通过构建EETM拓扑模型,综合考虑了节点的剩余能量、通信范围和节点度等因素,并通过节点的剩余能量约束节点的通信半径,使节点避免由于能量耗尽引起节点失效.调节参数的引入,使构建的无标度网络具有幂率指数可调的特点,这样可以满足不同网络性能的需求.采用EETM构造的WSNs具有无标度网络的特征,更加适合WSNs拓扑演化的实际特点,生成的拓扑也具有较好的容错性.
| [1] |
任丰原, 黄海宁, 林闯. 无线传感器网络[J]. 软件学报, 2003, 14(7): 1282–1291.
Ren Fengyuan, Huang Haining, Lin Chuang. Wireless Sensor Networks[J].Journal of Software, 2003, 14(7): 1282–1291. |
| [2] | Han Xiaofeng, Cao Xiang, Errol L, et al. Fault-tolerant relay node placement in heterogeneous wireless sensor networks[C]//Proceedings of the 26th IEEE International Conference on Computer Communications. Washington D C, USA: IEEE, 2007: 1667-1675. |
| [3] | Satyajayant M, Hong Seung Don. Constrained relay node placement in wireless sensor networks to meet connectivity and survivability requirements [C]//Proceedings of IEEE Communications Society Conference on Computer Communications. Phoenix, USA: IEEE, 2008: 879-887. |
| [4] | Bernd T, Heinrich M. Topology control for fault-tolerant communication in highly dynamic wireless net-works[C]//Proceedings of the 3rd International Workshop on Intelligent Solutions in Embedded Systems. Hamburg: IEEE Press, 2005: 89-100. |
| [5] | Zhu Hailin, Luo Hong, Peng Haipeng, et al. Complex networks based energy-efficient evolution model for wireless sensor networks[J].Chaos, Solitons and Fractals, 2009, 41(4): 1828–1835. doi: 10.1016/j.chaos.2008.07.032 |
| [6] |
张德干, 戴文博, 牛庆肖. 基于局域世界的WSN拓扑加权演化模型[J]. 电子学报, 2012, 40(5): 1000–1004.
Zhang Degan, Dai Wenbo, Niu Qingxiao. Local-world weighted topology evolving model for wireless sensor networks[J].Acta Electronica Sinica, 2012, 40(5): 1000–1004. |
| [7] |
陈力军, 刘明, 陈道蓄, 等. 基于随机行走的无线传感器网络簇间拓扑演化[J]. 计算机学报, 2009, 32(1): 69–76.
Chen Lijun, Liu Ming, Chen Daoxu, et al. Topology evolution of wireless sensor networks among cluster heads by random walkers[J].Chinese Journal of Computers, 2009, 32(1): 69–76. |
| [8] | Zheng Gengzhong, Liu Sanyang. Scale-free topology evolution for wireless sensor networks[J].Computers and Electrical Engineering, 2013, 39(6): 1779–1788. doi: 10.1016/j.compeleceng.2013.01.009 |


