2. 武警北京指挥学院, 北京 100012
针对传统安全威胁评估方法难以理解攻击渗透的相关性, 且难以量化相关渗透对于网络环境的影响问题, 结合攻击图渗透动作危害性、渗透相关性和主机业务重要性, 提出双向威胁评估模型和计算方法, 能衡量攻击的深入程度和对目标的威胁程度, 最后提出了一个能应用于实时告警分析的攻击序列评估方法, 并通过实验验证了所提模型的合理性和有效性.
2. Armed Police Beijing Command Academy, Beijing 100012, China
For being not falling in as final targets of attackers, the critical resources in network environments should be protected. It is vital to quantify the threat and impact during the process of multi-stage attacks. Aiming at combine threat quantification of individual attack action and significance value of hosts, as well as large amount of attack dependencies in attack graphs, a methodology for threat evaluation was proposed. The bi-directional threat evaluation presented in this article is able to compute progress attackers already, as well as the threat to goal-resources in attack graph, which can be well applied to real-time attack threat evaluation. The proposed was finally verified in experiment and simulation.
目前,安全威胁的研究工作主要是基于多种安全属性的代数叠加计算和基于攻击类型相关性的综合评估.陈秀真等[1]提出了一个层次化网络安全威胁态势定量评估模型,能直观地给出整个网络系统、主机和服务3个层次的安全威胁态势.刘效武等[2]利用粒子群算法实现D-S(dempster/shafer)证据融合中的权值寻优, 结合对威胁因子和威胁等级函数关系的推演, 提出了面向攻击轨迹的层次化态势评估方法.但以上研究忽略了目标网络中主机和漏洞的相关性和逻辑关系,难以对网络的威胁状态和攻击路径进行预判,而攻击图能在这方面起到很好的补充作用.
目前攻击图的研究集中于整体网络的安全性评估,Pengsu等[3]提出了一种融合了依赖关系的通用漏洞评分系统(CVSS,common vulnerability scoring system)基础分数的聚合方法,能够评估整体网络的安全性. Keramati等[4]使用路径上的CVSS分数的平均值和路径长度的比值来计算攻击发生的可达性.笔者提出的双向威胁评估模型和计算方法,解决了攻击图中的渗透动作相关性带来的评估难题,能应用于实时的态势威胁评估.
1 攻击图定义根据常用的攻击图定义和攻击场景分析,可定义攻击图为

|
1) S为资源状态节点集合
S={si(p, v, h)|i∈(1, N), v∈(0, 10)}为资源状态节点集合.其中,p为状态节点的状态属性信息;v为节点的威胁价值,v=TVL(s), v∈(0, 10);h为状态节点所在的主机. Sinit代表的是初始节点.
2) A为动作节点集合
A={ai(r, l)|i∈(1, M)}.其中,r为该动作节点所表示的漏洞利用信息,包括源和目标主机以及相应的公共漏洞和暴露CVE编号;v为该动作节点的威胁价值,v∈(0, 10);l=VL(ai).
3) O为目标节点集合
O={oi|Oi∈S}, O为一系列需要针对分析的状态节点.
4) E为边集合
E={ei|ei∈((A×S)∪(S×A))},Ef为攻击图资源状态节点和动作节点间的前向指针,Eb=Ef-1为后向指针,表示节点间的逆向关系.其中,状态节点到动作节点的前向指针存在AND、OR和直接推理的逻辑关系;动作节点到状态节点的指针不存在逻辑关系,都是直接推理.
2 基于攻击图双向威胁评估方法2.1 单节点威胁值计算对于攻击图中的动作节点,采用CVSS评价系统中的当前度量标准temporal metrics作为评分参考,该评分能定量地描述攻击者利用该漏洞后造成的影响程度和难易程度.
动作节点a的威胁值:
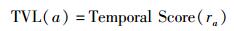
|
对于攻击图中的状态节点,都会有1个与主机威胁相关的价值衡量Score,和CVSS的Temporal Score一样,可以设置为0~10区间的分数.
状态节点s的威胁值:

|
其中:hsrc为源主机,hdst为目标主机.
2.2 双向威胁距离计算双向威胁距离包括初始威胁距离,即与初始节点的逻辑距离;目标威胁距离,即与目标节点之间的逻辑距离.这两个逻辑距离就能定量地判断该节点的攻击深入程度和对目标的潜在威胁程度,进而判断网络态势.
2.2.1 逻辑距离的计算在初始威胁距离的计算中,给定目标攻击GA=(S, A, O, E).在初始威胁距离的计算中,Qand(v)表示节点v的前序节点所经过的前件关系为AND的节点所组成的队列,times(k, Qand(v))表示节点k在Qand(v)出现的次数,dtimes(k, Qand(v))表示节点k在Qand(v)被处理过的次数,RDin(Qand(v))和RDgl(Qand(v))分别表示初始威胁距离和目标威胁距离中需要处理的重复加权路径.
重复加权距离RD(Qand(v))的计算如下:
1) 遍历Qand(v),找出所有times(k, Qand(v))-dtimes(k, Qand(v))>1的节点k;
2) 对于第1) 步中的节点k,dtimes(k, Qand(v))=times(k, Qand(v))-dtimes(k, Qand(v))-1;
3) 最后,计算重复加权路径RD(Qand(v), W)=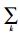
初始威胁距离:
1) 当与前件关系为AND时,有
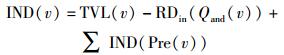
|
2) 当与前件关系为OR时,有
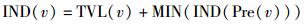
|
3) 初始威胁距离中的重复路径为
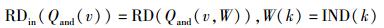
|
目标威胁距离:若∃times(k, Qand(v))>1, GLD(v)=-RDgl(Qand(v))+ ∑GLD(Post(v));否则,GLD(v)=TVL(Post(v))+MIN(GLD(Post(v))).目标威胁距离中的重复路径RDgl(Qand(v))=RD(Qand(v, W)), W(k)=GLD(k)+TVL(k).
在目标威胁距离的计算中,衡量的是每个节点到目标节点的逻辑距离,Qand(v)表示节点v的后序节点所经过的前件关系为AND的节点.若times(k, Qand(v))-dtimes(k, Qand(v))>1,说明后件序列含有未处理的重复路径. RDgl(Qand(v))表示目标威胁距离中需要处理的重复加权路径.
2.2.2 算法复杂度分析若攻击图中的状态节点数量为s,动作节点的数量为a, 有向边的数量为e,AND节点的最大Qand队列的长度为c,所有节点的最大前件数量是P.由于Qand的长度是随着搜索的深入依次增长的,所以根据平均情况,逻辑距离计算的时间复杂度为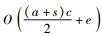
在基于攻击图的告警关联中,攻击告警首先会根据告警的漏洞属性和目标IP网络地址映射到相应的攻击图节点上[5-6],形成告警序列后就可以做威胁评估.
检测完成度(PM,process metric)表示作为告警输入的IDS对目标网络的检测的完整情况.威胁度(TM,threat metric)表示现有攻击序列对于目标节点的威胁情况. xeq代表攻击序列.
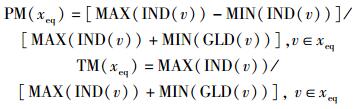
|
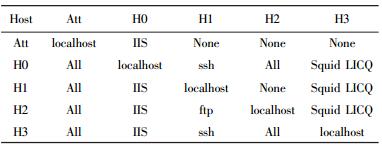
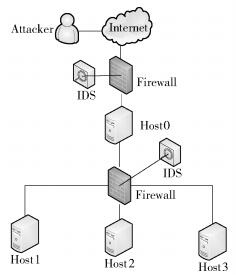
以图 1中的真实网络和3个规模不同、复杂性也不同的网络为例,验证所提方法的合理性和有效性.实验环境是Intel i5-2430M@2.40 GHz处理器、2 GB内存、Windows 7,算法在Microsoft Visual Studio用C#实现. Host0是运行在Windows NT4.0上的IIS Web Server,Host1的系统平台是Windows 2000 sp2,上面运行了FTP和SSH服务;Host2的系统是Windows XP,上面运行了Netbios-ssn服务;Host3是Redhat Linux 7.0系统,上面运行的服务有LICQ、Squid、Mysql Database. Host3是作为攻击者的目标主机,其上的Mysql数据库中的数据是重要资源,也是攻击者的目标.
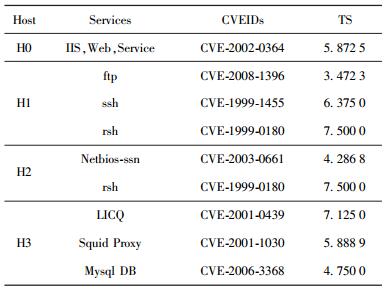
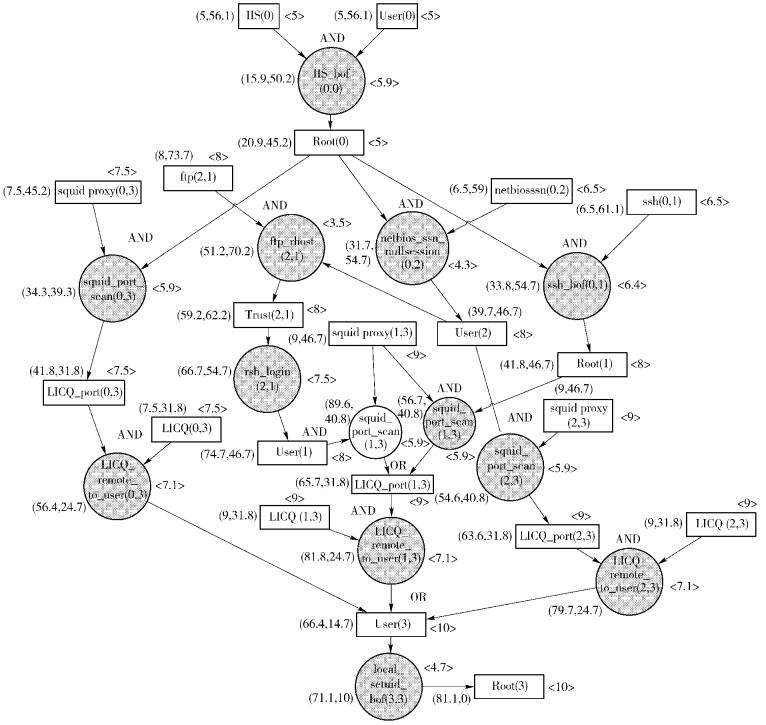
使用Nessus对图 1中的4台主机进行漏洞扫描,能得到各主机上的脆弱性信息,根据其CVE编号查询美国国家数据库即可得出表 1中主机漏洞的得分情况.结合表 2和表 3中的防火墙规则、主机连通性情况和主机漏洞情况,可以构建出图 2所示的攻击图;同时,根据相应的漏洞评分和主机评分表,可以得出每个动作节点和状态节点的威胁值,最后利用2.2节中的双向威胁计算方法即可得出每个节点的初始威胁距离和目标威胁距离,均标记在图 2中节点旁的括号中.从表 4中可以看出,随着攻击路径的增长,威胁度持续上升.
|
图 1 实验环境 |
|
|
表 1 主机评分表 |
|
|
表 2 防火墙规则表 |
|
|
表 3 主机漏洞分布表 |
|
图 2 实验攻击图 |
|
|
表 4 攻击路径和威胁度计算 |
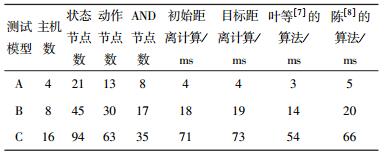
为了测试提出的算法,建立了3个不同复杂度和规模的网络模型,测试的结果如表 5所示.从测试结果可以看出,随着目标网络中的主机的增长,产生的攻击图中的节点数目和有向边的数目也在急剧上升,同时从算法的运行时间可以看出,提出的算法由于需要重复比对AND关系的节点队列,在算法性能上略差于叶等[7]的算法和陈[8]的算法.
|
|
表 5 不同规模和复杂度的网络的算法运算结果对比 |
讨论了攻击图中的威胁评估问题,结合漏洞和状态之间的因果关系和逻辑关系,提出双向威胁距离计算的方法,能利用攻击图中的因果关联和与或条件关系,计算出初始威胁距离和目标威胁距离,并提出了能应用于实时网络检测中的攻击序列的威胁评估方法.最后在真实环境的实验中表明了方法的合理性和有效性.
| [1] |
陈秀真, 郑庆华, 管晓宏, 等. 层次化网络安全威胁态势量化评估方法[J]. 软件学报, 2006, 17(4): 885–897.
Chen Xiuzhen, Zheng Qinghua, Guan Xiaohong, et al. Quantitative hierarchical threat evaluation model for network security[J].Journal of Software, 2006, 17(4): 885–897. |
| [2] |
刘效武, 王慧强, 禹继国, 等. 基于多源融合的网络安全态势感知模型[J]. 解放军理工大学学报:自然科学版, 2012, 13(4): 403–407.
Liu Xiaowu, Wang Huiqiang, Yu Jiguo, et al. Network security situation awareness model based on multi-source fusion[J].Journal of PLA University of Science and Technology(Natural Science Edition), 2012, 13(4): 403–407. |
| [3] | Cheng Pengsu, Wang Lingyu, Jajodia S, et al. Aggregating CVSS base scores for semantics-rich network security metrics[C]//Reliable Distributed Systems (SRDS), 2012 IEEE 31st Symposium on. Irvine, CA: IEEE, 2012: 31-40. |
| [4] | Keramati M, Akbari A, Keramati M. CVSS-based security metrics for quantitative analysis of attack graphs[C]//Computer and Knowledge Engineering (ICCKE), 2013 3th International Conference on. Mashhad: IEEE, 2013: 178-183. |
| [5] | Ahmadinejad S H, Jalili S, Abadi M. A hybrid model for correlating alerts of known and unknown attack scenarios and updating attack graphs[J].Computer Networks, 2011, 55(9): 2221–2240. doi: 10.1016/j.comnet.2011.03.005 |
| [6] | Wang Lingyu, Liu Anyi, Jajodia S. Using attack graphs for correlating, hypothesizing, and predicting intrusion alerts[J].Computer Communications, 2006, 29(15): 2917–2933. doi: 10.1016/j.comcom.2006.04.001 |
| [7] |
叶云, 徐锡山, 贾焰, 等. 基于攻击图的网络安全概率计算方法[J]. 计算机学报, 2010, 33(10): 1987–1996.
Ye Yun, Xu Xishan, Jia Yan, et al. An Attack Graph-Based Probabilistic Computing Approach of Network Security[J].Chinese Journal of Computers, 2010, 33(10): 1987–1996. |
| [8] | 陈锋. 基于多目标攻击图的层次化网络安全风险评估方法研究[D]. 长沙: 国防科学技术大学, 2009. |