为了提高正交频分复用(OFDM)系统定时同步的抗窄带干扰能力, 利用加扰的思想对Park算法的前导符号进行了改进, 并提出了新的定时测度函数.通过TU-6多径信道下的仿真表明, 在窄带干扰的影响下改进算法仍能保持尖锐的相关峰值特性, 实现准确的定时估计, 同时其性能会随着子载波数的增加得到提升.此外, 改进算法也降低了相关旁峰的大小, 提高了定时同步的抗噪声能力.
In orthogonal frequency division multiplexing (OFDM) systems, the validity and accuracy of symbol timing synchronization is seriously impacted by narrowband interference that cannot be eliminated by conventional algorithms. To improve the performance, a new timing metric was proposed with help of a scrambling operation to the preamble symbol in Park's algorithm. Simulations are carried out in TU-6 multipath channel under the narrowband interference. It is shown that the improved algorithm successfully obtains the needed sharp correlation peak to realize accurate timing synchronization. Furthermore, with increase of the number of sub-carriers, the anti-narrowband-interference performance can be obviously promoted. In addition, the improved algorithm also reduces the size of the correlation sub-peaks, which improves the anti-noise performance.
OFDM调制技术以其抗多径、抗频率选择性、高频谱利用率的优势,被广泛应用于无线局域网、数字电视、电力线通信等宽带通信系统[1-2].然而,OFDM传输系统对定时同步误差非常敏感,为了提高同步的可靠性,多在数据帧的头部插入专门设计的前导符号用于同步[2-4],典型的如Schmidl、Minn和Park算法,以Park算法的性能尤为突出[4].但是Park算法与Minn算法同样具有较大的旁峰特性,影响了低信噪比下的同步性能,对此诸多文献提出了相应的加权同步算法[4].
然而,在一些实际应用的OFDM系统中,由于频谱共享或载波泄漏,可能会引入窄带干扰(NBI, narrowband interference)信号[5-6],严重影响了定时同步的可靠性.为了改善定时同步的抗NBI性能,文献[5-7]在同步之前采用自适应滤波或频域检测,以减小NBI的影响,但同时也增加了同步的复杂度.为了提高NBI环境下的定时同步效率,Liu[2]提出了一种基于循环扩展前导符号的自相关算法,不需要进行额外的滤波和频域检测,但由于其相关峰的平滑特性,严重降低了多径信道下的同步性能.
笔者基于Park算法,提出了一种改进的抗NBI定时同步算法,改进了前导符号结构,保留了尖锐的相关峰值特性,并对符号前半序列进行加扰,抑制了旁峰,同时提高了定时同步的抗NBI性能.
1 OFDM信号模型在OFDM基带模型中,发送的OFDM符号时域序列可以描述为
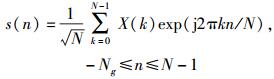
|
(1) |
其中:X(k)为调制到第k个子载波上的数据,Ng为循环前缀的长度,N为子载波数目.当N足够大时,s(n)可以被认为是均值为0、方差为E(|s(n)|2)=σs2的复高斯随机变量[6].
在系统接收端,考虑NBI的影响,接收信号r(t)经过T0=1/B(B为OFDM符号带宽)周期采样后,可以表示为[2, 4]

|
(2) |
其中:δ为定时采样偏移;ζ为归一化频率偏移,以载波间隔Δf=B/N为单位;{h(l)}为信道冲击响应序列,L为序列的长度;bm=b′mejϕm,而b′m、ϕm和ζm分别为第m个NBI信号的幅度、相位和归一化频率,M为NBI信号的数目;w(n)为均值为0、方差为σn2的复高斯白噪声采样值.因此,系统的信噪比和信干比可以分别表示为γn=σs2/σn2和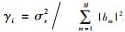
Park算法采用了和Schmidl算法相同的前导符号结构[3],可以同时完成定时和频率偏移的估计,同时由于符号采用二相相移键控调制,时域上后N-1序列成中心共轭对称,因此其定时测度定义为[3]
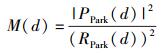
|
(3) |
其中:

|
(4) |
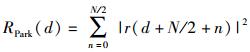
|
(5) |
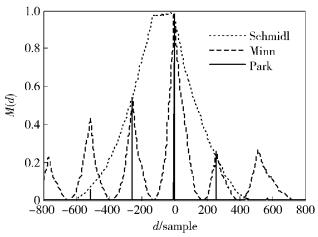
图 1所示为N=1 024、Ng=64、δ=0、ζ=0.25、γn=20 dB时,Schmidl、Minn及Park算法在加性高斯白噪声(AWGN, additive white Gaussian noise)信道下的M(d)曲线,由图 1可以看出,与Schmidl和Minn算法相比,Park算法具有更加尖锐的峰值特性,其在正确的符号起始点d=0处具有一个明显的脉冲峰值,且峰值周围的M(d)几乎为0,可以实现更加准确的定时同步;但同时也可以发现Park算法和Minn算法一样,在符号非正确起始点处存在多个较大的旁峰值,当d=-N/4时,其旁峰值最大,接近主峰的40%,在低信噪比下易引起定时位置的误判.
|
图 1 在AWGN信道下Schmidl、Minn、Park算法的定时测度比较 |
Park算法虽然提高了定时同步的准确度,但是和Schmidl、Minn等传统算法一样,没有考虑NBI的影响,以下是对Park算法的NBI影响分析.
将式(2) 代入式(4),根据{h(l)}、{s(n)}、{w(n)}、{ej2πζmn/N}的独立非相关性[2],当N足够大时,其滑动自相关值可化简为
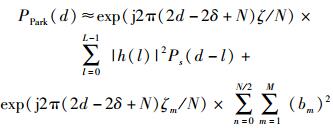
|
(6) |
其中Ps(d) = 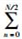
为了简化对NBI影响的分析过程,选取AWGN信道,假设M=1和b1为实数,则式(6) 可表示为
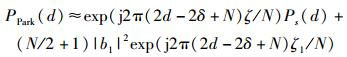
|
(7) |
由式(7) 可以看出,PPark(d)不仅与发送序列的对称相关值Ps(d)和频偏ζ有关,还与NBI的频率ζ1和幅度|b1|密切相关,从而增加了PPark(d)的不确定性,严重降低了定时同步的可靠性.
将式(2) 代入式(5),同理RPark(d)可以化简为
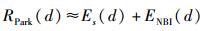
|
(8) |
其中: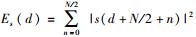
因此,当ζ-ζ1∈{±i/2,i∈奇数}时,其定时测度在正确起始点处,即M(δ)取最小值:
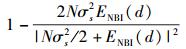
|
(9) |
而在非正确起始点处,有
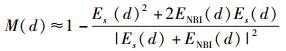
|
(10) |
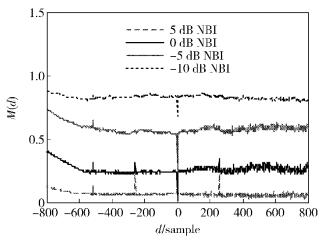
所以当γi≥0 dB时,所有的M(d)≥M(δ),即正确起始点处的定时测度为最小值. 图 2所示为N=1 024、Ng=64、δ=0、ζ=0.25、γn=20 dB时,Park算法在AWGN信道下受不同信干比NBI影响的定时测度曲线,其中ζ-ζ1=-587.5,属于{±i/2,i∈奇数}.如图 2所示,当γi=0 dB、-5 dB、-10 dB时,其定时测度在正确起始点处为最小峰值,而非最大峰值,将会给定时偏移估计带来严重的误差.
|
图 2 Park算法在AWGN信道下受不同信干比NBI影响时的定时测度曲线(ζ1=587.75) |
为了抑制NBI对定时同步的影响,对Park算法的前导符号结构做以下的改进:
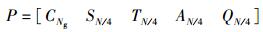
|
其中:AN/4为N/4长度的随机序列;QN/4为AN/4的共轭对称序列,SN/4和TN/4为利用加扰因子(-1)n分别对AN/4和QN/4进行加扰而产生的序列,CNg为Ng长度的循环前缀序列.
此时,当正确接收到前导符号时,利用(-1)n与前半部分序列相乘去除加扰因子后,前后半序列共轭对称相关.因此,将定时测度定义为
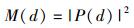
|
(11) |
其中
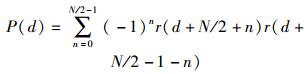
|
(12) |
根据式(12),正确起始点处M(d)取最大值,所以定时偏移可以估计为
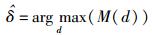
|
(13) |
同时,由于去除加扰因子后,符号具有和Schmidl算法同样的重复结构,可以同时完成健壮的频率偏移估计.
3.2 改进算法的性能分析改进算法继承了Park算法的对称相关特性,当OFDM系统中存在NBI时,其相关函数P(d)具有和式(6) 相同的形式,其后一项可进行以下化简:
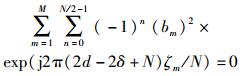
|
(14) |
因此其定时测度可以不受NBI的影响,从而提高了算法的抗NBI能力.此外,当d=δ-N/4或d=δ+N/4时,由于(-1)n的存在,对称相关的序列通过式(12) 求和后,正负相互抵消,避免了定时测度如Park算法出现较大的相关旁峰,因而也提高了定时同步的抗噪声能力.
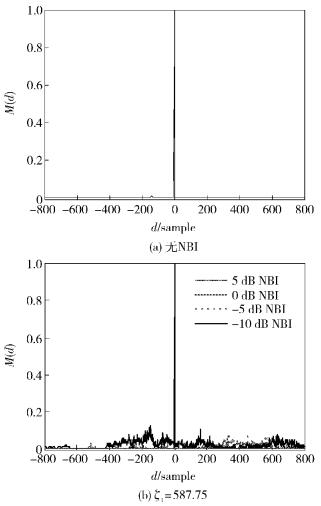
图 3(a)和(b)分别为,N=1 024、Ng=64、δ=0、ζ=0.25、γn=20 dB时,改进算法在无NBI和ζ1=587.75的NBI AWGN信道下的定时测度曲线.由图 3(a)可以看出,改进算法的定时测度在正确起始点处,和Park算法一样存在一个明显的脉冲峰值,便于对定时位置的估计;同时改进算法具有极小的旁峰,在低信噪比下可以提供准确的定时估计.由图 3(b)可以看出,改进算法的定时测度在NBI的影响下仍然可以保持尖锐的峰值特性,随着NBI的增大,旁峰值会有所增加,当γi=-10 dB时其旁峰值仍小于主峰值的20%,对定时估计的准确度有较小的影响.
|
图 3 改进算法在AWGN信道下的定时测度曲线 |
在仿真实验中,OFDM系统的主要参数为带宽B=7.61 MHz、子载波数目N=1 024、保护间隔Ng=64[8]及频率偏移ζ=0.25,信道采用典型的城市环境多径信道模型TU-6[8],连续仿真1万次.而NBI的频率ζm和ϕm则是分别在[0, N-1]和[-π, π]内随机产生的.为了验证改进算法的适用性,还通过改变参数N对改进算法进行了相应的仿真.
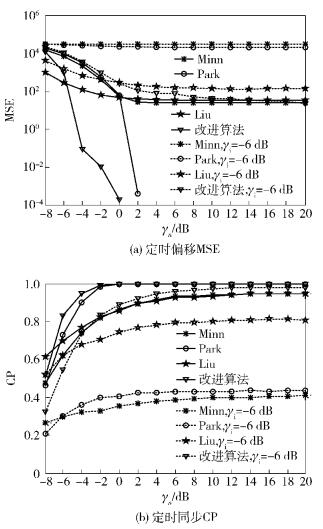
为了验证改进算法的性能,本文分别对改进算法与Minn、Park、Liu算法的定时偏移均方差(MSE, mean square error)和定时同步正确率(CP, correct probability)进行了仿真.定时同步CP取定时误差位于[-Ng+L, 0]范围内的概率[7]. 图 4(a)和(b)分别给出了Minn、Park、Liu以及改进算法,在不同信噪比多径信道下,无NBI和受γi=-6 dB NBI影响时的定时偏移MSE和同步CP.由图 4可以看出,无NBI影响时,改进算法比Minn算法、Park算法有更小的MSE和更高的CP,尤其是在-4~1 dB的信噪比条件下,具有低于10-1的MSE和大于0.94的CP,在低信噪比下也能完成精确的定时同步;而与Liu算法相比,当γn>-6 dB时,改进算法的MSE明显小于Liu算法,CP也远高于Liu算法,具有更好的定时同步性能.当γi=-6 dB时,Minn和Park算法的MSE一直保持在104~105之间,CP小于0.5,无法完成有效的定时同步;而改进算法在γn>4 dB时,CP达到了0.94以上,明显优于Liu算法.
|
图 4 不同信噪比多径信道下的定时偏移MSE和同步CP |
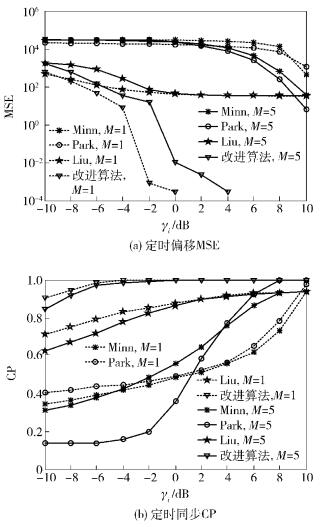
图 5(a)和(b)分别为当γn=20 dB时在不同信干比多径信道下的定时偏移MSE和同步CP仿真曲线.由图 5可以看出,随着γi的减小,Minn和Park算法的MSE明显增大,CP也急剧下降,无法完成有效的定时同步;而改进算法和抗NBI的Liu算法一样,明显抑制了MSE的增长和CP的下降趋势,但与Liu算法相比,改进算法具有更小的MSE,其CP也有了明显的提高,在M=1和γi=-10 dB时,CP高达0.903 0,提高了将近20%,可实现更加准确的定时估计.如图 5所示,当NBI的个数M从1增加到5时,在低信干比的环境下,改进算法的定时同步性能损失了将近2 dB,优于Liu算法的4 dB.
|
图 5 不同信干比多径信道下的定时偏移MSE和同步CP |
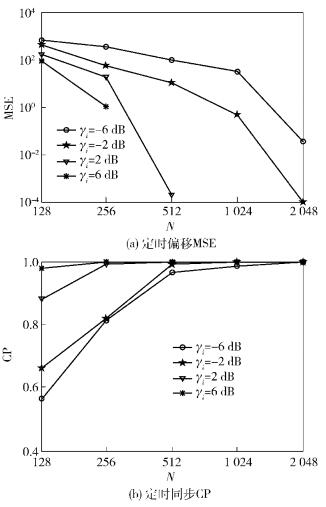
此外,为了进一步验证改进算法的适用性,针对不同N的系统环境,在γn=20 dB和M=1的多径信道下,对改进算法进行了仿真. 图 6(a)和(b)分别为γi=-6 dB、-2 dB、2 dB、6 dB时的定时偏移MSE和同步CP曲线,可以看出随着N的增大,MSE逐渐减小,CP也会逐渐提高.当N≥512时,在γi=-6 dB的NBI影响下,改进算法的CP仍能大于0.95,具有较好的抗NBI特性;当N=256或128时,在γi≥2 dB的NBI影响下,其CP保持在0.9左右,也能实现准确的定时同步.
|
图 6 不同N的系统环境下的定时偏移MSE和同步CP |
为了提高OFDM符号定时同步的抗NBI特性,基于Park算法提出了改进算法,对前导符号的前半序列进行了加扰.仿真结果表明,改进算法在NBI的影响下仍具有尖锐的峰值特性,与抗NBI的Liu算法相比,改进算法具有更小的定时偏移MSE和更高的定时同步CP.同时,由于加扰因子的引入,改进算法具有较小的旁峰特性,可用于低信噪比下的定时同步.此外,当NBI较小时,改进算法在N=256或128的OFDM系统中也能完成准确的定时同步.
| [1] | Jing Qingfeng, Cheng Ming, Lu Yuping, et al. Pseudo-noise preamble based joint frame and frequency synchronization algorithm in OFDM communication systems[J].Journal of Systems Engineering and Electronics, 2014, 25(1): 1–9. doi: 10.1109/JSEE.2014.00001 |
| [2] | Liu Sisong, Yang Fang, Song Jian, et al. OFDM preamble design for synchronization under narrowband interference[C]//Power Line Communications and Its Applications (ISPLC), 2013 17th IEEE International Symposium on. Johannesburg: IEEE Press, 2013: 252-257. |
| [3] | Park B, Cheon H, Kang C, et al. A novel timing estimation method for OFDM systems[J].IEEE Communications Letters, 2003, 7(5): 239–241. doi: 10.1109/LCOMM.2003.812181 |
| [4] | Xie Zhiyuan, Luo Lei, Dong Fenfen, et al. An improved synchronization algorithm for OFDM based powerline communication[C]//Power Engineering, Energy and Electrical Drives (POWERENG), 2013 4th IEEE International Conference on. Istanbul: IEEE Press, 2013: 1613-1618. |
| [5] | Coulson A J. Narrowband interference in pilot symbol assisted OFDM systems[J].Wireless Communications, IEEE Transactions on, 2004, 3(6): 2277–2287. doi: 10.1109/TWC.2004.837471 |
| [6] |
郝士琦, 赵福才, 胡以华. 窄带干扰情况下定时序列检测性能分析[J]. 北京邮电大学学报, 2009, 32(4): 104–108.
Hao Shiqi, Zhao Fucai, Hu Yihua. Analysis of the narrowband interference effect on timing sequence detection performance[J].Journal of Beijing University of Posts and Telecommunications, 2009, 32(4): 104–108. |
| [7] | Moretti M, Cosovic I. OFDM synchronization in an uncoordinated spectrum sharing scenario[C]//IEEE Global Telecommunications Conference (GLOBECOM). Washington D. C. : IEEE Press, 2007: 3796-3801. |
| [8] | ETSI. TS 102 863 V1. 2. 1-2012, Implementation guidelines for a second generation digital terrestrial television broadcasting system (DVB-T2)[S]. France: ETIS, 2012: 22-24. |


