2. 内河航运技术湖北省重点实验室, 武汉 430063;
3. 武汉理工大学 信息工程学院, 武汉 430070
事件区域检测是无线传感器网络在复杂环境感知中的一项重要应用, 然而节点受到环境中多种不确定性因素(如温度、湿度、硬件条件等)的影响导致其感知数据出现错误, 降低了节点对事件检测的准确度.根据邻近节点之间的感知信息存在一定的空间相关性, 提出一种基于网络拓扑的节点感知信任度模型, 在此基础上每个节点将自身感知信息与邻居节点交换信息相结合, 建立贝叶斯事件检测容错模型, 计算事件发生的预测概率, 同时确定事件发生的最优阈值, 节点根据概率预测结果与最优阈值相比较对事件发生做最终决策.仿真结果表明, 与典型的贝叶斯最优阈值容错算法相比, 在节点故障率为25%的情况下, 所提算法可将错误节点修正率由65%提高到78%;而在节点故障率为30%的情况下, 所提算法可将错误节点修正率由50%提高到70%, 体现出了良好的容错性能.
2. Hubei Inland Shipping Technology Key Laboratory, Wuhan 430063, China;
3. School of Information Engineering, Wuhan University of Technology, Wuhan 430074, China
Event area detection is one of the most important applications in complex environment for wireless sensor networks. The nodes in the networks may have faults due to many uncertainty factors (such as temperature, humidity, hardware etc.), which will reduce event detection quality. Considering the spatial correlation for the sensing information of neighboring sensors, a belief model based on network topology was proposed. A Bayesian fault tolerance model was further constructed by synthesizing sensor's own information and its neighbor nodes' information. The model can predict the probability as well as the optimum threshold on whether the event happens. The node makes the final decisions by comparing the two probability values. Simulations show that compared with the optimal threshold decision scheme, the proposed scheme can increase the percentage of the corrected nodes from 65% to 78% when node fault probability is 25%. The scheme can also increase the percentage of the corrected nodes from 50% to 70% when the node fault probability is 30% that reflects better fault-tolerance performance.
无线传感网络被广泛应用在环境监测、目标追踪、工业过程控制、网络质量监测等方面,受到节点数量大、处理能力有限等因素的制约,无线传感网络通常是以自组织的方式对感知到的信息进行分布式处理,来实现对于监测环境的异常事件检测[1].在实际应用中,由于传感器节点的不可靠性,使得信息在感知和通信过程中出现故障,造成误检或者漏检,进而严重影响事件检测的性能.
针对这一问题,通过定义节点的检测状态,考虑节点信息之间的空间相关性,利用邻居节点的信息和贝叶斯方法,开展了最早的传感网络的事件容错检测的研究[2-4].但在实际应用中,无线传感网络由于其应用环境、传感器节点的不同硬件条件、节点的调度次数不同等原因,使得节点的感知错误率不相同.在考虑传感网络在检测过程中的异构性基础上,提出了无线传感网的异构事件容错检测方法[5].同时,传感器节点的信息还具有时间相关性,利用这一特性学者们开展了利用节点的时间-空间相关信息的特性来实现事件容错检测的相关研究[6-8].在空间相关性研究中,由于节点间不同的距离对于节点信息之间的影响是不同的,学者们通过将节点间距离的进行归一化处理,将节点间距离的影响进行量化,进一步的优化了事件容错检测的算法[9].但由于节点拓扑位置关系的影响,使得不同节点信息感知的相似度和可靠度存在差别.
笔者在考虑节点的空间相关性的基础上,针对这一问题,通过分析节点的拓扑位置关系和信息感知可信度关系,提出一种节点的感知信任度模型来表示节点信息的贡献度的方法,再利用不同贡献度的信息来提高事件检测的准确性和可靠性.
1 事件检测问题描述事件是一组事件属性的组合,通过时间信息、空间信息和属性信息描述了发生在一定监测区域内的一个感兴趣的状态.在事件检测无线传感器网络中,事件区域内部及其附近的节点感知信息存在空间关联性,距离越近的节点,感知信息的相关性就越强.针对该问题,首先对无线传感器网络检测环境做以下基本假设:监控区域中布设n个同构的传感器节点,且所有节点的地理位置已知,节点集合表示为I={i}, 1≤i≤n;在网络中,节点读数以二进制形式表示,Ti(t)=0表示无事件区域节点,Ti(t)=1表示事件区域节点;对于在t时刻的任意节点i来说,用Si(t)表示观测值,定义Si(t)=1表示观测有事件发生,Si(t)=0表示观测没有事件发生,Ri(t)表示估计读数;节点发生故障的概率均为p,则网络中故障节点期望值为np,非故障节点期望值为n(1-p).考虑在比较复杂的环境中会出现节点无效、测量数据受干扰、节点设备故障及节点误判等情况,其中最主要的情况表现为在无事件发生时节点读数为1,以及在有事件发生时节点读数为0[2-3].按照这个定义,可以认为节点故障概率为
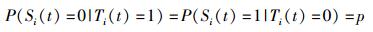
|
(1) |
在传感器网络事件检测中,事件的空间关联是指节点i的感知信息与邻居节点具有一定的相关性,且距离越近相关性越强,其观测数据越接近节点i的观测数据.因此,网络节点的位置分布对事件检测准确与否有很大关系,可以利用节点间的距离参数来反映节点i与其邻居节点j∈F(i)间采样数据的相似程度,参数值越大,说明邻居节点的采样数据在节点i的事件检测判断中起的作用越大,反之则越小.
基于以上思路,考虑事件发生区域邻近节点感知数据的相似性,获得节点i的邻居节点集合为F(i)={Sj(t), dij≤r},即节点i与其邻居节点j∈N(i)间的距离dij≤r(r为节点感知半径).记邻居节点的个数为N(i),对于节点i来说,定义邻居节点j∈F(i)的感知信息对其决策的贡献度权重值wij为

|
(2) |
由式(2) 可知,所有邻居节点的加权和为1.节点i的置信度为
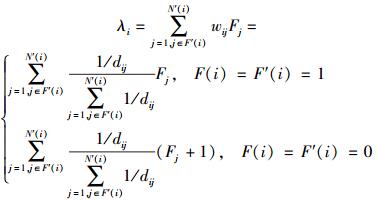
|
(3) |
其中:F′(i)为与节点i的读数相同的邻居节点集合,N′(i)为F′(i)的个数.
2.2 节点感知信任度模型在节点协同条件下的事件检测过程中,节点的可信度不仅来自自身的感知信息,也来源于对邻居节点感知信息的判断.从某种意义上来说,节点信任度是指一个节点对其他节点是否能正确地提供感知对象信息的主观判断,其依据来源于所有邻居节点对是否有事件发生的判断结果,引入信任评估可以有效地消除不良节点的影响. Ui表示中心节点(节点自身)与邻居节点之间的感知信任度,是通过节点间的信息交换来获得的,主要作用是根据邻居节点的判断来增加中心节点的信任能力,提高节点检测的可信度.节点感知信任度定义为邻居节点与中心节点的信息近似程度,因此可以采用强化学习方法得到中心节点的感知信任度Ui,更新公式表示为
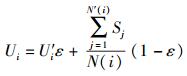
|
(4) |
其中:U′i为节点自身的感知信任度;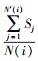
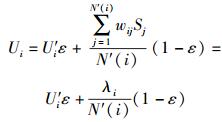
|
(5) |
节点对相邻节点的信任度以一个0~1之间的实数Ui来表示,Ui=0表示完全不信任,Ui=1表示完全信任.假设设置Ui的初始值为0.5,ε=0.5.当一个节点Si=1,其邻居中有4个读数为Sj=1的节点,且这4个节点到中心节点i的贡献度权重值为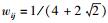
根据文献[2]中的节点决策主观概率计算公式,并利用2.2节提出的可信度模型对主观概率模型加以改进,邻居节点中有k个节点的读数为a,节点i的读数为a,得到节点i根据邻居节点的感知信息判断为a的条件概率为
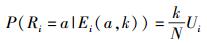
|
(6) |
节点的决策是由自身感知信息和邻居节点感知信息融合得到的,利用贝叶斯条件概率,可以得到邻居节点的先验概率为E,节点i的观测值为b时,节点i的估计值为a(需要考虑a与-a (非a)2种情况)的条件概率为

|
(7) |
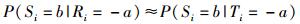
|
在基于网络拓扑的节点感知可信度的容错机制分析基础上,利用贝叶斯方法得到节点i对邻居节点j∈F(i)的主观置信度的概率估计为
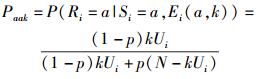
|
(8) |
由于节点发生故障属于独立事件,且故障率为p,则可以得到N个邻居节点中有k个没有出错的概率为
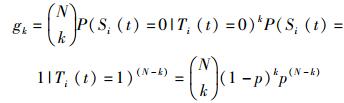
|
(9) |
由式(9) 得到

|
(10) |
对J(a, i)求关于k的连续导数,可以得到
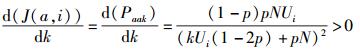
|
(11) |
则得到k的最小值为
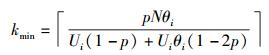
|
(12) |
其中θi为判断阈值
通过容错分析后网络中平均错误个数为
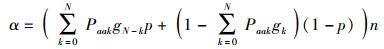
|
(13) |
为了使α值最小,当p<0.5时,通过文献[3]的分析,当kmin=kmin*=0.5(N-1) 时,可以得到最优阈值,并代入式(12),得到
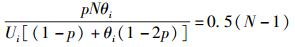
|
可以得到阈值θi为
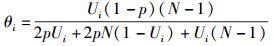
|
(14) |
由式(14) 可知,当Ui=1时,得到文献[2]中的最优阈值θ*为
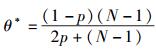
|
(15) |
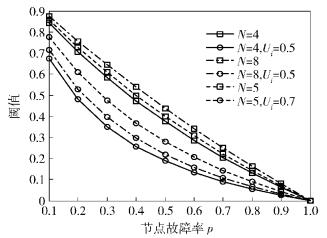
为了比较式(14) 与式(15) 中的参数对阈值的影响,得到如图 1所示的分析.由图 1可以看出,阈值随着节点故障率的增大而减小,当邻居节点个数相同时,考虑节点可信度的阈值较低,提高了节点的容错能力;当节点可信度相同时,邻居节点个数的多少对节点的容错能力影响较小.
|
图 1 节点故障率与阈值间的关系 |
在实际的事件检测节点容错中,考虑事件的属性检测数据具有不确定性及网络节点分布差异性,对事件节点的影响可能会随节点对所检测事件的重要程度、节点间的距离等发生变化.在这种条件下,为了提高节点对事件状态决策的可靠性,将提出的容错算法用于校正节点误报、漏报等情况,并进行修正以提高事件检测的正确性.在节点感知信息可信度基础上进一步建立事件容错机制,按照3.1节推导的容错决策模型,对任意节点i来说,若Paaki>θ,则Ri(t)=Si(t),反之Ri(t)=-Si(t).
基于节点感知信任度模型的分布式容错(FED-BM, fault-tolerance event detection based on belief model)算法步骤如下.
1) 根据式(2) 确定各邻居节点的距离权重wij,具体步骤如下.
① 计算传感器节点i与其周围节点间的距离dij;
② 如果满足判断条件dij≤r,则将节点j存入F(i);
③ 利用式(2) 计算F(i)内的距离权重wij;
2) 计算节点概率Paaki,并根据与阈值的比较做出最终判断,具体步骤如下.
① 利用节点i自身及其邻居节点的信息计算节点i的可信度Ui;
② 基于贝叶斯条件概率,进行二进制判决,得到二进制估计值Paaki;
③ 若Paaki>θ,则Ri(t)=Si(t),反之Ri(t)=-Si(t).
4 理论分析与仿真实验4.1 理论分析在仿真过程中,用以下参数作为分布式容错算法性能评估指标.
1) 检测错误率ε(修正后的总错误数):检测错误的节点数目与事件区域总节点数目的比值.
2) 误判率δ(新增的错误节点数):事件未发生时,检测到事件的节点数目与事件区域总节点数目的比值.
3) 失判率γ(没有修正的错误节点数):事件发生时,未检测到事件的节点数目与事件区域总节点数目的比值.
4) 容错率β(原本为错误后修正正确的节点数):最终状态为故障的节点数目与事件区域内总故障节点数目的比值.
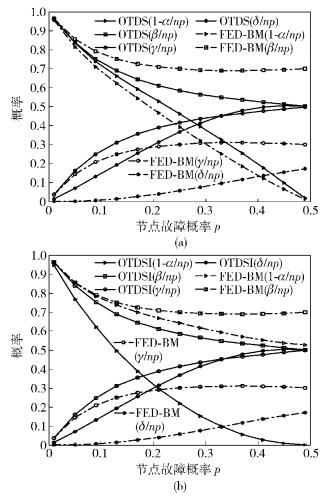
图 2所示为利用提出的FED-BM方法与文献[2]和文献[3]中的贝叶斯随机阈值决策检测方法(OTDS,optimal threshold decision scheme)比较的结果. 图 2(a)与(b)中均采用随机阈值决策,取节点的平均可信度Tr为0.6,邻居节点数N为4.相比于文献[2]中的OTDS算法与文献[3]中的OTDSI算法可以看出,FED-BM算法在提高检测概率与降低错误概率方面表现出了明显的优势.如图 2(a)所示,当节点故障率p=0.2时,OTDS算法容错率为60%左右,但FED-BM算法提高到71%左右;同时,引入错误的概率利用FED-BM算法比利用OTDS算法从30%降低到2%左右.另一方面,如图 2(b)所示,当节点故障率p=0.2时,OTDSI算法事件检测概率为30%左右,而FED-BM算法可以提高到70%左右.
|
图 2 不同算法性能理论分析 |
本节利用Matlab仿真软件,对无线传感器网络环境下的事件检测性能进行评价.假设在30×30的区域内均匀的布设900个节点,p=0.1,每个节点的通信半径为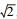
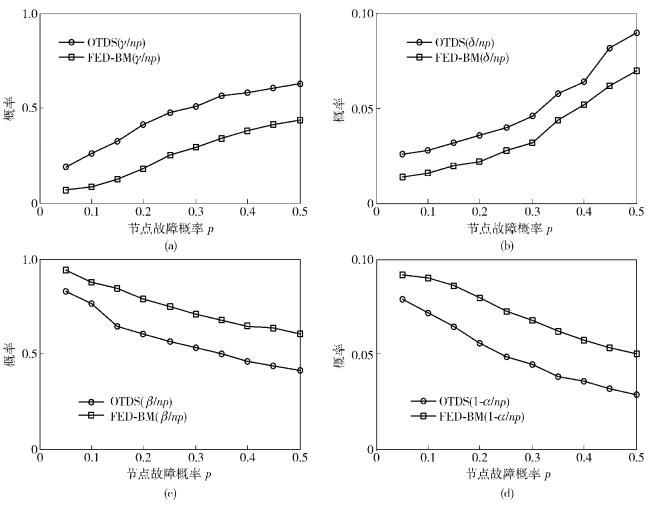
由图 3可知,随着节点故障率p的增加,FED-BM算法的各性能均好于OTDS算法. 图 3(a)给出了网络中平均未改正错误的概率,当节点故障率p为30%时,利用OTDS算法仍然存在50%的错误节点未改正,而利用FED-BM算法将降低到30%左右. 图 3(b)给出了网络中平均引入错误的概率,随着节点故障率p的增加,2种算法均会引入错误,但FED-BM算法比OTDS算法引入的错误少.由图 3(c)给出的平均改正错误的概率分析结果可以看出,当节点故障率p为25%时,利用OTDS算法改正错误概率接近65%左右,而利用FED-BM算法将提高到78%左右. 图 3(d)给出了修正后平均错误概率,可以看出FED-BM算法比OTDS算法低.
|
图 3 事件检测性能仿真结果 |
从上述分析中可知,引入节点可信度可以提高事件检测质量,降低引入错误概率,但由于邻居节点数对容错检测的影响,需要综合考虑节点可信度和邻居节点数目两方面因素.
从上述分析中可知,引入节点可信度可以提高事件检测质量,降低引入错误概率,但由于邻居节点数对容错检测的影响,需要综合考虑节点可信度和邻居节点数目两方面因素.
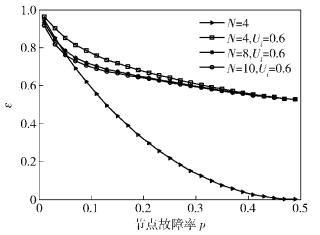
由图 4所示的分析结果可以看出,传感器网络节点邻居与节点可信度对事件检测具有一定的影响.其中,受节点邻居数目影响较小,如当节点故障率p=0.3,节点邻居数目分别为4、8、10时,检测错误概率之间相差不到2%;但受到节点可信度的影响较为明显,当节点故障率p=0.3,节点邻居数目为4时,检测错误概率为15%左右,而考虑节点可信度时,检测错误概率达到67%左右.
|
图 4 节点故障率与事件检测概率之间的关系 |
笔者充分考虑了无线传感网络中节点信息的空间相关性,通过分析节点的拓扑位置关系和信息感知可信度之间的关系,提出了一种基于节点感知信任度模型的无线传感网络事件检测方法.通过实验分析证明,该算法较之前的经典算法具有较好性能.但研究过程中,没有考虑位于事件区域边缘节点的容错问题.因此,未来的工作中,将考虑边缘节点的事件检测问题,建立事件边界容错检测模型.
| [1] | Akyildiz I F, Su W, Sankarasubramaniam Y, et al. A survey on sensor networks[J].IEEE Communication Magazine, 2002(8): 103–114. |
| [2] | Krishnamachari B, Iyengar S. Distributed bayesian algorithms for fault-tolerant event region detection in wireless sensor networks[J].IEEE Transactions on Computers, 2004, 53(3): 241–250. doi: 10.1109/TC.2004.1261832 |
| [3] | Chen Qingchun, Lam Kam-Yiu, Fan Pingzhi. Comments on distributed bayesian algorithms for fault-tolerant event region detection in wireless sensor networks[J].IEEE Transaction on Computers, 2005, 54(9): 1182–1183. doi: 10.1109/TC.2005.140 |
| [4] | Luo Xuanwen, Dong Ming, Huang Yinlun. On distributed fault-tolerant detection in wireless sensor networks[J].IEEE Transactions on Computers, 2006, 55(1): 58–70. doi: 10.1109/TC.2006.13 |
| [5] | Ould-Ahmed-Vall E, Ferri H B, Riley G F. Distributed fault-tolerance for event detection using heterogeneous wireless sensor networks[J].IEEE Transactions on Mobile Computing, 2012, 11(12): 1994–2007. doi: 10.1109/TMC.2011.194 |
| [6] | Moradi M, Ghaisari J, Askari J, et al. A new method for detection of a distributed event in wireless sensor networks[C]//ICEE 2011. Tehran: IEEE, 2011: 1-5. |
| [7] |
董传明, 刘克中, 罗广, 等. 无线传感器网络环境下的一种轻量级事件容错检测算法[J]. 传感技术学报, 2014, 27(1): 135–141.
Dong Chuanming, Liu Kezhong, Luo Guang, et al. A light weight fault-tolerant event detection method in wireless sensor networks[J].Chinese Journal of Sensors and Actuators, 2014, 27(1): 135–141. |
| [8] | Wu Tao, Cheng Qi. Online dynamic event region detection using distributed sensor networks[J].Aerospace and Electronic Systems, IEEE Transactions on, 2014, 50(1): 393–405. doi: 10.1109/TAES.2013.120308 |
| [9] | Li Ping, Li Hong, Wu Min. Distributed event region fault-tolerance based on weighted distance for wireless sensor networks[J].Journal of Systems Engineering and Electronics, 2009, 20(6): 1351–1360. |


