对于实时性要求较高的人脸识别算法, 图像特征表示不仅应该具有高的区分能力, 还应该具有较小的空间维数.提出了一种基于主导近邻像素的局部Gabor空间直方图(LGSH-DNP)的图像特征表示方法.首先, 对人脸图像进行Gabor滤波, 滤波后图像上的每个像素用其邻近的两个最大的像素的位置表示并编码成该像素的描述符; 然后, 提取描述符所形成图像的空间直方图; 最后, 采用加权交集直方图相似度来度量空间直方图之间的距离, 从而实现人脸图像识别.在人脸识别技术图像库上的实验结果表明, 该图像特征算法具有较高的识别率和较低的计算复杂度.
For face recognition system used in real-time application, the image feature representation should not only have high discriminative capability, but also the low dimensionality. A new face image representation-local Gabor spatial histogram based on the dominant neighboring pixel (LGSH-DNP) was proposed. Firstly, the face image is filtered by the Gabor filter bank. Each pixel of the resulted filtered images is labeled by the positions of the two neighboring pixels with the highest values, resulting in multiple descriptor images. Secondly, the spatial histogram is extracted from these descriptor images. Finally the weighted intersection histogram similarity measure is used to realize face classification. Extensive experiments are performed on face recognition technology face image database. It verifies the effectiveness of the proposed LGSH-DNP method.
当前,人脸识别技术(FERET,face recognition technology)已广泛应用于生活中的各个方面,如基于图像特征的信息检索、基于图像识别的购物推荐、人脸支付、虚拟社交、三维建模等.人脸识别算法一般来说包括特征提取和分类器构造两大步骤.其中,提取高效的图像特征对最终识别性能的提高具有至关重要的作用[1-2].所提取的图像特征不仅应具有较强的区分力,而且还应具有较小的空间维数以降低计算复杂度.
Gabor滤波器和局部二值模式(LBP,local binary pattern)算子是两种互补且非常有效的人脸识别方法[3],局部Gabor二值模式直方图序列[4](LGBPHS,local Gabor binary pattern histogram sequence)采用Gabor LBP的直方图序列来表示人脸图像,Gabor相位模式直方图[5](HGPP,histogram of Gabor phase patterns)结合了Gabor滤波器输出的幅度部分和相位部分,取得了很高的识别精度.但这些算法的特征描述符空间维数很大,因而算法的运行需要较高的计算和存储资源.为了解决这一问题,提出了一种基于主导近邻像素的局部Gabor空间直方图(LGSH-DNP,local Gabor spatial histogram based on dominant neighboring pixel)的人脸图像特征.基于该特征的人脸识别算法的识别率与LGBPHS、HGPP相近,而特征描述符的维数却远远地小于它们.
1 LGSH-DNP人脸图像特征的提取1.1 Gabor滤波Gabor滤波器实质上是尺度(均方差)为1/fν的二维高斯低通滤波器被方向为φμ,频率为fν的复平面正弦波调制后的输出.选取不同的方向φμ和尺度1/fν可得到包含不同方向和尺度的多个Gabor滤波器的滤波器组.
Gabor滤波响应图像Fμ, ν(x, y)可以表示为人脸图像f(x, y)与Gabor滤波函数ψμ, ν(x, y)的卷积:
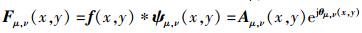
|
(1) |
其中:*表示卷积运算,Aμ, ν(x, y)和θμ, ν(x, y)分别为Gabor滤波响应的幅度和相位.局部Gabor主导近邻像素(LG-DNP,local Gabor-dominant neighboring pixel)特征是从Gabor幅度响应图像(GMI)上提取的.
1.2 LG-DNP特征图 1给出了LG-DNP特征的编码方案.如图 1(a)所示,GMI图像上的每一像素由其8-邻接像素包围着,每个邻接像素的位置用一个3位二进制代码表示.首先对这8邻接像素的像素值进行排序,然后选取最大的2个邻接像素并对其位置进行编码.若有多个邻接像素同时具有最大值,则取具有较小位置代码的邻接像素进行编码.如图 1(b)所示,编码值为min(8D1+D2, 8D2+D1),其中D1和D2分别为最大和第二大的2个像素的位置代码. LG-DNP编码方案共有Npattern=C82=28种码型.

|
图 1 LG-DNP编码方案 |
通过从每幅GMI图像中提取LG-DNP特征,得到了人脸图像的如图 2所示的5行8列共40幅LG-DNP图像. 图 2(a)中的5行8列图像分别表示从5种尺度和8种方向的Gabor滤波响应幅度图像(GMI)上提取的LG-DNP特征. 图 2(b)给出了图 2(a)中最左上角图像经过8×8分割后的效果.

|
图 2 采用LG-DNP编码方案得到的LG-DNP图像及分割 |
LG-DNP得到人脸图像在多个方向和尺度上的分量图像,并且捕获了分量图像每个像素的2个主导方向,包含了丰富的图像纹理信息.图像纹理的方向对亮度的变化不敏感,因此LG-DNP对亮度变化具有较强的鲁棒性.同时,由于LG-DNP抛弃了含有较多噪声的非主导方向的信息,因此对噪声不敏感.
1.3 LGSH-DNP空间直方图的计算LG-DNP特征采用空间直方图作为人脸图像的特征描述符.首先将每个LG-DNP图像分割成M=Vpattern×Hpattern个互不重叠的矩形区域,其中Vpattern和Hpattern分别表示在垂直方向和水平方向上分割的区域的数目.如图 2(b)所示,每幅LG-DNP图像被分割成了8×8个互不重叠的矩形区域;然后计算每个区域内表征各码型出现频数的直方图;最后将所有的直方图序列连接起来便形成了空间直方图.空间直方图刻画了图像中不同位置的各个码型出现的频数.
方向为μ,尺度为ν的LG-DNP图像的第p个区域Rμ, ν, p的直方图Hμ, ν, p中码型为l的直条的频数可表示为
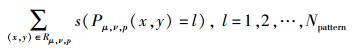
|
(2) |
其中:Pμ, ν, p(x, y)为位于区域Rμ, ν, p的坐标为(x, y)的像素的LG-DNP码型,l为一有效码型,Npattern为1.2节中所描述的编码方案码型数量. s(·)∈{0, 1}为一布尔条件指示函数,则
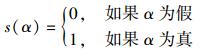
|
(3) |
人脸图像的空间直方图LGSH-DNP为LG-DNP图像的各个区域的直方图向量依次连接,可表示为
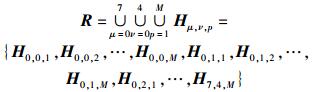
|
(4) |
其中:R为人脸图像的空间直方图LGSH-DNP,M=Vpattern×Hpattern为每个LG-DNP图像所分割的区域的数量;操作符∪表示将5×8×M个直方图向量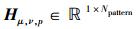
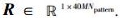
LGSH-DNP特征之间的相似度采用直方图交集来度量.两个直方图序列H1和H2的交集相似度度量可表示为
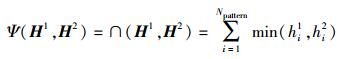
|
(5) |
其中:Npattern为直方图的直条数量,即1.2节所描述的LG-DNP编码码型的数量;hi1和hi2分别为直方图序列H1和H2的第i个直条的频数;∩表示求交集的操作符.由于直方图H1和H2的各直条频数值之和相等,即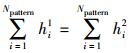
空间直方图序列是由多个直方图序列连接而成的,因此两幅人脸图像的空间直方图R1和R2的交集直方图相似度为各个对应直方图相似度之和,即
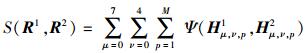
|
(6) |
设wμ, ν, p为直方图序列Hμ, ν, p的权值,则加权交集直方图相似度S′(R1, R2)为
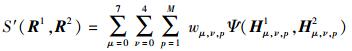
|
(7) |
为了评估LGSH-DNP人脸识别算法的性能,在大型人脸图像FERET[1]数据库上测试其Rank-1识别率(人脸识别算法输出一个身份结果的识别率),并与最新发表的识别算法的测试结果进行比较.为了比较的方便,采用FERET数据库提供的标准的测试协议.该测试协议给出了1个图像模板集(gallery)和4个测试集(probe set). 4个测试集FB、Fc、Dup.Ⅰ和Dup.Ⅱ分别用来测试人脸识别算法在表情变化、亮度变化、短的时间间隔和长的时间间隔下的性能.
3.1 不同的图像区域加权值的计算及分析在计算LGSH-DNP之间的加权交集直方图相似度时,需要首先获得各个区域的权值wμ, ν, p.每个区域权值应该与训练集中任意两幅图像在该区域的直方图是否表示同一人的区分力成正相关.区分力越强,分配的权值越大,反之越小[4-5].在计算出训练集中每个人在方向为μ,尺度为ν的LG-DNP图像的第p个区域的直方图之后,将该区域的不同图像的直方图之间的相似度分为两类:同一人的相似度(within persons similarities) Ωw和不同人的相似度(between persons similarities)Ωb.用Fisher分类准则(FSC,Fisher separation criterion)函数[4-5]来评估直方图对类Ωw与类Ωb之间的区分力:
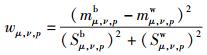
|
(8) |
其中:wμ, ν, p为在方向为μ,尺度为ν的第p个区域所分配的权值;mμ, ν, pw和mμ, ν, pb分别为类Ωw与类Ωb的均值;(Sμ, ν, pw)2和(Sμ, ν, pb)2分别为类Ωw与类Ωb的样本方差.式(8) 右边分子部分为类间离差度,分母部分为类内离差度.
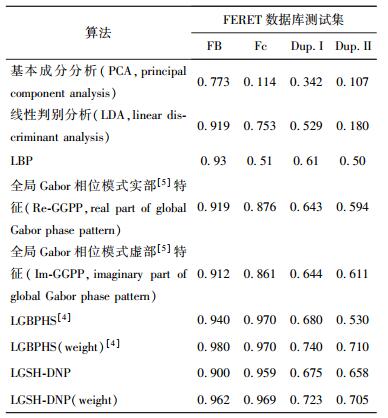
3.2 与其他人脸识别算法性能的比较分析为了评估LGSH-DNP算法的性能,对LGSH-DNP算法和目前所知的已发表的识别算法在FERET人脸数据库上的Rank-1识别率进行了比较. 表 1给出了比较结果,其中LGSH-DNP (weight)表示加权后的LGSH-DNP算法.
|
|
表 1 LGSH-DNP算法与其他识别算法在FERET数据库上的Rank-1识别率 |
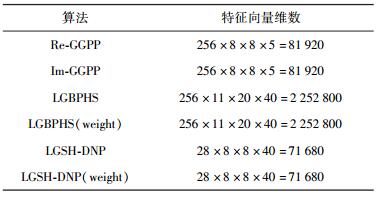
表 2给出了LGSH-DNP算法和一些最新人脸识别算法特征向量的维数.对于GGPP和LGBPHS等这些利用Gabor滤波和空间直方图作为特征向量的算法,其特征向量的长度L可表示为

|
(9) |
|
|
表 2 一些人脸识别算法的特征向量的维数 |
其中:Npattern为各个区域的直方图的直条的数量,Vpartition和Hpartition分别为每个LG-DNP图像在垂直方向和水平方向上分割的区域的数量,NGabor为Gabor滤波器组中包含的滤波器的数量.
由表 1可以看出,LGSH-DNP(weight)算法的Rank-1识别率远远高于PCA、LDA、LBP.同时结合表 2可以看出,LGSH-DNP(weight)的Rank-1识别率高于具有相似特征向量维数的Re-GGPP和Im-GGPP算法.
虽然LGSH-DNP(weight)的性能略低于LGBPHS(weight)的性能,但由表 2可知,前者的特征向量的维数仅仅是后者的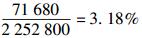
提出了基于LGSH-DNP特征的人脸识别算法,该算法具有较高的识别性能和较低的计算复杂度. LGSH-DNP特征采用了Gabor滤波器优良的尺度和方向选择性的特点,同时用占主导作用的近邻像素对每个滤波后的图像像素进行编码.实验表明LGSH-DNP的性能超过了具有相似特征向量维数其他算法的性能.虽然与目前最新的识别算法LGBPHS相比,LGSH-DNP算法的识别率略低,但其计算复杂度却远远地小于它.高的性能-复杂度比的特性使得LGSH-DNP算法非常适合于那些对计算和存储资源要求苛刻和对实时性要求较高的应用场合.
| [1] | Phillips P J, Moon H, Rizvi S A, et al. The feret evaluation methodology for face-recognition algorithms[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(10): 1090–1104. doi: 10.1109/34.879790 |
| [2] |
聂祥飞, 郭军, 杨震. 基于小波变换的人脸检测[J]. 北京邮电大学学报, 2006, 29(3): 114–117.
Nie Xiangfei, Guo Jun, Yang Zhen. Face detection based on wavelet transform[J].Journal of Beijing University of Posts and Telecommunications, 2006, 29(3): 114–117. |
| [3] | Tan Xiaoyang, Triggs B. Enhanced local texture feature sets for face recognition under difficult lighting conditions[J].Image Processing, IEEE Transactions on, 2010, 19(6): 1635–1650. doi: 10.1109/TIP.2010.2042645 |
| [4] | Zhang Wenchao, Shan Shiguang, Gao Wen, et al. Local gabor binary pattern histogram sequence (lgbphs): A novel non-statistical model for face representation and recognition [C]//Tenth IEEE International Conference on Computer Vision (ICCV). Beijing: IEEE Press, 2005: 786-791. |
| [5] | Zhang Baochang, Shan Shiguang, Chen Xilin. Histogram of gabor phase patterns (hgpp): A novel object representation approach for face recognition[J].Image Processing, IEEE Transactions on, 2007, 16(1): 57–68. doi: 10.1109/TIP.2006.884956 |