2. 清华大学 计算机系, 北京 100084
针对骨干边缘分离网络下自私性对边缘自治域入流量规划的影响, 提出了基于联盟博弈的入流量规划模型.该模型以网络开销作为入流量规划性能的评价指标, 建立了网络开销与网络运营商收益的关系.边缘自治域通过与其他自治域形成联盟, 优化其入流量规划性能, 提高其网络运营商的收益.同时, 分析了联盟核心的特点, 并提出基于SHAPLEY值的收益分配方法.仿真结果表明, 基于联盟博弈的入流量规划方法能提高边缘自治域的入流量规划性能, 基于SHAPLEY值的收益分配方法实现了加入联盟核心的边缘自治域收益的公平分配.边缘自治域能否组成联盟受到运营商收益与入流量规划性能关系的影响.
2. Department of Computer Science and Technology, Tsinghua University, Beijing 100084, China
The impact of selfishness on edge autonomous systems under transit-edge separated Internet was analyzed, and an incoming traffic engineering model based on coalition games was proposed. This model uses network cost as evaluation metrics for incoming traffic engineering performance and establishes relationship as well between network cost and revenues of Internet service provider when this edge autonomous systems(AS) is operating. The coalition achieves maximum revenues by decreasing network cost of the edge AS. Furthermore, the characteristic of coalition was illustrated, followed by the revenue allocation method based on SHAPLEY value. Simulation shows that the incoming traffic engineering based on coalition games can decrease network cost of edge ASes, and the revenue allocation method based on SHAPLEY value is fair to edge ASes joining the core of the coalition. Besides, it is shown that the relationship between revenues and network cost affects the result whether edge ASes can form a coalition.
入流量规划对边缘自治域具有重要意义.然而,边缘自治域的入流量规划不由其自己控制,而最终由其他自治域决定.随着网络架构的发展,一种重要的趋势是骨干边缘分离网络(LISP, locator identifier separation protocol)[1],这种网络架构为边缘自治域合作进行入流量规划提供了接口[2-3].
笔者以特定边缘自治域为研究对象,在入流量规划性能影响网络运营商(ISP, Internet service provider)收益的假设下,研究边缘自治域如何通过合作最大化收益,进一步分析如何分配由合作带来的收益增益.首先分析LISP下边缘自治域的数据传递过程及边缘自治域自私性特点;然后提出基于联盟博弈的入流量规划模型,并提出联盟博弈的核心求解方法及基于SHAPLEY值的收益分配方法;最后通过仿真实验验证联盟博弈的性能.
1 LISP架构及自私性特点在骨干边缘分离网络中,骨干自治域和边缘自治域在不同的地址空间.骨干自治域所在的地址空间为路由地址(RLOC, routing locator), 边缘自治域所在的地址空间为用户识别(EID, endpoint identifier). EID在边缘自治域标识用户,RLOC在骨干自治域标识边缘自治域的边缘路由.边缘路由的功能是为边缘自治域和骨干自治域交换数据提供接口.
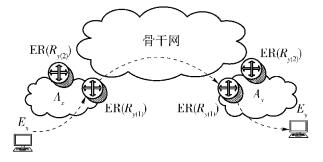
如图 1所示,以边缘自治域Ax的用户Ex向边缘自治域Ay的用户Ey发送数据包的过程分析LISP的数据传输过程.首先,Ex根据域内的路由协议(如最短路径)将数据包发送到Ax中的某个边缘路由(如Rx(1)). Rx(1)通过EID-RLOC查询机制(查找能到达EID的RLOC)发现Ey可以通过Ay中的边缘路由Ry(1)或边缘路由Ry(2)到达.
|
图 1 LISP架构下的数据包传递过程 |
根据LISP的路由规则[1], Ay可以在EID-RLOC查询数据库设置其边缘路由(Ry(1)和Ry(2))的权重,以期影响其他自治域(如Ax)的路由选择决定.例如,为了入流量平衡,Ay可能希望Rx(1)将数据包由Ry(2)发送给Ey.然而,如何发送数据包最终由Ax决定.比如,由于时延、路由表复杂度等原因,Ax可能希望将Rx(1)发出的数据包通过Ry(1)发送到Ey.在这种情况下,Ax和Ay的路由选择出现了冲突,即Ax没有按照Ay的需求选择路径发送数据包.这种冲突的出现本质上是由于边缘自治域的自私性引起的,即仅希望最大化自己的利益,而不管是否会损害到其他自治域的性能(如入流量是否平衡).当很多自治域都采用这种方式进行路由时,那么可能导致某个边缘自治域的入流量不平衡,降低该边缘自治域ISP为用户提供的服务质量,最终影响该ISP的收益.
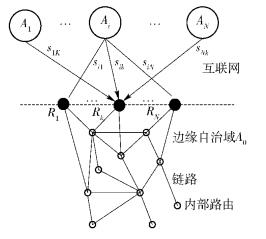
2 联盟博弈入流量规划2.1 模型建立下面以任意一个边缘自治域A0为例分析其入流量规划的模型.如图 2所示,边缘自治域A0有K个边缘路由器R1, …, Rk, …, RK. N个边缘自治域A1, …, Ai, …AN有发送到A0的流量需求s1, s2, …, sN. Ai(i≠0) 向A0的Rk发送的流量为sik,sik的大小由Ai(i≠0) 决定,即Ai(i≠0) 独立地确定向Rk发送的数据量大小. Ai(i≠0) 向A0发送的总的数据量si一定,由用户的需求决定,其为发送到A0各个边缘路由流量的和,即
|
图 2 A0的入流量规划模型 |
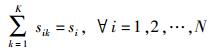
|
(1) |
对于A0的任意一个边缘路由Rk,其收到的入流量为所有其他自治域通过Rk发送到A0的流量和,即
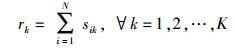
|
(2) |
Rk(k=1, 2, …, K)在收到数据流后,根据数据流的目的地址和域内路由协议通过其域内链路传输到不同的域内路由.不失一般性,假设Rk收到的外部流量的目的地址均匀分布在其域内路由器中,则每个内部链路l只与rk(k=1, 2, …, K)有关.用函数cl=gl(r1, …, rK)表示流经链路l的数据流量,若A0的链路带宽为C,则链路l的负载为
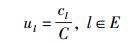
|
(3) |
其中E为A0链路的集合.反映流量规划性能的指标主要有最大链路利用率和网络开销.前者反映自治域最拥塞链路的负载,后者反映网络的整体负载状况.考虑流量规划与ISP收益的关系,而ISP的收益和网络整体的拥堵状态相关,因此以网络开销作为评价指标.具体而言,链路l(l∈E)的负载ul被单调递增的凸函数f映射为“链路开销”.随着负载u的增加,链路开销f(u)非线性地增加,表示该链路的拥塞程度非线性地增加. f的具体形式和用户需求相关,一种根据实际数据测量得到的f[4]为
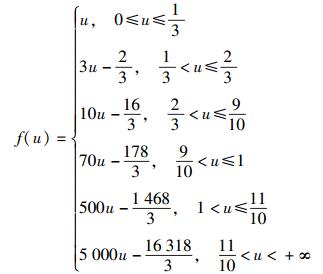
|
(4) |
“网络开销”θ为自治域链路开销的和,即

|
(5) |
网络开销θ反映了自治域整体的流量规划的性能.由于链路的负载是入流量的函数,则θ也为入流量r1, r2,…, rK的函数,即
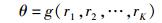
|
(6) |
θ越大,该自治域的拥塞程度越高,数据流在该自治域的传输时延越大,其由于拥塞导致的时延增加远远超过网络的传输时延,成为网络性能的瓶颈.
网络拥塞的程度对ISP的收益有巨大的影响.一方面,ISP的网络拥塞程度直接影响到其域内的内容运营商(CP, content provider)为用户提供的服务质量.例如,百度、亚马逊等CP对数据包从数据中心到达用户的时延有严格要求,并不断进行优化,以期提高用户服务质量.如果ISP提供的网络出现拥塞,CP无论如何优化其数据中心的效率,都难以保证用户的服务质量,从而影响CP和ISP的运营效率和收益.另一方面,ISP的网络拥塞程度影响用户的忠诚度.一个区域往往存在多个ISP,若某个ISP的网络拥塞程度较高,则用户倾向于向其他ISP购买网络接入服务.
用ϕ表示当前某种网络拥塞程度θ对应的ISP收益,如式(7) 所示. ISP的收益随着网络拥塞程度下降(或不增长),因此U是θ单调不减的函数.定量分析网络拥塞对ISP收益的影响不在笔者的研究范围内,ϕ的具体形式与网络流量、CP的服务质量和用户需求有关.
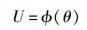
|
(7) |
根据式(6),θ由A1, A2, …, AN共同决定.根据式(7),A0的收益U也由A1, A2, …, AN共同决定.考虑A0与A1, A2, …, AN合作形成联盟,降低A0的拥塞程度θ,从而提高A0的收益U. U的增益则根据参与联盟的自治域的贡献进行分配.用联盟博弈[5]建立模型,考虑联盟Λ={A0, A1, …, AN},若v表示联盟的收益,则联盟的目标函数为
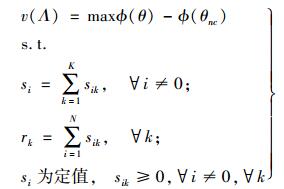
|
(8) |
其中ϕ(θnc)为非合作情况下A0的收益,为定值.式(8) 的目标函数是最大化A0收益的增加.第1个约束保证Ai传输到A0的总流量需求得到满足.第2个约束为Rk的入流量,是Ai(i≠0) 发送的流量总和.联盟的目标是通过自治域Ai(i≠0) 改变sik最大化v(Λ).
2.2 联盟的核心最大化v(Λ)并不一定需要所有加入联盟的边缘自治域都修改求流量sik.对于任意一个联盟,核心用来表示实现该联盟利益最大化的稳定的最小集合,即核心内的任何自治域都能为联盟的优化目标提供增益,且其在该核心内同时实现自身利益的最大化.具体到文中场景,若c(Λ)为Λ的核心,则c(Λ)的定义为
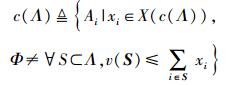
|
(9) |
其中:X(c(Λ))为c(Λ)的利益分配方式,xi为Ai在c(Λ)内的收益,v(S)为联盟Λ的子集合S的总收益. 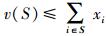
1) c(Λ)一定包含A0.根据式(8),v(S)完全是由优化A0的入流量得到的.若c(Λ)不包含A0,则A1, A2, …, AN不能使v(S)增加.因此c(Λ)一定包含A0,即A0∈c(Λ).
2) 若c(Λ)为空集,则v(Λ)达到最优.用反证法:若c(Λ)为空集且v(Λ)没有达到最优值,则存在Ai(i=1, 2, …, N)能增加v(Λ),即能通过降低θ提高ϕ(θ),则{Ai(i=1, 2, …, N), A0}满足核心的定义,与c(Λ)为空集矛盾,即证.
3) 联盟的核心c(Λ)不唯一.根据式(6) 所示,θ是入流量r1, …, rK的函数.又如式(2),对于A0的某个边缘路由器的入流量rk,其增大或减小由sik(∀i≠0) 共同决定.因此,当Ai∈c(Λ)、Aj∉c(Λ),且Ai在核心中转移的流量能被Aj替代时,则令Aj替换Ai仍然能实现v(Λ)的最大化.本质上,c(Λ)不唯一的原因是A0的入流量规划依赖于分配在其边缘路由器的流量大小,而不依赖于分配在某个边缘路由器的流量是由哪个边缘自治域(Ai(i≠0))提供的.
2.3 核心的求解联盟的核心并不唯一,因此可能存在很多个边缘自治域的组合,使得v(Λ)最大.但在实际情况中,考虑到向A0发送数据的边缘自治域数目较多(N较大),而更多自治域的合作过程往往可能带来其他开销(切换链路增加的路由表项等),希望选取最少的边缘自治域数目与A0形成联盟的核心.
令ai, kp(∀i≠0, k, p=1, 2, …, K)表示Ai从A0第k个边缘路由Rk转移到第p个边缘路由Rp的流量,则由流量守恒有
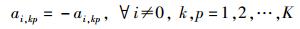
|
(10) |
对于联盟的目标函数v(Λ)(式(8)),其为网络开销θ的函数.由式(6) 可知,θ为A0分配在每个边缘路由的入流量的函数.因此,v(Λ)也为A0分配在每个边缘路由器的入流量的函数.根据A0的拓扑和域内路由协议,可以求得当v(Λ)最大时A0边缘路由器的入流量r1*,…, rK*.在未进行联盟时,其每个边缘路由器的入流量分别为r1, nc,…, rK, nc,则需要调整的入流量可以表示为式(11) 求解.
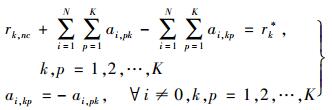
|
(11) |
其中,第1个方程表示A0的任意一个边缘路由的入流量变化最终达到满足v(Λ)的最大值;第2个方程表示Ai(i≠0)Rk的流量调整是守恒的.若Ai(i≠0)∈c(Λ),根据联盟定义,其一定转移流量以提高v(Λ).用bi表示Ai(i≠0) 是否转移了流量,则
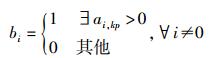
|
(12) |
因此求解联盟的核心可以表示为整数规划问题,如式(13) 所示.整数规划属于NP难问题,可以采用CPLEX、LINGO等优化软件求解.
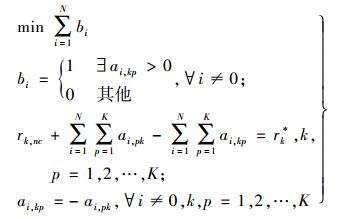
|
(13) |
联盟的核心c(Λ)能实现联盟优化目标v(Λ)的最大化. v(Λ)是由于入流量规划所产生的A0运营收益的提高.这些收益来自于加入c(Λ)通过合作实现,因此需要按照一定的规则将v(Λ)分配给Ai∈c(Λ).最经典的分配方式是通过SHAPLEY值进行分配,即按照参与者在联盟博弈的贡献为其分配收益.
假设有Na个边缘自治域形成联盟的核心,不失一般性,表示为c(Λ)={A0, A1, …, ANa-1}.若令xi(i=0, …, Na-1) 表示分配给Ai的收益,则分配收益的总和与核心获得的收益相同,即
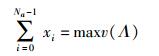
|
(14) |
同时,收益的分配满足可交换性,即∀i∈S, ∀j∉S, S⊂Λ,v(S/{i}∪{j})=v(S).满足上述条件的收益可以用SHAPLEY值计算,则
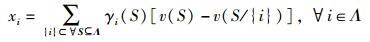
|
(15) |
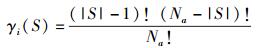
|
(16) |
其中:|S|为子联盟S参与者的数目;v(S/{i})为子联盟S除去Ai的收益,即Ai的边际贡献;xi(i=0, 1, …, Na-1) 为Ai在核心的任意子集S的边际贡献的加权和.
4 仿真实验考虑A0和6个边缘自治域基于联盟博弈的入流量规划,每个边缘自治域有2个边缘路由的典型场景.使用Abilene[6]和CERNET[7]2个网络拓扑作为仿真拓扑.对于Abilene拓扑,把DNVY和KSCY作为2个边缘路由.对于CERNET拓扑,把青岛和上海作为2个边缘路由.域内的路由协议为最短路径,域内链路权重和选用的拓扑一致[6-7].边缘自治域的链路带宽为10 Gbit/s.假设6个自治域随机地将5 Gbit/s的数据随机发送给A0的2个路由器,进行100次仿真统计其概率累积分布.
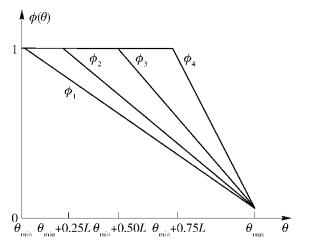
考虑到收益函数与拓扑有关,把性能最优的入流量规划所产生的收益定义为v(S)=1,性能最低的入流量规划所产生的收益定义为v(S)=0.函数ϕ反映了收益与入流量规划的性能以及收益对入流量规划性能的变化程度.选取4种ϕi(i=1, 2, 3, 4),如图 3所示(其中L=θmax-θmin). ϕ1为线性函数,表示A0的收益随着θ线性减少. ϕ2、ϕ3、ϕ4为分段函数,分别在θmin和θmax 之间的1/4、1/2、3/4分位开始线性下降,表示收益受到网络开销影响的起始点θ逐渐增加.
|
图 3 ϕ(θ)函数表达式 |
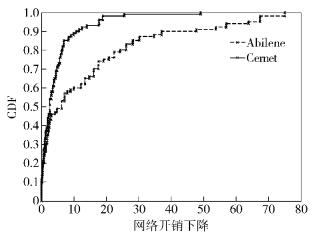
图 4为基于联盟博弈的网络开销的下降概率累积分布图.网络开销的下降和边缘自治域的拓扑图相关.相比于CERNET,Abilene网络开销下降的绝对数更高.
|
图 4 网络开销下降概率累积函数 |
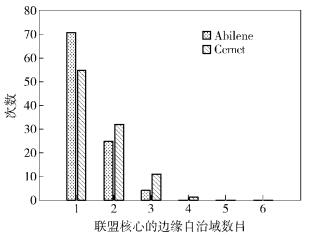
图 5示出了组成联盟核心的边缘自治域数目.虽然仿真场景为6个边缘自治域向A0发送流量,但联盟核心的数目小于5.这是因为转移A0有入流量以实现A0的负载均衡并不需要所有的外部边缘自治域都进行流量的路径转移.实际上,仿真实验中超过50%的情况只需要转移一个外部自治域的流量.
|
图 5 联盟核心的边缘自治域个数 |
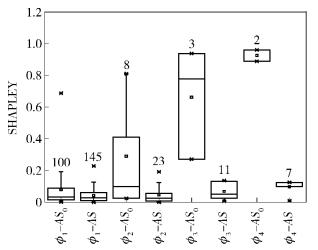
图 6以Abilene为例分析了不同的ϕ对SHAPLEY分配的影响(CERNET结论类似). ϕ1-AS0、ϕ1-AS分别表示在ϕ1下A0和Ai(i≠0) 的SHAPLEY值.每个箱式图标注了最小值、1/4分位、1/2分位、3/4分位和最大值.箱式图上方的数字表示在100次仿真中自治域合作的次数.随着ϕ1~ϕ4,A0收益下降的网络开销门限逐渐增大.因此随着ϕ1~ϕ4,产生联盟的次数越来越少.同时,一旦收益随网络开销的增大下降,其斜率增大.然而也因此,其合作带来的收益的增加值增大.即一旦出现网络开销的下降,则合作的收益增益更大.
|
图 6 ϕ对联盟自治域收益的统计值 |
在骨干边缘分离网络架构下分析了自私性导致的边缘网入流量不均衡的问题,提出了联盟博弈的入流量规划模型.该模型建立网络开销与自治域ISP收益的对应关系,通过联盟博弈实现边缘自治域网络开销的降低和ISP收益的提高.提出了核心的计算方法和基于SHAPLEY值的收益分配方法.仿真结果证明,联盟博弈的效果受到拓扑、收益与网络开销函数关系、边缘自治域合作前的入流量规划性能,以及合作自治域转移的流量的影响.
| [1] | Farinacci D, Fuller V, Lewis D, et al. RFC 6830—2013, Locator/id separation protocol (LISP)[S]. IETF, 2013: 1-75. |
| [2] | Secci S, Liu K, Jabbari B. Efficient inter-domain traffic engineering with transit-edge hierarchical routing[J].Computer Networks, 2012, 57(4): 976–989. |
| [3] | Zhang Y, Wang Y, Pei D, et al. Multi-AS cooperative incoming traffic engineering in a transit-edge separate internet[J].Computer Networks, 2014, 73(1): 112–127. |
| [4] | Fortz B, Thorup M. Internet traffic engineering by optimizing OSPF weights[C]//2000 Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM 2000). Tel Aviv Israel: IEEE Press, 2000: 519-528. |
| [5] | Saad W, Han Z, Debbah M, et al. Coalitional game theory for communication networks[J].IEEE Signal Process, 2009, 26(5): 77–97. doi: 10.1109/MSP.2009.000000 |
| [6] | TOTEM Project, Abilene website[EB/OL]. Belgium: TOTEM, 2008[2014-12-26]. http://totem.run.montefiore.ulg.ac.be/datatools.html. |
| [7] | CERNET. CERNET主干网流量优化探索[EB/OL]. 2006[2014-12-26]. http://www.edu.cn/. |


