典型蔡氏电路中引入符号函数代替原有蔡氏二极管, 构建了一个能产生多涡卷混沌吸引子的变形蔡氏混沌系统模型.构造方法是使该函数中的每个平衡点分别位于相邻两个转折点的正中间, 并且保持混沌吸引子中涡卷与键带的相互间置.该模型的动力学分析和Matlab数值仿真表明, 该系统能产生10涡卷混沌吸引子.最后, 设计了硬件电路并且给出了最多10个涡卷的硬件电路实验结果.硬件实验结果与理论分析和仿真分析完全吻合, 进一步证实了该系统的存在.
A model of the modified Chua's chaotic system was constructed to produce multi-scroll chaotic attractors, replacing the typical Chua's diode with the sign function in the typical Chua's circuit. The method is to make equilibrium point located in the center of two adjacent breakpoints, and keep scrolls and bond orbits alternated with each other. Both model analysis and Matlab simulation show that the system generates 10 scrolls chaotic attractors. Finally, the design of the hardware circuit produces at a maximum of 10 scrolls hardware experimental results. Hardware experiments, analysis and simulation are almost accordance, which further proved the existence of the system.
1983年,蔡少棠提出了著名的蔡氏电路,将混沌由理论引向实际应用阶段.此后,人们还进一步提出了对偶蔡氏电路、变形蔡氏电路等形式[1-4].围绕性态复杂的多涡卷混沌系统的产生与应用成为研究的一个热点,2007年以来,Yalcin、Suykens和Vandewalle研究小组提出了使用分段线性函数等产生多涡卷混沌吸引子的方法,并且给出了最多5涡卷混沌吸引子的电路实验结果[5-6].近年来,先后有人提出用正弦函数、三角波序列、时滞函数等产生多涡卷的方法[7-13].
1 变形蔡氏多涡卷混沌系统1.1 系统构造考虑到符号函数的某些特征符合蔡氏二极管的分段特性和多涡卷产生的条件,引入符号函数f(x)代替蔡氏电路中原有蔡氏二极管,该函数中的每个平衡点分别位于相邻两个转折点的正中间,并且保持混沌吸引子中涡卷与键带的相互间置,同时对典型蔡氏电路中的参数进行修正,得到式(1) 所示的三维变形蔡氏电路的量纲为一的状态方程.
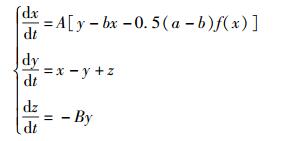
|
(1) |
其中: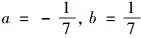
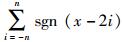
1) 对称性和不变性
提出的系统做如下变换后
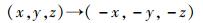
|
(2) |
系统保持不变,即系统关于原点对称,且这种对称性对所有的参数均成立.
2) 系统散度
提出的系统是一个耗散系统,系统的散度∇V为
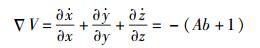
|
(3) |
提出系统的收敛速率为
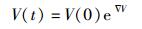
|
(4) |
因为Ab+1>0,所以提出的系统是耗散的.当t→∞时,包含系统轨线的每个体积元都以指数率-(Ab+1) 的速度收缩,初始体积元V(0) 的体积元在时间t时收缩为体积元V(0) e-(Ab+1),即一个吸引子上.
3) 平衡点
下面以产生10涡卷混沌吸引子为例,f(x)= 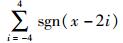
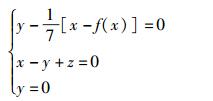
|
(5) |
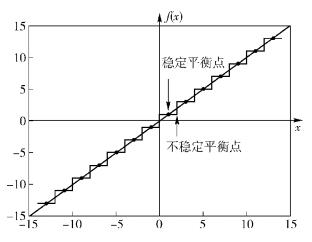
考查式(5),系统的平衡点即为h(x)=x-f(x)的零点,h(x)零点如图 1所示.
|
图 1 系统的平衡点图解 |
显然在x∈(2i, 2i+2) 区间内,f(x)是连续的,系统的平衡点落在(2i, 2i+2) 区间内.由图 1可知,稳定平衡点就是符号函数的阶梯型图形与直线x=f(x)的交点ei=2i+1.此外,图 1中还有跳跃点,即系统的不稳定平衡点ei=2i.由图 1可知,在x∈(-14, 14) 区间内,h(x)满足在每个连续(2i, 2i+2) 区间内有且只有有限个第一类间断点,并且至多只有有限个极值点.
根据傅里叶级数收敛定理可知,h(x)的傅里叶级数收敛,并且当x是h(x)的连续点时,级数收敛于h(x);当x是h(x)的间断点时,级数收敛于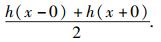
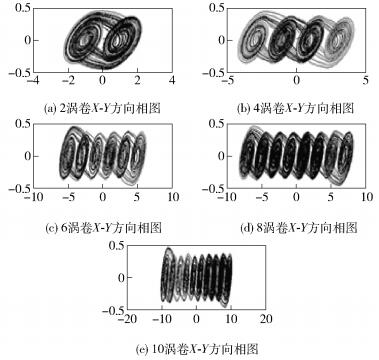
对式(1) 系统采用龙格-库塔法积分,时间长度T=(0,800),初始值{x, y, z} = {0.01,0.02,0.03}. Matlab仿真结果如图 2所示. 图 2(a)~(e)分别为2、4、6、8、10个涡卷X-Y方向相图.仿真结果表明,该系统可以产生多涡卷混沌吸引子.
|
图 2 2~10偶数个涡卷混沌吸引子的Matlab仿真结果 |
以产生10涡卷为例,根据模块化电路设计思想,对式(1) 进行微分-积分变换,得到
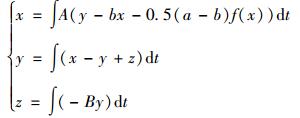
|
(6) |
根据式(6),设计出如图 3所示的电路.整个电路由两部分构成,图 3(a)为基本蔡氏电路,整个电路由反相加法器、积分器和反相器3个模块构成;图 3(b)为符号函数产生电路.
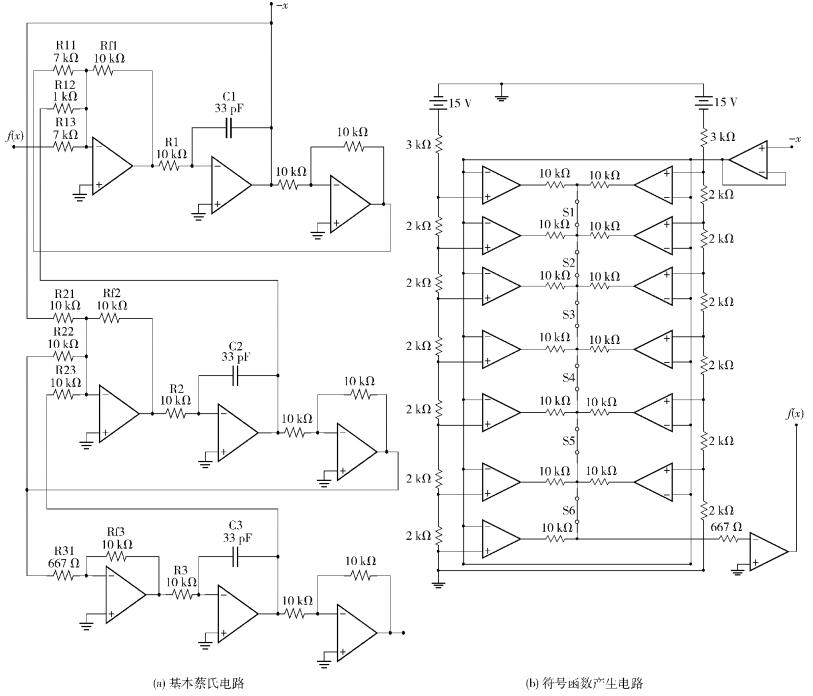
|
图 3 硬件电路 |
对图 3所示电路进行硬件实验可得如图 4所示的实验结果.该实验结果是通过数码相机从模拟示波器上获得的.
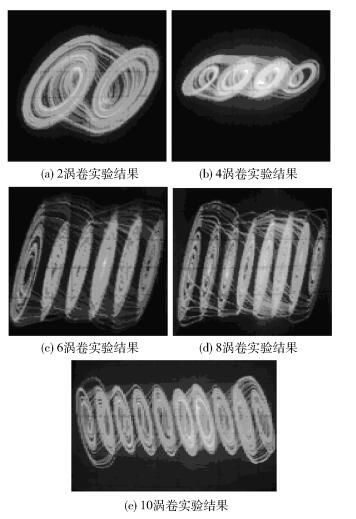
|
图 4 硬件电路实验结果 |
构建了一个利用符号函数代替原有蔡氏二极管的新混沌系统,该系统能产生多涡卷.它区别于利用正弦波函数、三角波序列、时滞函数产生多涡卷的方法.该方法使得涡卷与键带之间保持相互间置,更易于产生多涡卷.以10涡卷为例,给出了Matlab仿真结果,并设计了硬件电路和进行了相应的硬件实验.硬件实验结果与理论分析和仿真结果完全吻合,证实了该系统不仅是一个多涡卷混沌系统,而且是物理可实现的系统.值得注意的是,给出了最多10个涡卷的硬件电路实验结果,该实验结果是目前不可多得的实验成果.有关从蔡氏电路中获取更多个涡卷的问题,将做进一步的研究.
| [1] | Viana E R, Rubinger R M, Albuquerque H A, et al. Periodicity detection on the parameter-space of a forced Chua's circuit[J].Nonlinear Dynamics, 2012, 67(1): 385–392. doi: 10.1007/s11071-011-9986-5 |
| [2] | Manimehan I, Thamilmaran K, Philominathan P. Torus breakdown to chaos via period-3 doubling route in a modified canonical Chua's circuit[J].International Journal of Bifurcation and Chaos, 2011, 21(7): 1987–1998. doi: 10.1142/S0218127411029586 |
| [3] | Ahamed A L, Srinivasan K, Murali K, et al. Observation of chaotic beats in a driven memristive Chua's circuit[J].International Journal of Bifurcation and Chaos, 2011, 21(3): 737–757. doi: 10.1142/S0218127411028763 |
| [4] | Marszalek W, Trzaska Z. Mixed-mode oscillations in a modified Chua's circuit[J].Circuits Systems and Signal Processing, 2010, 29(6): 1075–1087. doi: 10.1007/s00034-010-9190-8 |
| [5] | Yalcin M E. Multi-scroll and hypercube attractors from a general jerk circuit using Josephson junctions[J].Chaos Solitons Fract, 2007, 34(5): 1659–1666. doi: 10.1016/j.chaos.2006.04.058 |
| [6] | Kilinc S, Yalcin M E, Ozoguz S. Multiscroll chaotic attractors from a hysteresis based time-delay differential equation[J].Int J Bifurcat Chaos, 2010, 20(10): 3275–3281. doi: 10.1142/S0218127410027660 |
| [7] | Suzuki M, Sakamoto N. Controlling ideal turbulence in time-delayed Chua's circuit: stabilization and synchronization[J].International Journal of Bifurcation and Chaos, 2010, 20(5): 1351–1363. doi: 10.1142/S0218127410026526 |
| [8] | Tuerk M, Ogras H. Recognition of multi-scroll chaotic attractors using wavelet-based neural network and performance comparison of wavelet families[J].Expert Systems with Applications, 2010, 37(12): 8667–8672. doi: 10.1016/j.eswa.2010.06.063 |
| [9] | Sun Guanghui, Wang Mao, Huang Lilian, et al. Generating multi-scroll chaotic attractors via switched fractional systems[J].Circuits Systems and Signal Processing, 2011, 30(6): 1183–1195. doi: 10.1007/s00034-011-9272-2 |
| [10] | Turk M, Gulten A. Modelling and simulation of the multi-scroll chaotic attractors using bond graph technique[J].Simulation Modelling Practice and Theory, 2011, 19(3): 899–910. doi: 10.1016/j.simpat.2010.12.003 |
| [11] | Bouallegue K, Chaari A, Toumi A. Multi-scroll and multi-wing chaotic attractor generated with Julia process fractal[J].Chaos Solitons and Fractals, 2011, 44(1): 79–85. |
| [12] | Carbajal V H, Tlelo E, Fernandez F V. Optimizing the positive Lyapunov exponent in multi-scroll chaotic oscillators with differential evolution algorithm[J].Applied Mathematics and Computation, 2013, 219(15): 8163–8168. doi: 10.1016/j.amc.2013.01.072 |
| [13] | Munoz P, Jesus M, Zambrano E, et al. Synchronization of PWL function-based 2D and 3D multi-scroll chaotic systems[J].Nonlinear Dynamics, 2012, 70(2): 1633–1643. doi: 10.1007/s11071-012-0562-4 |


