2. 上海理工大学 光电信息与计算机工程学院, 上海 200093
由于Internet具有动态特性, 使得Internet尽力而为的服务模式在传输群组命令时, 容易产生无效(过期)路径.对此, 提出群组动态遗传算法.该算法分别从静态搜索和动态搜索两个角度考虑无效(过期)路径问题.其主要优势在于解决传统遗传算法在动态环境下无法收敛问题.实验验证了该算法相对于当前一些经典算法在支持群组命令传输方面具有较好的性能.
2. School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China
The problem of path invalid or path expired caused by best-effort model transmitting of groups commands under continuously changed Internet parameters comes into notice recently. A new group dynamics genetic algorithm was proposed. The algorithm takes into account the problem from static search and dynamic search. The advantage of the algorithm is keeping astringency short of traditional genetic algorithm. Experiments show that the performance of the algorithm is better than the used algorithms.
物联网核心思想是不仅“感知”而且期待“可控”.物联网运营中心作为“可控”关键技术已经成为当前研究热点[1].其主要功能是通过Internet实时地传输一组具有约束的控制命令到不同区域的终端设备,并且这组控制命令必须在满足约束条件下全部到达指定区域的终端设备,任何单一控制命令传输丢失都被视为传输失败.然而Internet尽力而为的服务模式并不支持群组命令传输.其主要原因是Internet具有动态特性,尽力而为的服务模式在动态环境下容易产生路径无效(过期),最终使得群组命令传输失败.为解决这些问题,研究基于Internet的群组命令传输过程(GCT,group command transmission)的有效性问题.
当前,基于Internet的GCT研究较少[2]. Shier[3]提出了求第K条最短路径的算法二重扫除法(DSA,double-sweep algorithm),只要图中不含负回路DSA计算非常有效. Yen[4]定义了一种基于精确参数的第K条最短无环路由Yen算法,但K最优路径算法[3-4]没有考虑Internet动态变化对算法的影响;而且K最优路径算法主要针对单源-目的节点对之间的多条路径选择过程,并不适合GCT. IPv6(Internet protocol version 6) 组播技术是下一代Internet研究重心[5],然而其在支持GCT方面,依然存在困难:1) IPv6组播中身份认证机制不适用于GCT;2) IPv6组播技术基于组播树复制技术转发,而GCT中每个控制命令都是独立的,不能通过复制技术转发.
对此,通过在Internet上植入部分通信代理节点(CSA,communication service agent),使得CSA构建物联网运营中心所涉及的Internet局部区域的骨干网络,也即有效路径统计网络(EPSN,effective path statistics network).该网络主要功能是实时测量与统计CSA之间逻辑链路上的度量参数,并基于测量结果构建有效路径集用于支持GCT.构建EPSN主要优势在于,有效减少Internet动态变化对GCT的影响.
将基于Internet的GCT问题转换为基于EPSN的GCT问题.由于每个单一命令传输过程可以看成多约束多目标优化问题(MCMOOP,multi-constraints multi-objectives optimization problem),则把基于EPSN的GCT问题转换为基于EPSN的群组多约束多目标优化问题(GMCMOOP,group multi-constraints multi-objectives optimization problem).
1 问题描述设EPSN表示为G=(V, E, t),其中V为CSA集合,E为CSA之间链路集合,t为时间.每条链路e∈E上都拥有一组参数j(j=1, 2, …, n),且j与时间t有关,给定一组参数约束值Cj(j=1, 2, …, n),则有
基于EPSN的MCMOOP描述为:在时间t内以及子参数目标函数满足约束条件下,寻找一组非劣解x(或有效路径),使得MCMOOP目标函数最优(在此定义最大为最优),即
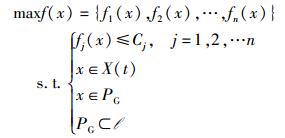
|
(1) |
其中:x为非劣解(或有效路径),f(x)为MCMOOP目标函数,fj(x)(j=1, 2, …n)为子参数目标函数,X(t)为随时间变化函数,PG为非劣解集,
基于EPSN的GMCMOOP描述为:在时间t内以及满足群组约束条件下,寻找多组非劣解集PG1, PG2, …, PGn,对每组非劣解集PGj(j=1, 2, …, n)使其对应多目标优化函数最优,同时使得GMCMOOP目标函数最优,即
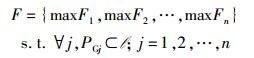
|
(2) |
其中:Fj(j=1, 2, …, n)为第j个MCMOOP,F为GMCMOOP目标函数.
可知,讨论的GMCMOOP属于组合优化问题.传统的遗传算法在解决组合优化问题上具有较好的性能[6],但是其在动态环境下会造成无法收敛问题.因此,借鉴武燕等[7]的思想,提出群组动态遗传算法.该算法优势在于,在动态环境下能时刻追逐最优解并且能快速收敛,从而克服传统遗传算法无法收敛的可能.以下将对群组动态遗传算法进行详细描述.
2 群组动态遗传算法2.1 群组动态遗传算法参数及规则设置每个个体编码方式:为了简化算法,群组动态遗传算法(GDGA,group dynamics genetic algorithm)采用二进制编码方式.
选择规则:假设群体规模为N,对于个体i的适应度值为zt(i),则个体i适应度比例为
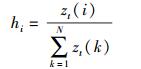
|
(3) |
则对于个体i而言,被选择概率bi为
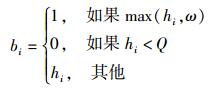
|
(4) |
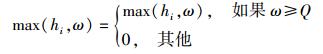
|
(5) |
其中:Q∈(0, 1) 为变量,max(hi, ω)为在变量参数ω满足一定范围内最大的适应度比例函数,ω∈(0, 1) 为变量参数.
交叉规则:采用基于竞争退让的多点交叉思想,设置交叉参数δ,且
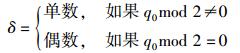
|
(6) |

|
(7) |
其中:l为冲突次数,q0为竞争避让参数.在第j次迭代过程中,单点交叉和双点交叉同时随机产生q0值,如果同为单数或双数则表示冲突.当不发生冲突时,随机选取q0;当发生冲突时,双方一直随机产生q0,直到不发生冲突为止.如果δ为单数,则采用单点交叉思想,随机取交叉点,然后根据单点交叉思想进行处理;如果δ为偶数,则采用双点交叉思想,随机取2个交叉点,然后根据双点交叉思想进行处理.
变异规则:采用轮盘逆转变异思想,在个体二进制码串中根据轮盘思想选择1个逆转点,然后将原点与逆转点间或逆转点与终点间的码串以pI进行逆向排序,则
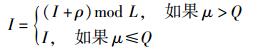
|
(8) |
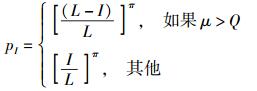
|
(9) |
其中:π(π≥1) 为参数,I为逆转点的下标,L为二进制码串总长度,ρ(ρ≥1) 为随机常数,μ∈(0, 1).
2.2 GDGA搜索策略分析2.2.1 静态搜索过程如果在时间t内,解空间中解并没有随时间变化而发生动态变化.在这种情况下,可以看成静态搜索过程,参考传统遗传算法搜索思想即可.
2.2.2 动态搜索过程由于Internet具有动态变化特性,因而解(有效路径)会随时间变化而时刻动态变化.假设在t1时刻搜索到的解为最优解,但是在t2时刻其发生变化,意味着遗传算法在t1时刻搜索到的最优解已经失效.解动态变化过程如图 1所示.

|
图 1 解动态变化示意图 |
图 1中,小黑点表示搜索到的解,x坐标和y坐标分别表示所对应的度量参数(为了方便只讨论2个度量参数),t坐标表示时间轴.由图 1可知,在t1时刻搜索到的解,在t2时刻时其位置相对于在t1时刻的位置发生了动态迁移,因而造成路径过期或路径无效.
动态搜索思想:在空间中搜索解过程时,每个个体i根据解迁移(ST,solution transfer)策略探测其当前位置上的解是否随时间变化而导致位置发生变化.其中,ST策略由更新触发函数和触发规则组成.
更新触发函数g(x, t)理解为解x在t时刻重要且已经长时间没有更新,则触发的可能性较大,且
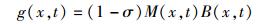
|
(10) |
其中:g(x, t)∈(0, 1) 为解x在时刻t更新触发函数,σ∈(0, 1) 为参数,M(x, t)∈(0, 1) 为解x在时刻t重要度,B(x, t)∈(0, 1) 为解x在时刻t时距离上次更新间隔程度,同时触发规则可以定义为
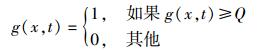
|
(11) |
其中:1表示g(x, t)触发,0表示g(x, t)不触发.
如果探测到解变化,则在当前位置上的个体i根据随机生成数函数生成一个动态标识位,接着个体i根据动态标识位,对自身位取反生成动态个体j,进一步假设R表示为半径,且
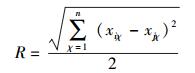
|
(12) |
其中xiχ、xjχ分别为个体i和动态个体j在空间坐标中的第χ个分量,同时构建以个体i与动态个体j空间连接线的中心点为圆心,R为半径的动态搜索区域.最后,在该区域中随机产生一组个体i虚拟个体组取代个体i,并依然根据静态或者动态搜索过程搜索,一直到算法搜索到有效时间内非劣解或条件满足为止.
2.3 GDGA实现步骤1 分解GMCMOOP为一组MCMOOP.对于每个MCMOOP,初始化解空间、各类参数,设置迭代次数τ,创建数组变量U,确定种群规模为N,并根据均匀划分思想,划分整个搜索空间,然后均匀分布种群及初始化其适应度函数,且每个个体的编码方式基于二进制编码,转入步骤2.
步骤2 首先对每个个体,根据解ST及式(10)(11) 判定其属于静态搜索或动态搜索.如果属于动态搜索,则根据式(12) 均匀产生一组虚拟个体代替当前个体;如果属于静态搜索,则不需扩展当前个体.接着,分别计算每个个体(包括扩展后的个体)所对应的适应度并排序,转入步骤3.
步骤3 根据选择规则以及式(3)~式(5) 进行个体选择操作,转入步骤4.
步骤4 根据交叉规则以及式(6)(7) 进行个体交叉操作,转入步骤5.
步骤5 根据变异规则以及式(8)(9) 进行个体变异操作.经过选择、交叉和变异等操作后,变量U记录当前最优解(或有效时间内最优解),转入步骤6.
步骤6 为保持解的多样性,借鉴小生境思想更新数组变量U,如果τ不满足条件,则转入步骤2;否则,转入步骤7.
步骤7 如果所有的MCMOOP已经达到结束条件,则转入步骤8;否则,一直等待.
步骤8 记录所有MCMOOP的解U,则为GMCMOOP的解,退出.
3 实验与分析实验环境配置:曙光集群20个服务器,每个服务器配置CPU为AMD皓龙4122,内存4 GB,硬盘300 GB,操作系统为SUSE Linux Enterprise Server 11.
参数设置:Q∈(0.85, 0.95),τ∈(500, 1 000),N∈(100, 150).
网络拓扑结构:利用Waxmam模型[8]随机生成的网络拓扑结构.其中,随机网络拓扑结构具有20个节点,22条链路,并在每条链路上随机产生n个度量参数,n≥2,链路上度量参数值随机产生,同时每个度量参数约束随机产生,平均节点度小于7.
网络部署:根据Waxmam随机产生的网络拓扑结构在Internet下,部署20个曙光服务器(CSA节点),构建成EPSN,并且运行GDGA.
EPSN动态环境设置:在Internet环境下,通过在不同的时间间隔内不断随机改变EPSN规模,改变EPSN规模包括增加或减少当前节点以及节点之间的逻辑链路等.
实验1 在群体命令规模最小值80和最大值310的条件下,基于EP集验证GDGA与当前一些经典算法之间的群体命令传输成功率性能比较:
群体命令传输成功率=群体命令传输成功数/群体命令传输总数
群体命令规模在最小值80和最大值310情况下,测试各种算法传输成功率.
图 2中,横坐标表示EPSN规模,纵坐标表示传输成功率.当EPSN规模为5~10个时,GDGA传输成功率接近82%,DSA传输成功率接近79.3%,Yen算法传输成功率接近79.3%,GDGA传输成功率相对于DSA和Yen算法分别提高了3.4%和3.4%;当EPSN规模为15~20个时,GDGA传输成功率接近91.3%,DSA传输成功率接近87.95%,Yen算法传输成功率接近87.3%,GDGA传输成功率相对于DSA和Yen算法分别提高了3.8%和4.58%.
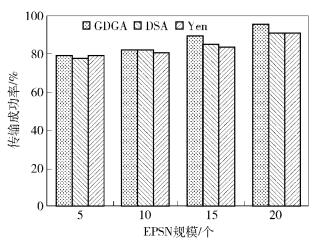
|
图 2 Internet下群体命令规模80传输成功率 |
图 3中,横坐标表示EPSN规模,纵坐标表示传输成功率.当EPSN规模为5~10个时,GDGA传输成功率接近67.1%,DSA传输成功率接近54.5%,Yen算法传输成功率接近54.25%,GDGA传输成功率相对于DSA和Yen算法分别提高了22.9%和23.6%;当EPSN规模为15~20个时,GDGA传输成功率接近86.1%,DSA传输成功率接近75.4%,Yen算法传输成功率接近74.2%,GDGA传输成功率相对于DSA和Yen算法分别提高了14.1%和16.03%.
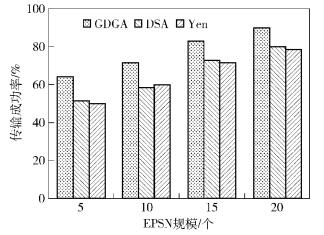
|
图 3 Internet下群体命令规模310传输成功率 |
以上分析可知, GDGA在网络结构相对稳定环境下性能较好,同时随着GCT规模增大其性能会降低,随着EPSN规模扩大会有效增加GDGA性能.
实验2 在动态环境下,通过非劣解的误差率验证GDGA与传统遗传算法(GA,genetic algorithm)寻找全局最优解的能力.其中:
解的误差率=|实际的解-计算的解|/实际的解
图 4中,横坐标表示EPSN规模数,纵坐标表示误差率.当EPSN规模为5~10个时,GDGA解的平均误差为2.05%,GA解的平均误差为2.55%,误差率降低了19.6%;当EPSN规模为15~20个时,GDGA解的平均误差为0.53%,GA解的平均误差为0.94%,误差率降低了43.6%.
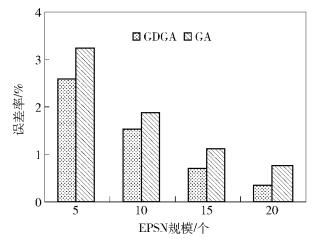
|
图 4 误差率分析 |
实验2表明,在动态环境下,GDGA比传统GA更加能有效找到最优解.
4 结束语提出一种GDGA.该算法有效解决了动态环境下GCT.通过实验进一步证明了该算法相对当前一些经典算法有较好性能.但是,该算法并没有考虑群体命令传输失败后的重传机制.因此,未来工作重点将考虑群组命令在传输失败后重传机制.
| [1] |
孙其博, 刘杰. 物联网:概念、架构与关键技术研究综述[J]. 北京邮电大学学报, 2010, 33(3): 1–9.
Sun Qibo, Liu Jie. Internet of things: summarize on concepts, architecture and key technology problem[J].Journal of Beijing University of Posts and Telecommunications, 2010, 33(3): 1–9. |
| [2] | Liu Qiang. Key technologies and applications of internet of things[J].Computer Science, 2010, 37(6): 1–4. |
| [3] | Shier D. Iterative methods for determining the k shortest paths in a network[J].Networks, 1976, 6(3): 205–229. doi: 10.1002/(ISSN)1097-0037 |
| [4] | Yen J Y. Finding the k shortest loopless paths in a network[J].Management Science, 1971, 11(17): 712–716. |
| [5] |
吴建平, 李星, 崔勇. 4Over:基于非显式隧道的IPv4跨越IPv6互联机制[J]. 电子学报, 2006, 34(3): 454–458.
Wu Jianping, Li Xing, Cui Yong. 4Over: IPv4 network interconnection over IPv6 backbone without explicit tunneling[J].Acta Electronica Sinica, 2006, 34(3): 454–458. |
| [6] |
戴晓辉, 李敏强, 寇纪淞. 遗传算法理论研究综述[J]. 控制与决策, 2000, 15(3): 263–270.
Dai Xiaohui, Li Mingqiang, Kou Jisong. Survey on the theory of genetic algorithms[J].Control and Decision, 2000, 15(3): 263–270. |
| [7] |
武燕, 刘小雄. 动态多目标优化的预测遗传算法[J]. 控制与决策, 2013, 28(5): 677–682.
Wu Yan, Liu Xiaoxiong. Predictive multiobjective genetic algorithm for dynamic multiobjective optimization problems[J].Control and Decision, 2013, 28(5): 677–682. |
| [8] | Waxman B M. Performance evaluation of multipoint routing algorithms[C]//Proceedings of the IEEE INFOCOM'93 Conference. San Francisco, USA: IEEE Computer Society, 1993: 980-986. |


