基于特征点自动匹配的图像配准技术通常无法实现亚像素精度的配准, 在多模态图像集上甚至无法完成整像素配准.为了提高多模态图像配准精度, 对亚像素图像配准技术进行研究, 提出了一种基于人工交互的适用于多模态图像的亚像素配准算法.对待配准图像和参考图像输入控制点, 利用投影变换和最小线性平方差算法进行粗配准, 根据双边平均配准误差对控制点进行亚像素调整, 从而达到精确配准.定性与定量实验结果表明, 相比基于尺度不变特征和局部强度不变的特征描述符配准算法, 该算法具备更高的配准精度, 可显著提高多模态图像配准性能.
Image registration based on key-point mappings usually provides alignment of integer-pixel precision. Sub-pixel registration is of great challenge to the technique exploiting key-point mappings. The authors proposed an interactive algorithm to address the sub-pixel registration problem. The proposed algorithm comprises two steps, the first step is to input control points and is getting a rough registration by using projection transform and linear least square algorithm, the second step is to adjust the control points with sub-pixel step. The average distance of control points was applied to quantitatively measure registration quality. The evaluation method combined with subjective and objective judgment was used. Experiment shows that the proposed algorithm can achieve sub-pixel registration result. The performance will be more reliable than other registration technique using scale invariant feature transform and partial intensity invariant feature descriptor, and also the performance of multimodal image registration gets significantly improved.
图像配准[1]是将2幅或多幅含有相同场景或目标的图像进行几何校准的过程,是三维重建、全景拼接和超分辨率的基础,广泛应用于军事、航天、医学、智能交通等诸多领域.现有配准算法分为自动配准技术和人工交互配准技术.自动配准技术从2幅图像检测特征点,匹配特征点,根据特征点匹配计算图像之间的变换关系,特征点匹配准确度是影响配准的重要因素.基于尺度不变特征(SIFT,scale invariant feature transform)配准算法[2]为单光谱图像设计,在多光谱数据(例如可见光-红外)上无法实现鲁棒匹配.在SIFT基础上提出改进对称SIFT(ISS,improved symmetric-sift)[3]和局部强度不变的特征描述符(PIIFD,partial intensity invariant feature descriptor)[4]配准方法,通过降低特征点描述符的可区分性来提高多光谱特征点匹配比例,但限于描述符无法描述多光谱图像全局信息,导致ISS与PIIFD在多光谱图像上建立的特征点匹配错误率仍然过高.从已发表的文献看,自动配准技术对多模态图像较难实现亚像素配准.人工交互图配准技术由人的视觉对待配准图像(测试图像)和参考图像进行特征点提取,利用提取到的特征点建立匹配映射变换,再将其用于测试图像,从而实现测试图像和参考图像配准.由于人的视觉在图像特征识别方面具备显著优势,相比于自动配准技术,人工交互配准的精度和准确度更高.
为了弥补自动技术在多模态图像配准上的不足,提出了一种实现人工交互的多模态图像亚像素配准方法,采用人工交互选择控制(特征)点,根据双边平均配准误差对控制点进行亚像素迭代调整,通过控制双边平均配准误差递减收敛,实现两幅图像(单模态或多模态)亚像素精确配准.实验结果表明,提出算法对多模态图像配准有较强的鲁棒性,性能优异.
1 图像配准的数学模型图像配准中作为参考的图像称为参考图像,它提供了配准操作中的参考坐标系.而目标配准图像是待配准图像,称为测试图像,通过各种变换将其坐标映射到参考图像的坐标系中,实现2幅图像在空间上的几何对齐.目前普遍采用的图像配准的数学模型描述是,在二维空间用二维矩阵表示图像,It表示测试图像,Ir表示参考图像.图像It中给定的任意像素点It(x, y),可以通过坐标变换函数M在参考图像Ir中找到相对应的点,则It和Ir图像配准问题等价于寻找最优空间变换M,满足
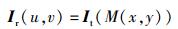
|
(1) |
其中Ir(u, v)为参考图像的像素点,使得It和Ir的几何对齐度最大,实现最佳匹配.即
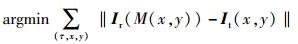
|
(2) |
其中‖·‖为二阶范数,表示测试图像映射到参考图像坐标平面后的各像素点的欧氏距离.
2 空间变换模型投影变换和仿射变换是图像配准常用并且具有一般性的2种几何变换,能在变换准确度和计算复杂度之间取得良好折中.采用投影变换设计人工交互亚像素配准方法,在算法性能评估过程中采用仿射变换.
2.1 投影变换It(x, y)通过投影变换映射为Ir(u, v),二者的坐标关系为
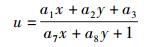
|
(3) |
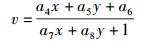
|
(4) |
设投影变换矩阵Th=[a1, a2, a3, a4, a5, a6, a7, a8],为确定Th,在It与Ir之间,至少需要4对匹配控制点对.设分别在It和Ir中输入N(N>4) 对控制点对:
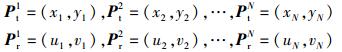
|
根据式(3) 和式(4),控制点的投影变换关系为
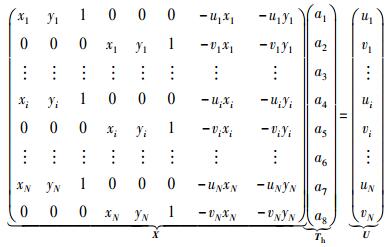
|
(5) |
当N确定时,可利用最小线性平方差方法求解式(5),获得Th的最小二乘解,在此条件下,(ui, vi)≠Th(xi, yi),但可使得N对控制点经过互相投影变换映射后的相对平均距离最小,从而实现控制点对精确匹配,提高配准性能.
根据式(5),It的控制点通过投影变换映射到Ir,与Ir的控制点的平均距离为
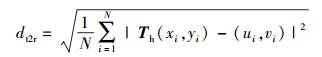
|
(6) |
根据Th的逆矩阵Th-1,Ir中的控制点通过投影变换映射到It,与It控制点的平均距离为
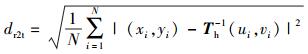
|
(7) |
dt2r和dr2t获得极值越小,则控制点对的匹配精度越高.
2.2 仿射变换利用图像仿射变换性质表征图像配准,设仿射变换矩阵为Tg, 根据仿射变换的数学定义,Tg表示为
Tg=(R,r)
其中:R是旋转矩阵,t是平移矩阵,分别表示为
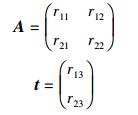
|
其中:r11、r12、r21、r22为图像的旋转系数,r13和r23为图像在水平和垂直方向的偏移量.则测试图像控制点P=(x, y)通过Tg映射为P′=(x′, y′),P和P′的关系为
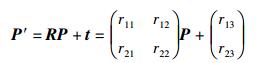
|
(8) |
基于图像特征自动配准的方法需要精确的特征提取和匹配算法,实现复杂度较高,对计算资源需求大.人工交互图配准技术由人的视觉对测试图像和参考图像进行特征点(控制点)提取.相对于自动配准算法,人工选择的控制点较易满足:1) 测试图像和参考图像初始选择的控制点特征保持一致,如同为几何特征点或角点;2) 控制点相对分散,分布相对均匀;3) 通过控制点对数目N可以在配准精度和配准效率上获得折中.提出的方法中,通过人眼识别,分别在测试图像和参考图像具备相同显著特征的控制点人工设立标记,为满足式(5),需选取超过4对控制点,利用式(5) 对控制点对进行投影变换,实现控制点对的粗匹配.
3.2 精确匹配通过式(6) 和式(7) 计算获得控制点对粗匹配的平均误差dt2r和dr2t,无法满足亚像素配准的精度要求,需要按照一定步长人工交互迭代调整控制点在测试图像和参考图像的亚像素位置,使dt2r和dr2t分别收敛于极小值,实现控制点对的精确匹配.首先设置控制点迭代调整步长s;其次按照控制点对的标记顺序,分别在测试图像和参考图像上、下、左、右4个方向上尝试移动控制点,每次移动的步长为s;然后以dt2r和dr2t取得极小值为原则搜索每对控制点对的最优匹配位置,搜索区域和方向可依据dt2r和dr2t的动态变化趋势确定;当依次遍历调整控制点对位置后,dt2r和dr2t收敛于某一区间,则测试图像和参考图像的控制点对坐标即为精确配准位置,迭代过程结束.
实验结果表明,当dt2r和dr2t分布在(0.3,0.5) 之间,N取6或7时,控制点对的配准效果较好.
3.3 算法步骤1) 初始化,设置迭代结束门限参数ε和调整步长s,提出方法设置s=0.1像素;
2) 在It(x, y)、Ir(x, y)依次人工输入N对控制点;
3) 将N对控制点坐标代入式(5),计算获得It(x, y)到Ir(x, y)的投影变换矩阵Th以及由参考图像Ir(x, y)到测试图像It(x, y)的投影变换逆矩阵Th-1;
4) 将Th和Th-1代入式(6) 和式(7),计算获得控制点对粗匹配误差dt2r、dr2t;
5) 人工调整It(x, y)、Ir(x, y)中控制点位置,调整步长为s,重新计算dt2r和dr2t;
6) 重复步骤3)、4)、5),当dt2r < ε, dr2t < ε时,人工交互迭代过程结束;
7) 利用Th,遍历It(x, y)全部像素点,构造Th(It(x, y)),将Th(It(x, y))与Ir(x, y)融合,算法结束.
4 配准性能评估方法用已知仿射变换矩阵Tg对测试图像It(x, y)进行仿射变换,获得变换后测试图像的ItTg(x, y),其所在平面设为参考平面.利用提出算法确定的匹配控制点对计算ItTg(x, y)和Ir(x, y)的仿射变换矩阵T′g,使用T′g对ItTg(x, y)进行仿射变换,则映射后像素点也位于参考平面.定义η为平均配准误差[5],则
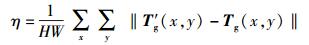
|
(9) |
其中:H为图像的高度,W为图像的宽度,单位为像素,HW表示图像的像素数目.
5 实验5.1 数据集实验数据集由9对图像构成,序号为1~9,其中图像对1为灯塔照片,1幅为近场自然可见光图像,1幅为近场红外图像,来源于Paulillsle公司网站;图像对2来自美国Landsat卫星拍摄的2011年9月英国伦敦地区洪水分布图像,1幅为可见光图像,1幅为红外图像;图像对3来自于参考文献[6],类型为人脑的核磁共振成像,1幅为PD(proton density)图像,1幅为T1WI图像(T1weighted image);图像对4、5、6、7为人工拍摄的室外可见光和红外图像;图像对8分别由Landsat8的陆地成像仪(波段:0.433~1.390 μm)和热红外传感器(波段:10.9~12.0 μm)成像;图像对9为Landsat5的成像传感器(波段:0.45~2.35 μm)在不同时间拍摄的图像.全部图像的分辨率均为384×288.
分别利用提出的方法、SIFT方法和PIIFD方法对实验图像集进行配准实验. SIFT方法采用美国加利福尼亚大学洛杉矶分校视觉源代码实现,PIIFD方法基于文献[4]实现.实验参数配置如下:
s=0.1像素,ε∈[0.3, 0.5],N=6;已知仿射变换矩阵为
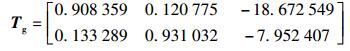
|
选取图像对1定性比较图像配准效果,图像对1由近场自然可见光和近场红外图像组成,分别利用SIFT方法、PIIFD方法和提出的方法进行特征点匹配,特征点匹配结果分别如图 1、图 2和图 3所示.由图 1可见,由于SIFT方法主要适用于单模态图像配准,对于由多模态图像构成的图像对1的特征点匹配效果较差,仅有2对特征点接近准确匹配,其他特征点对的匹配效果较差.由图 2可见,PIIFD方法确定的多模态图像特征点匹配效果尚待提高,检测的6对特征点匹配点对中,有4对正确匹配,第4对和第6对特征点存在较大偏移. 图 3表明,提出的算法确定的6对特征点对都接近正确匹配,相比图 1和图 2,图像配准更准确.

|
图 1 采用SIFT方法在图像对1上建立的特征点匹配 |

|
图 2 采用PIIFD方法在图像对1上建立的特征点匹配 |

|
图 3 采用提出的方法在图像对1上建立的特征点匹配 |
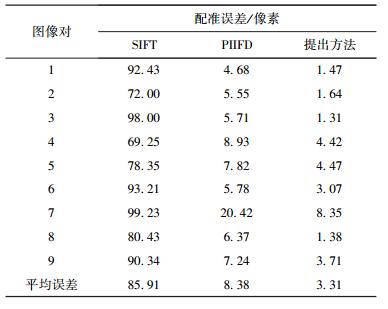
利用式(9) 对配准数据集9对图像分别计算SIFT、PIIFD和提出算法的配准误差,结果如表 1所示.
|
|
表 1 配准误差 |
误差分布如图 4所示.
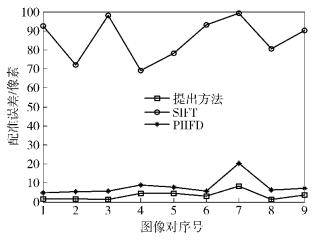
|
图 4 配准误差分布 |
定量结果表明,SIFT对多模态图像配准效果较差,对实验图像集各图像配准误差极大,平均配准误差达到85.91像素;PIIFD算法对多模态图像的配准有较好的鲁棒性,平均配准误差达到8.38像素,配准精度还需要进一步提升;提出的算法平均配准误差仅为3.31像素,配准误差优于PIIFD算法,显著优于SIFT算法,且具备较强的鲁棒性.
6 结束语亚像素配准是图像处理应用的关键问题,提出的根据配准误差人工调整控制点匹配的算法相比自动匹配算法可获得更精确的配准结果.实验结果表明,相比SIFT和PIIFD配准算法,提出算法可以提高多模态图像配准成功率,降低配准误差.
| [1] | Brown G L. A survey of image registration techniques[J].ACM Computing Surveys, 1992, 24(4): 325–376. doi: 10.1145/146370.146374 |
| [2] | Lowe G D. Distinctive image features from scale-invariant key-points[J].International Journal of Computer Vision, 2004, 60(2): 91–110. doi: 10.1023/B:VISI.0000029664.99615.94 |
| [3] | Hossain T M, Lü Guohua, Lu Guojun, et al. Improved symmetric-sift for multi-modal image registration [C]//International Conference on Digital Image Computing: Techniques and Applications (DICTA). Nossa, QLD, Australia: IEEE, 2011: 197-202. |
| [4] | Chen Jian, Tian Jie, Lee N, et al. A partial intensity invariant feature descriptor for multimodal retinal image registration[J].IEEE Transactions on Biomedical Engineering, 2010, 57(7): 1707–1718. doi: 10.1109/TBME.2010.2042169 |
| [5] | Xia Minghui, Bede L. Image registration by "super-curve"[J].IEEE Trans Image Process, 2004, 13(5): 720–732. doi: 10.1109/TIP.2003.822611 |
| [6] | Yang Gehua, Stewart C V, Sofka M, et al. Registration of challenging image pairs: initialization, estimation, and decision[J].IEEE Trans Pattern Anal Mach Intell, 2007, 29(11): 1973–1989. doi: 10.1109/TPAMI.2007.1116 |