2012年以来，笔者在提出弥散化固体电子态系理论的基础上，进一步提出了弥聚子的概念和有关弥聚子运动规律的“弥聚子论”^[1-7].正像量子力学中的“量子”是对表现出显著波动性、但仍葆有粒子性的所有微观粒子的抽象称谓一样，所谓“弥聚子”是笔者对所有实物体的抽象称谓.至于作为经典力学研究对象的客观物体，因其在凸显自身实物“粒子”属性的同时仍蕴涵着内禀的波动性，故可赋予它们一个与“量子”相对的抽象称谓——“隐波子(wave-hidum)”.弥聚子是普适于从微观到宏观的全宇观范围内的一个概念，而量子和隐波子则分别为弥聚子在微观极限和宏观极限情况下的特例.

目前的弥聚子论通过建立全宇观波动方程(对应于薛定谔波动方程)和全宇观质心运动方程(对应于牛顿运动方程)，通过提出全宇观波粒二象性关系(德布罗意波粒二象性关系)和全宇观不确定性关系(海森堡不确定性关系)、包括指出弥聚子的能量蕴含于其波动之中，拓展并部分修正了经典力学和量子力学的基本理论^[3-7]；通过提出低速相对论和全速域相对论拓展并部分修正了狭义相对论^[3-5]；基于“对称性”思辩预言了姗子这种特殊物质的存在以及姗子与电子碰撞产生“自发发射”的机理^[5].其中，笔者提出的全宇观波粒二象性关系的表达式为^[6-7]

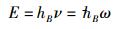
(1a)

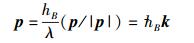
(1b)

其中：E为实物体的能量，ν和ω分别为相应的频率和圆频率，p为实物体的动量，p/|p|为该动量方向上的单位矢量，λ为相应的波长，k为相应的波矢，h_B为全宇观量子化变量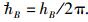，从形式上看，式(1a)和式(1b)这一对表达式与量子力学中的德布罗意波粒二象性关系式几乎是一样的，但实质上，二者之间存在着一个极其重要的差别，德布罗意波粒二象性关系式中的普朗克常数h在这里变成了全宇观量子化变量h_B.

采用唯象方法得出的h_B的具体表达式为^[6-7]

(2)

其中：h为普朗克常数；C_h为比例常数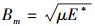； (E^*为全宇观波动方程的定态波函数解中能态分布峰值处的能量，μ为全宇观狭义相对论质量)为弥聚宗量，其变化范围为(0, ∞)；h_Δ为B_m→∞时h_B的取值.显然，h_B的变化范围是从微观极限(B_m=0) 时的h到宏观极限(B_m=∞)时的h_Δ.

弥聚宗量B_m是支配弥聚子从量子变化到确子、支配能态分布从极端聚敛(能级)变化到极端弥散(连续能态)、支配波函数的空间分布从极端弥散(无限漫延)变化到极端聚敛(确定性轨迹)的自变量，是在推导全宇观波动方程过程中自然得出的.

μ的表达式为^[3]

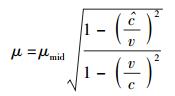
(3)

其中：v为实物体运动的速度，c为实物体的上限速度——光速，为实物体的下限速度——姗速(姗子的速度)，为全宇观相对论的中值基准速度，μ_mid为实物体以中值基准速度运动时的质量，可称作基准质量.

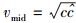
全宇观量子化变量h_B的提出打破了波粒二象性一成不变的定式，使得波粒二象性成为随弥聚宗量B_m的变化而变化的一种“动态”性质，给出了弥聚子从波动性占主导地位的“微观粒子”到粒子性占主导地位的“宏观物体”的演化图像.

关于h_B的具体演化规律，笔者曾认为h_Δ>h，这涉及到了如何正确表征全宇观波动性与粒子性的问题.近来，笔者对这一问题有了新的认识，上述结论随即颠倒了过来，即变成了h_Δ < h.这一变化自然波及到了全宇观不确定性关系，导致了该关系的重要修正，同时还使笔者悟出了光子与姗子之间转化的可能性，进而给出了自发发射、受激吸收和受激发射3个涉及光子与电子相互作用的物理过程的新诠释，预言了相关的第4个物理过程的存在，得出了包含这4个物理过程的、拓展了的爱因斯坦关系以及其他若干新奇的推论和猜想.这些内容将在下面逐一阐述.

笔者曾认为在实物体所具有的能量不变的情况下“频率高意味着波动性强”，根据式(1a)，这意味着在弥聚宗量从0变至无穷大时h_B的值应该逐渐变大，故有h_Δ>h.但当笔者将弥聚子的波动性和光子的波动性联系起来思考时，却发现这一认识是有问题的.光波是一种理想的波动，其波动性已达到无以复加的程度，然而其频率却可高可低，甚至是可以极高、也可以极低.换言之，它所具有的“最强波动性”的性质并不因频率而异！因此，将波动性强弱归结为频率高低应该是错误的.

笔者的最新见解是：波动性的自然强度应该以单位频率中所蕴含的能量、即能量与频率之比(可简称“能频比”)E/ν来表征.而由式(1a)可知，这恰好就是h_B，即

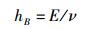
(4a)

因此，h_B就是波动性自然强度的表征.于是，微观情况下的h和宏观情况下的h_Δ便分别应为h_B的最大值和最小值，故有h_Δ < h.

反过来，粒子性的自然强度则应以单位能量所对应的频率、即ν/E来表征.该量恰好是h_B的倒数，即

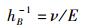
(4b)

当然，依据式(1b)，波动性自然强度和粒子性自然强度的内涵还可以用动量p和波数λ^-1之间的关系来诠释，即波动性自然强度可用单位波数中蕴含的动量来表征，而粒子性自然强度则可用单位动量所对应的波数来表征，具体表达式为

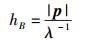
(5a)

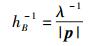
(5b)

为了从数学上更优美地描述弥聚子的波动性和粒子性，可以对波动性和粒子性的自然强度进行一种特殊的归一化，从而定义出值域为(-1，1) 的“双极归一化”波动性强度W_B和“双极归一化”粒子性强度P_B.二者的表达式如下：

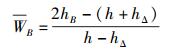
(6a)

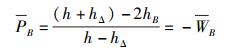
(6b)

借助于上述波动性/粒子性强度的概念，还可以定义归一化弥聚宗量，即

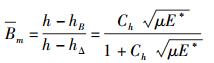
(7)

式(7) 和原先定义的弥聚宗量B_m异曲同工，其区别仅在于前者的变化范围为(0, ∞)，而后者的变化范围为(0, 1).

通过上述讨论，弥聚子波动性及粒子性与弥聚宗量之间的关系已经得到了明晰的诠释.那么，它们与弥聚子所处状态的宏观/微观程度之间又具有怎样的关系呢？实际上，弥聚子的波动性及粒子性完全是由弥聚宗量所决定的，而弥聚子所处状态的宏观/微观程度则既与弥聚宗量相关，又与其运动所受到的空间尺度限制有关.当限制弥聚子运动的空间尺度足够大时，即使其波动性已变得比较强(粒子性比较弱)，亦即其波函数的空间弥漫尺度已经比较大，其所处状态的宏观程度仍然可以是很高的(其微观程度很弱)；反之，当限制弥聚子运动的空间尺度足够小时，即使其粒子性已变得比较强(波动性比较弱)，亦即其波函数的空间弥漫尺度已经比较小，其所处状态的微观程度仍然可以是很高的(其宏观程度很弱).因此，弥聚子所处状态的宏观程度应该是由限制其运动的空间尺度L与其波函数的空间弥漫尺度S的比值L/S来表征，笔者将这一比值叫做宇观度.相应地，弥聚子所处状态的微观程度则应该倒过来由S/L来表征.其中，弥聚子波函数的空间弥漫尺度S是由弥聚宗量所决定的.

以往人们在拓展量子力学适用范围方面所做的努力大多是循着普朗克常数h在宏观领域可以被忽略(h→0) 的思路进行的；而h之所以能够被忽略则被认为是由于它和宏观领域中的许多物理量相比显得微不足道.实际上这是一种很牵强的思路和说法，因为宏观领域中的许多物理量都是可以任意取值的，其值既可以微不足道，也可以巨大无比.问题的真正关键在于在离开微观领域时普朗克常数h已经变得没有意义，而必须用相应的变量来代替.这正是笔者刚刚所介绍的工作.

笔者原来给出的全宇观不确定性关系的表达式为^[6-7]

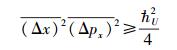
(8)

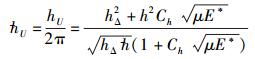
(9)

其中：Δx和Δp_x分别为弥聚子在某一指定方向上位置坐标的不确定性范围和动量分量的不确定性范围，h_U则为当时提出的一个假想变量——全宇观不确定性变量.

基于第1节对全宇观波粒二象性关系给出的新的诠释，有关全宇观不确定性变量h_U的假想已毫无意义，全宇观不确定性关系的表达式自然应修正为

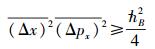
(10)

由此可以得出一个重要的结论：即使是达到了宏观极限，或者说即使当粒子性达到了其上限值，弥聚子的行为仍然存在着由h_Δ所决定的微小的不确定性，而不是变为0.不过，由于事实上此时的不确定性的确已经非常小，所以应有h_Δ≪h.

自发发射、受激发射和受激吸收是光子与物质相互作用(或者更具体地说是光子与电子相互作用)的3个相互关联的物理过程(这里所说的“发射”和“吸收”指的是光子的发射和吸收). 1916年爱因斯坦预言了受激发射的存在，并给出了反映上述3个物理过程相互之间关联性的爱因斯坦关系，确立了光子与物质相互作用的理论基石，导致了20世纪50、60年代脉泽和激光的问世.半个多世纪以来，人们在激光科学与技术领域所取得的巨大成就在很大程度上印证了爱因斯坦理论的正确性.但是，今天看来，这种印证也许是不充分的.笔者提出的姗子概念及所做的“姗子与电子的碰撞是自发发射的成因”的预言，实际上对上述理论构成了挑战.由于姗子这一新的作用要素的介入，有关光子与物质相互作用过程的物理图像和理论描述必然会发生相应的变化.譬如，自发发射既然是由姗子与电子相互碰撞所产生的，这种发射就不是自发的，因而按照“自发”机制去理解和描述该过程便是不合理的.

此外，即使不涉及姗子概念，现有理论本身也存在一些值得质疑之处.譬如：

1) 根据现有理论，处于高能态的电子数和处于低能态的电子数在热平衡的情况下是由费米-狄拉克分布函数稳定地维系着的，于是在热平衡的情况下电子从高能态“自发”地跃迁至低能态缺乏逻辑依据.这正如在具备“失重”条件的舱体中重物是不会“自发”地落向更接近地球表面的舱体底部一样.

2) 在现有理论所包含的上述3个物理过程中，有2个属于发射过程，而只有1个属于吸收过程，其对称美似有所缺失.

3) 光兼以光子和电磁波2种形态存在并运动着，是一种携带着能量的物质.然而，按照现有理论，在光子吸收过程中，光子或相应的电磁波在将自身能量给出之后便彻底消失了，这似乎表明光子除了能量属性之外没有任何其他属性，甚至光子明明具有的动量也“不翼而飞”地突然“失踪”了；而在光子发射过程中，一份释放中的能量会突然间转化为光子，转化为电场和磁场，光子突然无中生有地具有了动量，这无疑又给能量、动量和光子平添了一层神秘的色彩.因此，现有理论包含着哲学上的困惑.

综上所述，现有的光与物质相互作用理论很可能需要修正.

笔者的研究工作表明，基于姗子概念和全宇观波粒二象性理论，可以构建出一个全新的光子、姗子与电子相互作用的物理图像，从而使上述诸多问题迎刃而解.其要点如下：

光子以弥聚子(包括电子，下同)的上限速度(光速c)运动，以电磁波的形式呈现其波动性，并以普朗克常数(全宇观量子化变量的最大值)h作为其波动性的表征；姗子则以弥聚子的下限速度运动，依据姗子与光子之间的对称性推断，姗子也应以类似电磁波的形式呈现其波动性，并以全宇观量子化变量h_B的最小值h_Δ作为其波动性的表征.这样一来，具有同一频率的光子和姗子所具有的能量分别为

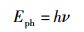
(11)

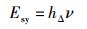
(12)

由于h_Δ≪h，故有

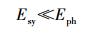
(13)

相应的能量差为

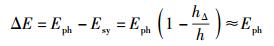
(14)

假定ΔE和E_ph之间的差别小到采用常规的实验仪器难以分辨的程度，则目前公认的对于相关实验结果的理论诠释是否正确就需要重新考证了.譬如，现有理论诠释称“发射或吸收了一个能量为E_ph的光子”，也许真正发射或吸收的能量并不是E_ph，而是较E_ph略小的ΔE.若果真如此，则意味着姗子和光子具有相互转化的可能.具体地，当一个能量为E_ph的光子给出其绝大部分能量ΔE时，它所剩余的能量恰为同频率的姗子的能量E_sy，这意味着它在“被吸收”的过程中可能会转化为同频率姗子；而当一个能量为E_ph的光子是由一个释放出能量ΔE的过程产生时，该光子很可能是由具有同频率姗子能量E_sy的某个物质转化而来的，这个物质自然最有可能就是姗子，或者说该光子的“被发射”过程极有可能是姗子得到能量ΔE而转化为同频率光子的过程.同时，在这一转化过程中，光子和姗子互以对方为动量的遗赠者或继承者，因而其动量得以守恒.这种诠释显然不再与光子的物质属性相悖，因而化解了前面提到的那种哲学层面的困惑.笔者期待着今后会有相关的实验对上述ΔE的存在性加以验证.此外，由上述动量守恒关系还可以得出一个重要的推论.该关系的数学表达式为

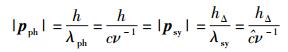
(15)

其中，p_ph和p_sy分别为光子和姗子的动量，而λ_ph和λ_sy分别为光子和姗子的波长.

由式(15) 立得：

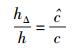
(16)

也就是说，全宇观量子化变量的下限值和上限值之比恰好等于姗速和光速之比.这使得我们对于全宇观量子化变量的下限值h_Δ的认识从定性阶段发展到了定量阶段.

在与电子相互作用时，光子和姗子各有特点.光子恒以弥聚子的上限速度运动，因此它和电子发生相互作用时必是使电子加速，或者说是使电子向较高能级或能谱中的较高能量位置跃迁，相应地光子给予电子能量并随即转化为姗子.姗子则恒以弥聚子的下限速度运动，因此它和电子发生相互作用时必是使电子减速，或者说是使电子向较低能级或能谱中的较低能量位置跃迁，相应地姗子得到电子释放的能量并随即转化为光子.在这些过程中，同频率的光子和姗子之间可能发生某种程度的耦合，进而造成较为复杂的作用机制.

依据上述见解，特别是在统一考虑姗子作用的前提下，可以将现有理论中包含的所谓的“自发发射”以及受激发射和受激吸收3种物理过程重新诠释并重新命名如下.

1) “自发发射”(建议改称“姗激发射”或“姗激光子发射”).频率适当的姗子与某一电子态系中的电子碰撞，使电子的能量降低，其自身则在得到电子释放的能量后转化为光子.在这一过程中起激发作用的只有姗子.

2) 受激发射(建议改称“共激发射”或“共激光子发射”).频率适当的既有光子与同频率的姗子相耦合，促使该姗子与某一电子态系中的电子碰撞，使电子的能量降低，该姗子则在得到电子释放的能量后转化为一个与既有光子同频、同相、同方向、同偏振的新光子.这一过程的特点是光诱姗子激发，既有光子和姗子共同起激发作用，是谓“共激”.

下面将要重新诠释“受激吸收”过程.在此之前，需要做一点特别的说明.该过程的新诠释将不是唯一的，更具体地说，实际上可以对之做2种不同的诠释.所以，在考虑姗子介入的情况下，该过程便自然地派生出2种不同的过程，不妨分别称作“受激吸收A”和“受激吸收B”.下面，即对它们进行具体诠释和命名.

3) 受激吸收A(建议改称“光激吸收”或“光激光子吸收”).频率适当的光子与某一电子态系中的电子碰撞，使电子的能量升高，其自身则在向电子移交能量后转化为姗子.在这一过程中起激发作用的只有光子.显然，它是姗激发射的逆过程.

4) 受激吸收B(建议改称“共激吸收”或“共激光子吸收”).频率适当的既有姗子与同频率的光子相耦合，促使该光子与某一电子态系中的电子碰撞，使电子的能量升高，该光子则在向电子移交能量后转化为一个与既有姗子同频、同相、同方向、同偏振的新姗子.显然，这是一个“共激”过程，而且恰好是“共激发射”的逆过程.

综上所述，由受激吸收过程“一分为二”地派生出来的受激吸收A(光激吸收)和受激吸收B(共激吸收)2种过程分别是姗激发射和共激发射的逆过程.这么一来，原来的3种过程便扩展成了4种过程，而且两两互逆、完美对称，极好地弥补了原有理论的美感缺失.

在下文中，上述4个过程将统一采用新的名称，即“姗激发射”、“共激发射”、“光激吸收”和“共激吸收”.

当然，就实质而言，这些过程无一例外地涉及光子与姗子之间的转化.因此，若分别把它们叫做“姗激姗子-光子转化”、“共激姗子-光子转化”、“光激光子-姗子转化”和“共激光子-姗子转化”自然也是可以的，而且从逻辑上更明晰.不过考虑到长期以来人们所形成的习惯，还是采用刚才约定的叫法为好.

如前所述，现有理论中关于光子与电子相互作用3个物理过程之间的关系是由爱因斯坦给出的，亦即著名的爱因斯坦关系.相应地，这里将给出光子、姗子与电子相互作用4个物理过程之间的关系.

设在某一电子态系中存在E₁、E₂ 2个能级(或能量位置，下同).电子占据这2个能级的几率由费米-狄拉克分布来描述.在热平衡状态下，这2个几率的表达式分别为

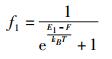
(17)

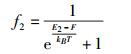
(18)

其中：F为该电子态系中的费米能级，k_B为波尔兹曼常数，T为温度.

设任意情况下和热平衡时的光子能量分谱密度分别为P_ph(E_ph)和P′_ph(E_ph).后者的表达式为

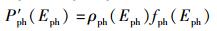
(19)

其中：ρ_ph(E_ph)为光子态密度；f_ph(E_ph)为热平衡时光子占据态的几率，由玻色-爱因斯坦分布给出，即

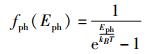
(20)

类似地，设任意情况下和热平衡时的姗子能量分谱密度分别为P_sy(E_sy)和P′_sy(E_sy).后者的表达式为

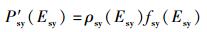
(21)

其中：ρ_sy(E_sy)为姗子态密度，f_sy(E_sy)为热平衡时姗子占据态的几率.鉴于姗子与光子之间所应具有的对称关系，笔者认为该几率也由玻色-爱因斯坦分布给出，即

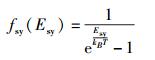
(22)

为了比较方便，在推导光子、姗子与电子相互作用4个物理过程之间的关系之前，有必要先介绍爱因斯坦当年在未考虑姗子介入的情况下所给出的自发发射、受激发射和受激吸收3个物理过程中电子跃迁速率的唯象表达式以及藉之得出的爱因斯坦关系^[8].

该组跃迁速率唯象表达式为

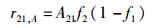
(23)

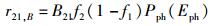
(24)

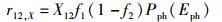
(25)

其中A₂₁、B₂₁和X₁₂为相应的跃迁系数，按照爱因斯坦的预想，它们均应为由材料本身决定的常数，而与温度无关.

鉴于爱因斯坦理论中并没有考虑姗子介入的情形，笔者仅从上述唯象表达式中无法确定这里的受激吸收在考虑姗子介入的情况下所对应的到底是“受激吸收A”，还是“受激吸收B”，故在式(25) 表示受激吸收电子跃迁速率和跃迁系数的记号中出现了字母X，而没有采用字母A或B.

由热平衡时上述3个速率所应满足的条件：

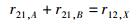
(26)

即可导出著名的爱因斯坦关系，即

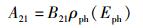
(27)

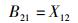
(28)

应该指出，这一关系是在爱因斯坦将受激发射引入光与物质相互作用的范畴之后才得出的.若在上述推演中去掉受激发射过程，即令r_{21, A}=r_{12, X}，立即会有

(29)

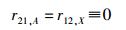
(30)

这表明，不考虑受激发射的理论模型是不符合客观世界的基本逻辑的.

现在转而考虑姗子介入的情况.姗激发射、共激发射、光激吸收和共激吸收4个物理过程中电子跃迁速率的唯象表达式可以依次写为

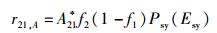
(31)

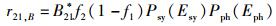
(32)

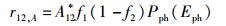
(33)

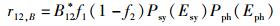
(34)

其中A₂₁^*、B₂₁^*、A₁₂^*和B₁₂^*为相应的跃迁系数.沿袭爱因斯坦的唯象思路，笔者设定它们均为由材料本身决定的常数，而与温度无关.

热平衡时上述4个速率所应满足的条件为

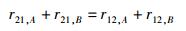
(35)

解之立得以下一组关系：

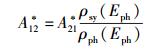
(36)

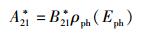
(37)

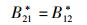
(38)

这一组关系的得出表明，诸跃迁系数可以有非零解，故考虑姗子介入的理论模型是符合客观世界的基本逻辑的.

如果舍弃光激吸收和共激吸收2个物理过程中的任意1个，即令r_{12, A}=0或r_{12, B}=0，热平衡时诸过程跃迁速率所应满足的条件即变为

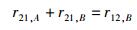
(39)

或

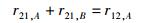
(40)

求解式(39) 可以得出以下一对关系：

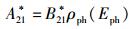
(41)

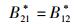
(42)

求解式(40) 则只能得到所有系数和所有速率的零解，即

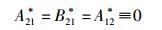
(43)

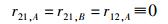
(44)

这表明，仅包含姗激发射、共激发射和光激吸收3个过程的理论模型是不符合客观世界的基本逻辑的.因此，在爱因斯坦将受激发射引入了光与物质相互作用的范畴时，尽管由于并不知晓姗子的存在而没有指明该过程到底是对应于受激吸收A(光激吸收)，还是对应于受激吸收B(共激吸收)，但是他引入的实际上只能是受激吸收B(共激吸收).

据此，笔者有理由在爱因斯坦理论中的受激吸收速率表达式(24) 里将记号X替换为记号B，于是式(25) 变为

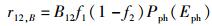
(45)

进而，可将爱因斯坦关系中的第2个式子，即式(28) 重写为B₂₁=B₁₂.为体现爱因斯坦关系的完整性及阅读方便，兹将式(27) 原式和式(28) 重写后的形式一并列出：

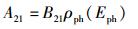
(46)

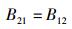
(47)

下面，进一步探讨考虑姗子介入的4过程理论(以下简称“4过程理论”)和爱因斯坦3过程理论(以下简称“3过程理论”)之间的联系与差别.为方便对比，将前面已经给出的4过程理论中的跃迁速率表达式，即式(31)~(34) 略做变形如下：

(48)

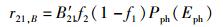
(49)

(50)

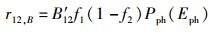
(51)

其中：

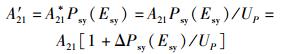
(52)

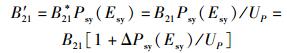
(53)

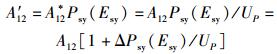
(54)

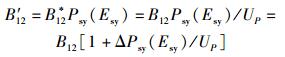
(55)

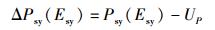
(56)

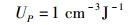
(57)

由前述已知，4过程理论中的式(48)、式(49)、式(51) 是和3过程理论中的式(23)、式(24)、式(45) 相对应的.每对表达式除了所有跃迁系数均差一个因子P_sy(E_sy)/U_P外，形式上是完全一致的.由于因子P_sy(E_sy)/U_P是与温度相关的，所以4过程理论中相应的3个跃迁系数A′₂₁、B′₂₁和B′₁₂都是与温度相关的，或者说都不是仅由材料本身决定的常数.故从严格意义上讲，若4过程理论是正确的，3过程理论中将跃迁系数A₂₁、B₂₁和B₁₂设定为常数就是不正确的，进而3过程理论必须由4过程理论取代.此点之真伪尚待特殊设计的相关实验得出结论.

同时，借助于式(48)~(57) 所给出的关系，4过程理论中由式(36)~(38) 所给出的4个跃迁系数之间的关系立即变为

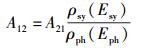
(58)

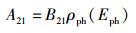
(59)

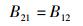
(60)

显然，式(59) 和式(60) 与3过程理论中的爱因斯坦关系即式(46) 和式(47) 完全相同，呈现出一种自然契合之美.至于式(58)，由于它是和4过程理论所独有的光激吸收过程相联系的，所以在爱因斯坦关系中没有对应的表达式，实不足为奇.

3过程理论、特别是其中的爱因斯坦关系在实际应用中获得了巨大的成功.因此站在4过程理论的立场上来看，它所疏漏的光激吸收过程应该较之其他3个过程弱得多.

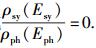
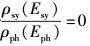
极而言之，只要令A₁₂=0，光激吸收过程便在4过程理论中消失.而由式(58) 可知，A₁₂=0等价于A₂₁ = 0或不过，很容易看出，A₂₁=0显然是不可能的，因为它将导致B₂₁=B₁₂=0同时发生，而这将意味着光与物质的相互作用不复存在.因此，光激吸收过程消失的条件便只能是，而显然这又等价于ρ_sy(E_sy)=0，其物理意义为姗子态的消失.可是，若姗子态真的消失了，必有姗子能量分谱密度P_sy(E_sy)=0.由式(48)~(57) 可知，这将导致4过程中其余3个过程与受激吸收过程“同归于尽”，而这同样意味着光与物质的相互作用不复存在.可见，严格地讲，光激吸收过程不管多么弱，却总是存在的，不可能彻底消失.

于是，真正需要探讨的是在什么条件下A₁₂→0.显然，这个条件应该是

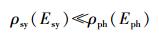
(61)

也就是说，姗子态密度远小于光子态密度——这是一个非常重要的推论.也许，这正是姗子一直没有被人们发现的原因.

在A₁₂→0的前提下，可以近似地认为光激吸收过程消失了.这样一来，4过程理论就又变成了3过程理论，不过它还不是爱因斯坦原来提出的3过程理论，故笔者称之为“准3过程理论”.该理论的跃迁速率表达式自然就是前面给出的式(48)、式(49) 和式(51).从这3个表达式以及相关的式(52)、式(53)、式(55) 以及式(56) 和式(57) 出发，可以进一步来探究准3过程理论和3过程理论之间的关系.

令P_sy(E_sy)/U_P=1，式(48)、式(49) 和式(51) 即变为3过程理论的式(23)、式(24) 和式(45).由此可见，仅当姗子能量分谱密度P_sy(E_sy)在指定姗子能量E_sy处的值恰好为单位能量分谱密度值时，准3过程理论的诸表达式才全同于3过程理论中的相应表达式.因此，对于姗子能量分谱密度取任意值时的情形，3过程理论充其量只是准3过程理论乃至4过程理论的一种近似.

笔者认为，4过程理论更为全面、深刻地揭示了光子、姗子与电子相互作用的规律，因而更具普遍意义和科学价值.依据4过程理论，笔者目前已经能够预言姗子激射的可能性及姗子激射的条件(类似于现有理论所给出的孤立能级系统中的粒子数反转条件和半导体电子态系中的杜拉福格条件)；而一旦姗子的发射成为一个可操控的过程，则通过将光子转化为姗子、必要时再使之恢复为光子便可以实现“超级慢光”，从而从根本上解决光通信中的光缓存问题.此外，既然姗子已经成为合理且完备地诠释上述4个过程、特别是其中2个发射过程(姗激发射和共激发射)的要素，现行量子场论中有关“真空起伏”引发“自发发射”(姗激发射)的观点^[9]似乎就可以被扬弃了.但是，这并不意味着量子场的“真空起伏”在整个弥聚子论中可以不予考虑.恰恰相反，鉴于量子场“真空起伏”具有几率特征，且弥聚子几率波行为的强弱程度又由全宇观量子化变量决定(弥聚子在宏观情况下的几率波行为远小于在微观情况下的几率波行为)，一个合理的、非常重要的猜想便产生了：量子场的“真空起伏”应该能够作用于弥聚子而使之产生几率波行为，因而在全宇观量子化变量中必定已包含了量子场“真空起伏”的信息.该信息可能表现为一个因子，在正常情况下该因子可能恰好为常数1.而若量子场的“真空起伏”不总是处于正常情况下的恒定水平，则该因子就可能在(0，1) 或(1，∞)的范围内变化.当量子场完全消失时，该因子为0，从而使得全宇观量子化变量为0，此时的弥聚子将仅具有粒子性而不具有波动性；相反，当量子场达到无穷大时，该因子也将变为无穷大，此时的弥聚子将仅具有波动性而不具有粒子性.不过，这只是一个“思想实验”.在现实的物理世界中，量子场的“真空起伏”应该总是处于正常情况下的恒定水平，因此该因子恒为常数1，全宇观量子化变量将只是在h和h_Δ之间变化，弥聚子将始终兼具粒子性和波动性.

综上所述，量子场的真空起伏可能是弥聚子几率波行为产生的根源.若果真如此，则爱因斯坦关于“上帝不会掷骰子”的断语就应该是对的.因为按照这一认识，弥聚子的几率波行为并不是与生俱来的，也就是说上帝的确没有以“掷骰子”的方式来规范它的行为；实际上“掷骰子”的是量子场的“真空起伏”！希望这一猜想能够在今后的研究工作中得到证实.

在弥聚子波动性与粒子性表征问题上所得出的新结论使得笔者先前提出的全宇观波粒二象性关系和全宇观不确定性原理得以完善，从而使得整个弥聚子论建立在了更为牢固的基础之上.光子与姗子相互转化的新见解、“光激吸收”与“共激吸收”并存的预言、姗子态密度远小于光子态密度的推论以及对于爱因斯坦关系的拓展更深刻地揭示了相关物理过程的本质，深化了对于姗子特性的了解，构成了光子、姗子与物质相互作用新理论的基础.笔者还推测了姗子激射和实现“超级慢光”的可能性，提供了更合理地诠释几率波成因的线索，并就采用实验方法验证上述这些理论正确性的切入点提出了建议.