提出了基于指数嵌入族(EEF)准则的认知无线电宽带频谱感知算法.在EEF准则宽带感知算法的基础上, 充分考虑信号子空间和噪声子空间的性质, 利用Gerschgorin酉变换改进EEF算法, 提出了基于Gerschgorin EEF(GEEF)的宽带感知算法.该方案主要是利用EEF准则或GEEF准则估算出授权频带中被主用户占用子带集合的势, 从而完成宽带授权频段上空闲频带的感知, 以便于被次级用户动态接入.理论推导和仿真结果表明, 所提出的方案无须知晓任何有关噪声功率和主用户信号的先验信息, 对噪声功率的不确定性具有鲁棒性.
Exponentially embedded families (EEF) criterion based wideband spectrum sensing schemes were proposed for cognitive radios. Based on the EEF criterion, the signal and noise subspaces were considered in spectrum observation data and the EEF wideband sensing was improved by employing Gerschgorin unitary transformation in data processing. Correspondingly, the developed wideband sensing algorithm was operated under Gerschgorin EEF (GEEF) criterion. The proposed two algorithms estimate the cardinality of the primary user signal occupied subband set via EEF or GEEF criterion to identify idle subbands for secondary users dynamically accessing the licensed frequency band. Analysis and simulation verify that the proposed algorithms do not need any a prior knowledge of the noise power and the primary user signal. They are robust against the noise power uncertainty problem.
认知无线电[1-2]作为一种新颖的技术,通过机会频谱接入,能有效地解决当前频谱利用率低下的问题.次级用户(SU, second users)动态接入空闲的主用户(PU, primary user)授权频带时,必须对PU不产生干扰,因而需要SU准确地感知授权频带的忙闲状态.由此,频谱感知技术成为认知无线电的一项关键技术.传统的频谱感知技术研究主要集中在窄带频谱感知以及多用户合作感知上.近年来,宽带频谱感知开始受到了广泛的关注,出现了一些相关文献[3-4].然而,这些研究或多或少存在自身的不足,主要表现为对PU信号先验信息的依赖.能量检测(ED, energy detection)[5]因其不需要关于PU信号的任何先验信息的优点受到广泛的研究.然而,实际应用中,由于受到噪声功率不确定性的影响,ED的性能受到极大影响.
针对以上研究的不足,笔者提出了2种宽带频谱感知算法:基于EEF准则和基于GEEF准则的宽带频谱感知算法.这2种算法都基于接收信号的协方差矩阵特征值和特征向量信息,通过EEF准则或GEEF准则估计出授权频带中被PU占用子带集合的势(COSS, cardinality of occupied subband set),从而完成对整个授权中各个子带状态的鉴别.结合EEF准则和Gerschgorin定理提出的GEEF宽带感知算法,通过Gerschgorin酉变换[6]充分利用信号与噪声子空间之间的特性,明显提升了算法的性能.
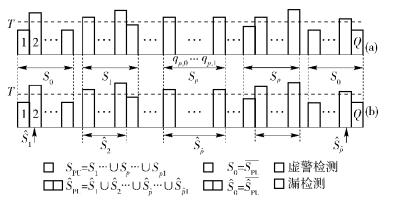
1 宽带系统模型考虑授权频带带宽为W Hz,整个宽带授权频谱被认知无线电系统等分为Q个互不重叠的带宽为W/Q Hz的子带.如图 1(a)所示,考虑P个PU独立工作在授权频带不同的子带上,其中第p个PU占用子带集合为Sp={qp, 0, qp, 0+1, …, qp, 1-1, qp, 1}, qp, 0、qp, 1分别表示第p个PU占用子带的起始位置和终止位置;PU占用子带集合为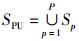
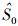
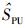
|
图 1 宽带感知模型 |
在二元假设模型下,采用Hq, 1表示第q个子带处于被占用状态,Hq, 0表示第q个子带处于空闲状态,则第n次快拍时第q个子带上采样信号为
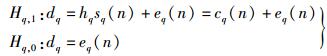
|
(1) |
其中:hq为第k个子带上的信道增益,sq(n)为第n时刻PU发送的信号,eq(n)为第n时刻第q个子频带上接收到的噪声.
第n次快拍时Q个子带采样信号联合表示为
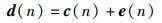
|
(2) |
其中:d(n)=[d1(n), d2(n), …, dQ(n)]T; c(n)=[c1(n), c2(n), …, cQ(n)]T为均值为0,协方差矩阵为E[c(n)cH(n)]的独立同分布循环对称复高斯随机向量;e(n)=[e1(n), e2(n), …, eQ(n)]T为独立同分布循环对称复高斯的加性噪声向量.
2 COSS算法理论分析接收端采样数据的协方差矩阵为
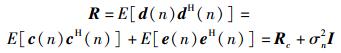
|
(3) |
其中:Rc为接收端PU信号协方差矩阵;σn2I为噪声协方差矩阵,σn2为噪声功率,I为单位矩阵.由于信号与噪声间的独立性,R为满秩对角矩阵.
由式(3) 可知,被占子带的功率为PU信号功率与噪声功率之和,而空闲子带的功率仅来自于噪声功率.因此,一般来说,瞬时功率大的子带更有可能被PU占用,应归属于集合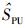
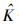
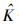
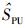
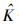
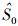
步骤1 计算出每个子带上N次采样的能量值大小θq(q=1, 2, …, Q).
步骤2 将它们按照降序进行排列:
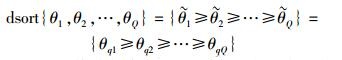
|
步骤3 估计集合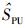
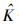
步骤4 根据求得的个数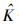
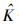
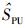
由分析可知,COSS宽带感知算法的关键在于步骤3中集合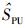
EEF[7]准则的函数表达式为
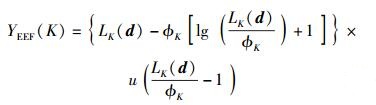
|
(4) |
其中:ϕK为自适应参数的个数;u(·)为单位阶跃函数;LK(d)为似然比,定义为
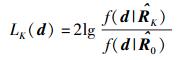
|
(5) |
其中:d=[d(1), d(2), …, d(N)]T为接收的数据向量,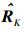
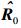
根据矩阵特征分解理论,协方差矩阵R能表示为
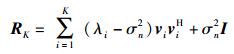
|
(6) |
其中:λ1≥λ2≥…≥λK和v1, v2, …, vK分别为RK的特征值和对应的特征向量.此时的参数向量Θ(K)=[λ1, …, λK, σn2, v1H, …, vKH]T.
将RK的估计值代入式(4),化简可得到
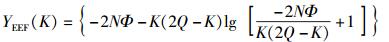
|
(7) |
其中Φ=μ+β+γ,而
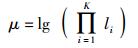
|
(8a) |
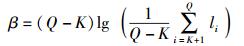
|
(8b) |
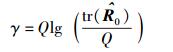
|
(8c) |
其中:l1≥l2≥…≥lK≥lK+1≥…≥lQ为矩阵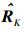
EEF准则所估计出的集合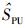
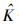
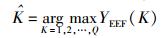
|
(9) |
集合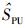
利用R的前(Q-1) 行、前(Q-1) 列组成的子矩阵R1的特征向量构造特殊酉矩阵[6]为
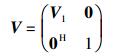
|
(10) |
其中:V1=[v′1, v′2, …, v′Q-1],0为Q-1维全0向量.
利用特殊酉变换矩阵V对协方差矩阵R进行酉变换,可以得到

|
(11) |
其中:λ′1≥λ′2≥…≥λ′K≥λ′K+1=…=λ′Q-1, λ′i(i=1, 2, …, Q-1) 为Gerschgorin圆心,元素ρi=v′iHr(i=1, 2, …, Q-1) 为Gerschgorin圆半径.对于i=K+1, K+2, …, Q-1,由于噪声子空间与信号子空间正交,因而Gerschgorin圆半径ρi=0[6].
将ZK的估计值代入式(5),化简可得似然比函数为
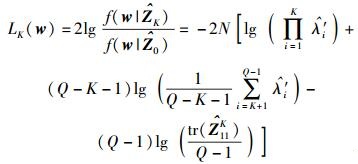
|
(12) |
其中:w=VHd为经酉变换后的接收数据向量,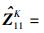

将式(12) 代入式(4),可构造GEEF准则为

|
(13) |
其中ηK为自适应参数的个数.
4.2 基于GEEF的宽带感知同EEF类似,将ZK的估计值代入式(13),化简可得到
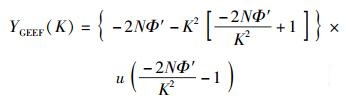
|
(14) |
其中Φ′=μ′+β′+γ′,而
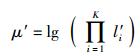
|
(15a) |
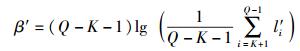
|
(15b) |
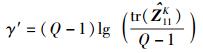
|
(15c) |
其中:l′1>l′2>…>l′K>l′K+1>…>l′Q-1为矩阵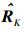
GEEF准则所估计出的集合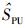
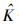
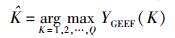
|
(16) |
集合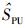
与传统频谱感知算法相比,基于COSS估计的宽带频谱感知算法优势在于:① 无须预知PU信号的先验信息,可实现有效的盲频谱感知;② 避免了对噪声功率进行估计,提升了对抗噪声不确定性的鲁棒性.具体地,与Akaike信息准则(AIC, akaike’s information criterion)、最小描述长度(MDL, minimum description length)[8]准则相比,虽然EEF准则的结构更为复杂,但其不仅克服了AIC不满足一致性的问题,而且克服了MDL低信噪比时检测能力不足的问题.在EEF的基础上,通过Gerschgorin酉变换,GEEF频谱感知算法还充分利用了信号子空间与噪声子空间的特性,使得感知性能得到较大的改善.
5 仿真结果及分析采用Matlab仿真时,设定Q=40,K=12.与ISTT*、AIC、MDL、GAIC、GMDL[9]宽带感知算法进行比较.对于ISTT算法,考虑噪声功率的不确定度α=10lgAdB[10],即估计值在区间[σn2/A, Aσn2]上服从均匀分布.仿真中,对于ISTT检测,固定虚警率Pfa=0.1,考虑α=0 dB和α=1 dB 2种情况.
*ED在宽带感知中采用独立载波阈值检测(ISTT, individual subband threshold test)来实现,即
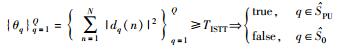
|
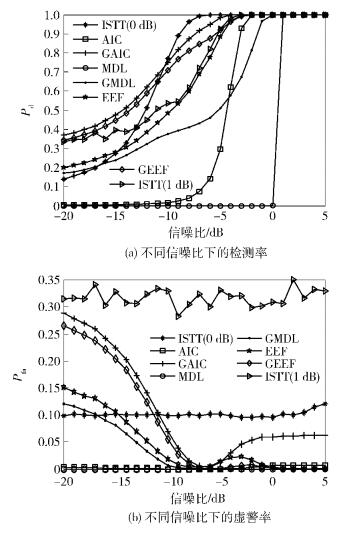
仿真1 图 2所示为N=1 000时各种算法检测率Pd和虚警率Pfa随信噪比变化的性能曲线.由图 2可以看出,ISTT算法的性能在α=0 dB时相对较好,但其性能受噪声不确定性影响较大;AIC、MDL算法的性能在低信噪比时较差;EEF感知算法的性能较AIC、MDL有较大改善;改进后的GAIC、GMDL、GEEF性能都较之原算法性能有较大提升,而且GEEF感知算法在性能与GAIC相仿时满足一致性.
|
图 2 基于Gerschgorin圆盘理论感知算法在不同信噪比下的检测率和虚警率 |
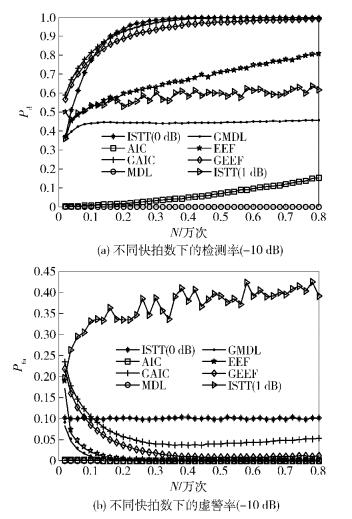
仿真2 图 3所示为信噪比为-10 dB时,各算法性能随快拍数N的变化曲线.由图 3可以看出,性能相对稳定的ISTT(α=0 dB)感知算法受噪声不确定性影响很大, α=1 dB时,Rfa很高,而且当快拍数N超过一定大小时,Pd受信噪比墙影响不再升高[9];受自身检测能力的限制,AIC、MDL、GMDL算法难以满足低信噪比下的要求.就Pd而言,GAIC、GEEF感知算法的性能相仿(与ISTT(α=0 dB)相似),较之EEF感知算法更优,更能满足实际应用要求;就Pfa而言,GAIC、GEEF感知算法的Pfa相比ISTT更低,而且GEEF感知算法低于GAIC感知算法.
|
图 3 基于Gerschgorin圆盘理论感知算法在不同快拍数下的检测率和虚警率 |
基于宽带频谱感知理论,提出了基于EEF准则的宽带频谱感知方案.在此基础之上,结合Gerschgorin定理,提出了改进的GEEF准则宽带感知算法.理论分析和仿真结果表明,所提出的感知方案不仅能解决ED宽带感知算法性能受噪声功率不确定性影响较大的问题,而且不依赖PU信号的先验信息,具有很强的可实现性.
| [1] | Haykin S. Cognitive radio: brain empowered wireless communications[J].IEEE Journal on Selected Areas in Communications, 2005, 23(2): 201–220. doi: 10.1109/JSAC.2004.839380 |
| [2] |
徐任晖, 陈明, 张剑峰, 等. 认知无线电OFDM系统的最优频谱感知周期选择[J]. 北京邮电大学学报, 2011, 34(3): 98–102.
Xu Renhui, Chen Ming, Zhang Jianfeng, et al. Sensing period optimization for OFDM-based cognitive radio[J].Journal of Beijing University of Posts and Telecommunications, 2011, 34(3): 98–102. |
| [3] | Hwang C H, Lai G L, Chen S C. Spectrum sensing in wideband OFDM cognitive radios[J].IEEE Transactions on Signal Processing, 2010, 58(2): 709–719. doi: 10.1109/TSP.2009.2032453 |
| [4] | Doris B, Luca D V, Sergio R. A histogram-based segmentation method for wideband spectrum sensing in cognitive radios[J].IEEE Transactions on Instrumentation and Measurement, 2013, 62(7): 1900–1908. doi: 10.1109/TIM.2013.2251821 |
| [5] | Cabric D, Tkachenko A, Brodersen R W. Experimental study of spectrum sensing based on energy detection and network cooperation[C]//ACM Int. Workshop on Technology and Policy for Accessing Spectrum. 2006: 1289-1297. |
| [6] | Wu Hsien-Tsai, Yang Jar-Ferr, Chen Fwu-Kuen. Source number estimation using transformed Gerschgorin radii[J].IEEE Transactions on Signal Processing, 1995, 43(6): 1325–1333. doi: 10.1109/78.388844 |
| [7] | Kay S. Exponentially embedded families-new approaches to model order estimation[J].IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(1): 333–344. doi: 10.1109/TAES.2005.1413765 |
| [8] | Liu Siyang, Shen Junyang, Zhang Ranran. Information theoretic criterion based spectrum sensing for cognitive radio[J].IET Communications, 2008, 2(6): 753–762. doi: 10.1049/iet-com:20070405 |
| [9] | Qing Haobo, Liu Yuanan, Xie Gang. Robust spectrum sensing for blind multiband detection in cognitive radio systems: a Gerschgorin likelihood approach[J].KSII Transactions on Internet and Information Systems, 2013, 7(5): 1131–1145. doi: 10.3837/tiis.2013.05.011 |
| [10] | Tandra R, Sahai A. SNR walls for signal detection[J].IEEE Journal of Selected Topics in Signal Processing, 2008, 2(1): 4–17. doi: 10.1109/JSTSP.2007.914879 |


