2. 桂林电子科技大学 信息与通信学院, 广西 桂林 541004
提出一种增强型无线传感器网络的小道消息(gossip)时间同步算法, 利用无线信道的广播特性来提高同步性能.传统的gossip同步算法是点对点的通信方式, 增强型gossip同步算法是点对多点的通信方式.理论分析和计算机仿真均表明此方法可以提高无线传感器网络时间同步的收敛速度, 并且可以降低网络能耗.
2. Information and Communication College, Guilin University of Electronic Technology, Guangxi Guilin 541004, China
An enhanced gossip time synchronization algorithm for wireless sensor networks was proposed to improve the performance of synchronization by integrating the broadcasting characteristics of wireless channel. The communication mode of traditional gossip algorithm is peer to peer, while the mode of the proposed algorithm is peer-to-multi. Both analysis and simulation confirm the effectiveness of the proposed algorithm in expediting the convergence rate and reducing the energy consumption.
时间同步是无线传感器网络的一项重要关键技术,它对网络的数据融合、位置感知、协同传输、网络安全等有重要意义[1].分布式无线网络对时间同步的要求有3种方式[2]:第1种方式是时间排序,仅需处理事件或消息的先后顺序;第2种方式是相对时间同步,即维护本地网内的相对时钟关系,要求所有节点达到统一的时间尺度;第3种方式是绝对同步,要求所有节点的时钟同步到一个参考时钟.无线传感器网络中,各个感知节点对监测的数据需要做网内处理,如压缩融合、分布式平均等,然后传给中心节点.在这种情况下需要实现网内节点的绝对时间同步.合议一致性算法[3]、gossip算法[4]及广播算法[5]均可以实现网内绝对时间同步.合议一致性同步算法要求每个节点知道自己所有的邻居关系,通信开销相对较大. gossip同步算法通信开销比较小,但是其收敛速度慢,网络能耗高.由于广播同步算法每次只有广播节点的邻居节点能更新时钟信息,广播节点及其他节点不能更新当前的时钟信息,所以收敛速度相对较慢.
针对上述问题,提出一种增强型gossip同步算法,旨在实现无线传感网络的网内时间同步,提高同步收敛速度,降低能耗.增强型gossip同步算法利用无线信道的广播特性,一对节点在进行gossip过程中,其中一个节点在向对方发送时间信息时,处在其广播域的许多节点能接收此信息.这些节点将接收到时间信息和本地时间信息的平均值作为自己的更新时钟.这样的过程在每对邻居节点之间反复进行,最终网络所有节点的时钟信息会收敛到一个相同的值,从而实现了网内时间的绝对同步.
1 网络模型假定研究对象为由N个传感器随机连接组成一个连通的无线传感器网络.用一个连通无向图G=(V, E)来建模此网络,其中顶点集合V={1, 2, …, N}表示网络中的N个传感器节点,边集合E={eij}表示网络节点i和j之间的通信链路.节点i广播域的所有节点所组成的集合称为节点i的邻居节点集合,记为Si={p|eip∈E},集合Si的元素个数|Si|称为节点i的度,记为di=|Si|.节点i和节点j的共同广播域中的所有节点组成的集合称为节点i和节点j公共邻居节点集合,记为Rij={m|eim∈E, ejm∈E}.
2 传统的Gossip同步算法假定在n时刻,节点i和其邻居节点j在进行gossip同步算法.传统gossip算法(TGA,traditional gossip algorithm):节点i把自己当前时刻的时间信息(时钟相位与时钟频率)φi(n)=(ti(n), Ti(n))发送给节点j,节点j接收到此信息后,把自己当前时刻的时间信息φj(n)=(tj(n), Tj(n))发送给节点i,节点i和节点j分别设置自己n+1时刻的时间信息值为收到的时钟信息和本地时钟信息的平均值,其他节点的时间信息保持不变,如式(1) 所示.
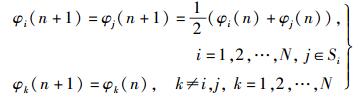
|
(1) |
TGA有以下结论:图G每条边的2个节点进行gossip同步算法,这样的过程反复进行,最终会使各节点的时间信息渐进地收敛于它们初始值的平均值[4].
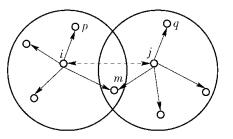
3 增强型的Gossip同步算法3.1 增强型Gossip同步算法TGA中,节点i将自己当前时刻的时钟信息φi(n)发送给其邻居节点j时,由于无线信道的广播特性,处于节点i的广播域中的其他所有节点p∈Si也能收到此信息.同样,节点j将自己当前时刻的时钟信息φj(n)发送给节点i时,处于节点j的广播域中的其他所有节点q∈Sj也能收到此信息,如图 1示.处于广播域的上述节点对收到的时钟信息未作任何利用.
|
图 1 增强型gossip算法示意图 |
基于上述情况,提出一种增强型gossip算法(EGA,enhanced gossip algorithm),发送节点广播域中的各个节点对收到的信息和自己当前的信息平均后作为下一个时刻的时钟更新值.算法描述如下:假定n时刻网络中的2个相邻的节点i、j进行gossip同步算法. ① 节点i把自己当前时刻n的时钟信息φi(n)发送给节点j,节点j和处于节点i的广播域中的其他所有节点p∈Si接收此信息;② 节点j把自己当前时刻n的时钟信息φj(n)发送给节点i,节点i和处于节点j的广播域中的其他所有节点q∈Sj接收此信息;③ 假定所有节点都能正确估计对方所发送的时钟信息,节点i、j分别将自己n+1时刻的时间信息设置为两者的平均值,节点p、q设置n+1时刻的时间信息为自己当前时刻的时钟值和接收到的时钟值两者的平均值,处于节点i、j共同广播域的节点m∈Si∩Sj设置n+1时刻的时钟信息为自己当前时刻的时钟值和接收到节点i、j的时钟值三者的平均值;④ 其他节点时间信息保持不变.上述时钟更新表示为
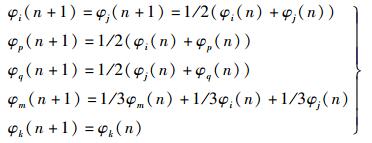
|
(2) |
定义矩阵B(n)=Bij为增强型gossip素矩阵,其中bii=bij=bji=bjj=bpi=bqj=1/2,bkk=1,bmi=bmj=bmm=1/3,k≠i, j, k=1, 2, …, N,p∈Si,q∈Sj,m∈Si∩Sj,其他元素为零.显然B(n)为行随机矩阵.假定图G有K条边,这K条边分别进行一遍EGA后就有K个增强型gossip素矩阵,这些矩阵的乘积定义为增强型gossip矩阵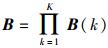
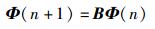
|
(3) |
引理1[5] 设P是不可约随机矩阵,则矩阵P的谱半径ρ(P)=1;对于任一正向量z,有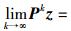
定理1 在一个连通的无线传感器网络中,对其相应模型图G中的每条边依次进行EGA,此过程反复进行,图G中所有节点的时钟信息最终将趋向一致.即
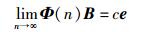
|
(4) |
其中:c为某个常数,e为全1列向量.
证明 在任意时刻n,节点对(i, j)进行EGA过程中,增强型gossip素矩阵B(n)为一个随机矩阵,所以B也为一个随机矩阵.由于图G为连通图,所以矩阵B的伴随有向图D(B)为强连通图.非负矩阵A为不可约矩阵的充分必要条件是矩阵A的伴随矩阵有向图D(A)是强连通的[6].所以矩阵B为不可约随机矩阵.从而有
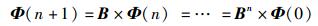
|
(5) |
由引理1有
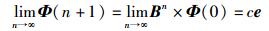
|
(6) |
式(6) 说明通过对无线传感器网络中每个节点对之间依次反复进行EGA,最终会使网络中所有节点的时间频率和相位达到一致,即实现了网络的绝对时间同步.定理1得证.
3.2 与TGA的比较平均时间同步协议(ATSP,average time synchronization protocol)算法是由Wu[4]等最近提出的一种无线传感器网络时间同步协议.此算法是一种TGA.下面对EGA和ATSP同步算法在收敛速度及能耗等方面做定性分析或定量比较.
EGA充分利用无线信道的广播特性来提高同步的收敛速度和降低网络能耗.在EGA中,节点i和节点j在进行时钟更新的同时,它们的邻居节点p∈Si及q∈Sj也在进行时钟更新;而在TGA中,p∈Si及q∈Sj在以后的时隙内才能分别进行时钟更新,所以EGA中的收敛速度要快于TGA. EGA的收敛速度与网络拓扑结构有关,与节点的平均度d=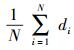
无线传感器网络是能量受限的分布式网络,在设计其算法时必须考虑能耗问题[7].所以高能效通信协议对延长无线传感器网络的生命周期是至关重要的. EGA中节点对之间在进行信息交换时,其邻居节点通过接收时钟信息进行时钟更新,并未增加发射消息的数量.而且由于网络的同步收敛时间减少了,总体的消息发射减小了,所以降低了网络能耗.
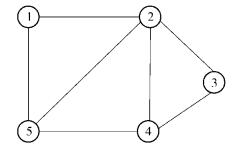
4 仿真结果仿真实验环境为由N=5个感知节点组成连通的分布式无线网络.由于频率同步原理和相位同步相同,这里只对相位同步的相关性能进行仿真验证.建立2种不同的网络拓扑进行比较分析,一种为图 2所示的任意连接的网络;另一种为环形拓扑网络.
|
图 2 随机连通的无线传感器网络 |
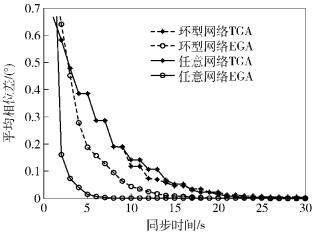
图 3所示为初始相位正态分布的情况下进行的仿真实验.实验中假定一个同步时隙为1 s,相位的单位用度表示.由图 3可以看到EGA的收敛速度都比TGA的收敛速度快.这是因为在同一个同步时隙内,TGA只有2个节点在更新时钟,而EGA就有至少4个节点在更新时钟.快的程度与网络拓扑有关,节点的平均度越大,收敛速度越快.实验结果均符合预期的理论分析.
|
图 3 收敛速度 |
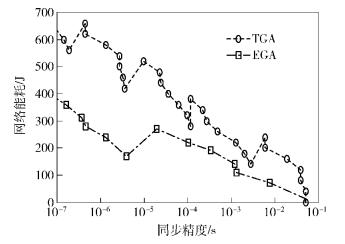
传统的同步算法提高同步精度必须增加发射消息数量. EGA并未增加发射节点的数量,只是增加了同一个同步时隙内的接收节点的数量. EGA的收敛速度提高了,在同一精度的前提下,EGA所需同步时间减少了,消息交换也减少了,所以网络能耗降低了.在仿真中,假定传感器节点发送和接收一个同步消息消耗能量均为10 J. 图 4所示为EGA和TGA中同步精度与能耗的仿真比较.从图 4中可以看到,要达到相同的同步精度,EGA的能耗比TGA的能耗低,此结果符合预期理论分析.
|
图 4 网络能耗性能 |
提出一种EGA以适应无线传感器网络对时间同步的快速收敛性、低能耗、鲁棒性及可扩展性等要求.无线传感器网络除了具备一般的无线通信网络的特点外,还具有节点密度高等特点. EGA充分利用这些特点,当一对节点在进行时间信息交换时,处在它们广播域的许多节点也会接收到它们发送的时间消息,这些节点对接收到的信息和自己当前的时钟消息进行平均,将此平均值作为自己的时钟更新值.这样的过程在每对邻居节点之间依次反复进行,最终会使网络中的所有节点同步于一个相同的时间值.
| [1] | Simeone O, Spagnolini U, Bar-Ness Y, et al. Distributed synchronization in wireless networks[J].IEEE Signal Processing Magazine, 2008, 25(5): 81–97. doi: 10.1109/MSP.2008.926661 |
| [2] | Ganeriwal S, Kumar R, Srivastava M B. Timing sync protocol for sensor networks [C]//First International Conference on Embedded Network Sensor Systems. New York, USA:ACM, 2003: 138-149. |
| [3] | Maggs M K, Okeefe S G, Thiel D V. Consensus clock synchronization for wireless sensor networks[J].IEEE Sensors Journal, 2012, 12(6): 2269–2277. doi: 10.1109/JSEN.2011.2182045 |
| [4] | Wu Jianshe, Jiao Licheng, Ding Ranran. Average time synchronization in wireless sensor networks by pairwise messages[J].Computer Communications, 2012, 35(2): 221–233. doi: 10.1016/j.comcom.2011.09.007 |
| [5] |
师超, 仇洪冰, 陈东华, 等. 一种简单的无线传感器网络时间同步方案[J]. 西安电子科技大学学报, 2013, 40(1): 93–99.
Shi Chao, Qiu Hongbing, Chen Donghua, et al. A simple distributed time synchronization scheme for wireless sensor networks[J].Journal of Xidian University, 2013, 40(1): 93–99. |
| [6] | Horn R A, Johnson C R. Matrix analysis[M]. Cambridge University Press, 1985: 12-89. |
| [7] |
李燕君, 叶敬川, 朱艺华. 能量感知的传感器网络分布式时空相关数据收集方案[J]. 北京邮电大学学报, 2011, 34(5): 110–114.
Li Yanjun, Ye Jingchuan, Zhu Yihua. An energy aware distributed protocol for spatial-temporal ocrrelated data gathering in wireless sensor networks[J].Journal of Beijing University of Posts and Telecommunications, 2011, 34(5): 110–114. |


