针对认知双向中继网络下信道状态信息不理想的情况, 提出了基于信干噪比(SINR)平衡的分布式鲁棒波束成形算法.该算法的最优波束成形因子在满足中继总功率和主用户接收端干扰功率受限的条件下, 使认知用户在最差情况下的SINR最大化.通过使用S-Procedure, 并引入半正定松弛思想, 可将原优化问题转化为凸优化可行性问题进行求解.仿真结果表明, 该算法可有效降低认知用户对主用户接收端的干扰, 保证主用户的正常通信, 验证了该算法的有效性和鲁棒性.
A distributed Robust relay beamforming design in cognitive two-way relay networks by consi-dering imperfect channel state information was proposed to improve the minimum worst-case signal-to-interference-plus-noise ratio (SINR) of two cognitive users, satisfying a total relay power constrains and keeping the interference at primary user receiver below an acceptable threshold. Based on S-Procedure, the non-convex problem is transformed into a convex feasibility problem by relaxing the rank constrains, which can be solved efficiently. Simulations show that the proposed design can satisfy both total relay power constrains and interference temperature constrains, and verify the effectiveness of the proposed method as well in comparison to the non-Robust relay beamforming technique.
为提高频谱资源利用率,Mitola博士提出了认知无线电(CR, cognitive radio)的概念[1].通过使用波束成形,可有效减小认知用户对主用户干扰以及认知用户之间干扰,提高系统吞吐量.同时,将中继协作技术用于CR网络可对抗信道衰落,提高频谱利用率.目前已有的关于认知中继网络的波束成形研究工作大多基于已知理想的信道状态信息(CSI, channel state information)的假设[2],Safavi等[3]指出非理想的CSI会严重影响网络的性能; Tao等[4]研究了非认知环境下反馈信道存在误差时的鲁棒波束成形设计问题; Ubaidulla等[5]研究了最小化均方误差的分布式鲁棒波束成形算法.
笔者考虑通信信道存在反馈误差的情况,在满足中继发送功率和主用户干扰功率受限的条件下,提出最大化认知用户最差情况下SINR的分布式鲁棒波束成形设计,并给出仿真结果.
1 系统模型分布式认知双向中继网络系统模型如图 1所示.认知用户在不影响主用户正常通信的条件下,与主用户共用同一频谱.在认知网络中,1对认知用户通过K个中继交互信息.每个节点都配置1根天线.认知用户的通信过程分为多址接入(MAC, multiple access)阶段和广播(BC, broadcast)阶段.
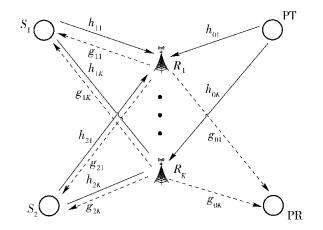
|
图 1 分布式认知双向中继网络系统模型 |
在MAC阶段,认知用户S1和S2同时向K个中继节点发送信号,同时,中继会接收到来自主用户发射端(PT, primary transmitter)的信号,所有中继节点的接收信号可表示为
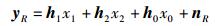
|
(1) |
其中:xi为Si的发送信号,E[|xi|2]=Pi,i∈{1, 2};x0为主用户发送端在MAC阶段的发送信号,E[|x0|2]=P0,信号x0、x1、x2是相互独立的;nR=[nR1, nR2, …, nRk]T,nRk为中继Rk端的加性噪声,nR=CN(0, σR2I);hi=[hi1, hi2, …, hik]T,i∈{1, 2},hik为认知用户Si到第k个中继Rk的信道系数;h0=[h01, h02, …, h0k]T,h0k为主用户发送端到中继Rk的信道系数;yR=[yR1, yR2, …, yRk]T, yRk为中继Rk端的接收信号.
在BC阶段,中继发送的信号可表示为
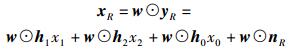
|
(2) |
其中:xR=[xR1, xR2, …, xRk]T;w为中继波束成形因子,w=[w1, w2, …, wk]T.中继发送功率为
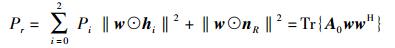
|
(3) |
其中: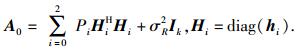
认知用户接收到来自中继的信号,表示为
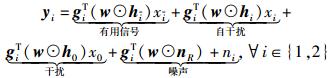
|
(4) |
其中:1=2,2=1;gi=[gi1, gi2, …, gik]T,gik为第k个中继到第i个认知用户的信道系数;ni为第i个认知用户端的加性噪声,ni=CN(0, σi2).
假设每个接收端可准确估计出本地接收CSI,即中继可准确估计出hi, i∈{0, 1, 2},主用户接收端(PR, primary receiver)和认知用户可知gi, i∈{0, 1, 2}.认知用户Si可以得到组合的信道和波束成形系数giT(w⊙hi),因此可将自干扰项从式(4) 中去除.
认知用户接收到的SINR可表示为
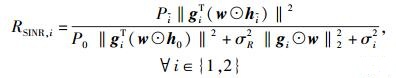
|
(5) |
中继对主用户接收端的干扰功率为
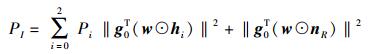
|
(6) |
其中:g0=[g01, g02, …, g0k]T,g0k为中继Rk到主用户接收端的信道系数.
放置在中继内部或中继附近的中心处理器搜集CSI向量hi、gi, i∈{0, 1, 2},并根据得到的信息设计波束成形因子.由于在实际通信过程中会存在量化误差和反馈时延,导致中心处理器无法得到理想的CSI向量gi, i∈{0, 1, 2}. CSI误差模型可表示为[6]
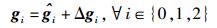
|
(7) |
其中: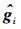
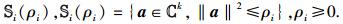
以最大化认知用户worst-case SINR为目标,在中继总发送功率受限和主用户接收端的干扰功率受限的条件下,设计鲁棒波束成形因子.
优化问题可以描述为问题1:
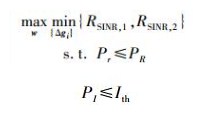
|
(8) |
其中:PR为中继发送总功率的最大值,Ith为主用户接收端所能容忍的干扰功率最大值.
通过引入辅助变量t,问题1可转化为问题2:
|
(9) |
式(9) 中SINR的约束条件为
|
(10) |
其中:

|
(11) |
式(10) 可进一步转化为
|
(12) |
其中
|
(13) |
其中:λi≥0为引入的松弛变量,∀i∈{1, 2};Qi= 
同理,式(9) 中PI的约束条件可转化为
|
(14) |
其中: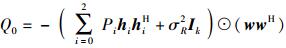
令W=wwH,问题2可转化为问题3:

|
(15) |
由于秩为1的约束条件,问题3是非凸的,通过去掉该约束条件,问题3变成易于求解的半正定规划(SDP, semidefinite programming)问题,最优的t值可用二分法求得.具体算法如下.
1) 初始化:
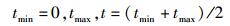
|
2) while |tmax-tmin|≥ε(精确度ε通常取10-3)
do
检查对于给定t值,问题3的可行性
if问题3可行
更新tmin=t t=(tmin +tmax)/2
else
更新tmax=t t=(tmin+tmax)/2
end if
end while
求解上述优化问题,验证所得最优解Wopt秩的值.当rank(Wopt)=1时,问题3的最优解可用特征值分解求得;当rank(Wopt)>1时,可用随机法或特征向量近似法求得[4].当认知用户数目不大于3时,通过半定规划松弛(SDPR, semidefinite programming relaxation)处理后的问题总存在满足秩为1的解[9],该算法的复杂度为

|
在仿真中,假设所有信道都是瑞利平坦衰落信道,即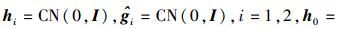
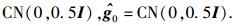
图 2所示为非理想CSI情况下,当干扰功率门限分别为Ith=-2 dB和Ith=2 dB时提出的鲁棒波束成形算法和文献[3]中非鲁棒波束成形算法的主用户接收端干扰功率随CSI误差ρ的变化曲线,仿真次数n=1 000.由图 2可以看出,当CSI存在误差时,不同干扰功率门限下,采用鲁棒波束成形算法的干扰功率都在预设的干扰功率门限值以下,而非鲁棒波束成形算法不能保证干扰功率受限的约束条件,并且对主用户产生的干扰随着误差的增大而增大.
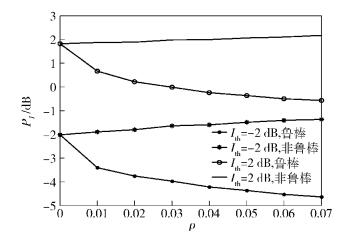
|
图 2 不同干扰功率门限(Ith=-2 dB, Ith=2 dB)下主用户接收端干扰功率随CSI误差变化曲线 |
图 3所示为不同CSI误差(ρ=0.01, ρ=0.04, ρ=0.07) 时提出的鲁棒波束成形算法和文献[3]中非鲁棒波束成形算法的主用户接收端干扰功率的累积分布函数(CDF, cumulative distribution function)曲线.仿真次数n=1 000,预设干扰功率门限值为Ith=1 dB.由图 3可以看出,当采用非鲁棒波束成形算法时,主用户接收端干扰功率会有50%左右不能满足干扰功率受限的约束条件,笔者提出的鲁棒波束成形算法都能满足干扰功率受限的条件,验证了当信道存在误差时鲁棒波束成形算法的有效性.
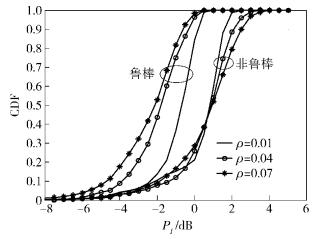
|
图 3 主用户接收端干扰功率的CDF曲线(Ith=1 dB) |
在认知双向中继网络中,当CSI非理想时,笔者提出的分布式鲁棒波束成形算法可使主用户接收端的干扰功率明显低于预设门限值,不会对主用户的正常通信造成干扰,具有重要的实际意义.仿真结果验证了该算法的有效性.由于采用认知双向中继,为便于研究,一般只考虑2个认知用户交互信息,对于多个认知用户下的鲁棒波束成形算法将在以后继续研究.
| [1] | Mitola J, Maguire G Q. Cognitive radio: making software radios more personal[J].IEEE Personal Communications, 1999, 6(4): 13–18. doi: 10.1109/98.788210 |
| [2] | Safavi S H, Sadeghzadeh R, Jamali V, et al. Interference minimization approach for distributed beamforming in cognitive two-way relay networks[C]//PACRIM. IEEE Pacific Rim Conference on Communications, Computers and Signal Processing. Victoria: [s.n.], 2011: 532-536. |
| [3] | Safavi S H, Ardebilipour M, Salari S. Relay beamforming in cognitive two-way networks with imperfect channel state information[J].IEEE Wireless Communication Letters, 2012, 1(4): 344–347. doi: 10.1109/WCL.2012.051112.120163 |
| [4] | Tao Meixia, Wang Rui. Robust relay beamforming for two-way relay networks[J].IEEE Communications Letters, 2012, 16(7): 1052–1055. doi: 10.1109/LCOMM.2012.050412.120481 |
| [5] | Ubaidulla P, Aissa S. Robust distributed two-way relay beamforming in cognitive radio networks[C]//ICT. 2012 19th International Conference on Telecommunications. Jounieh: [s. n. ], 2012: 1-6. |
| [6] | Zheng Gan, Wong K K, Paulraj A, et al. Robust collaborative-relay beamforming[J].IEEE Transactions on Signal Processing, 2009, 57(8): 3130–3143. doi: 10.1109/TSP.2009.2021456 |
| [7] | Pascual I A, Palomar D P, Perez-Neira A I, et al. A robust maximin approach for MIMO communications with imperfect channel state information based on convex optimization[J].IEEE Transactions on Signal Processing, 2006, 54(1): 346–360. doi: 10.1109/TSP.2005.861084 |
| [8] | Boyd S, Vandenberghe L. Convex optimization[M]. England: Cambridge University Press, 2004: 655. |
| [9] | Huang Yongwei, Zhang Shuzhong. Complex matrix decomposition and quadratic programing[J].Mathematics of Operations Research, 2007, 32(3): 758–768. doi: 10.1287/moor.1070.0268 |
| [10] | Sidiropoulos N D, Davidson T N, Luo Zhiquan, et al. Transmit beamforming for physical layer multicasting[J].IEEE Transactions on Signal Processing, 2006, 54(6): 2239–2251. doi: 10.1109/TSP.2006.872578 |


