2. 甘肃农业大学 工学院, 兰州 730070
针对在加密域中进行指纹匹配时指纹模板和现场样本整体对齐的困难性, 提出了一种免对齐的指纹匹配方案.采用具有旋转和平移不变性的细节点纹线方向特征和细节点局部结构, 设计实现了相应的加密二进制电路, 使得服务器能验证用户指纹, 而不会泄露各自的数据.实验结果表明, 所提方案在FVC2002-DB2指纹库上具有较高的匹配精度.
2. Engineering College, Gansu Agricultural University, Lanzhou 730070, China
When a server authenticates users based on fingerprint over open network, the process of fingerprint matching is usually handled in the encrypted domain with purpose of protecting the privacy and security of both parties. However, an accurate alignment of the template and the query sample is rather difficult in this situation. An alignment-free fingerprint-matching scheme was presented, which extracts two kinds of local features around the minutiae, ridge orientation and minutiae local structure. Both features have the properties of invariant to rotation and translation. Garbled circuits were designed to implement the corresponding matching algorithm, which allow the server to verify the user without leaking the respective data. Experiment shows that the scheme achieves a relatively higher accuracy on FVC2002-DB2 public database.
在开放网络中进行基于生物特征识别的身份认证时,面临的一个重要挑战是,认证的双方——服务器和用户往往相互不信任,双方只要认证结果,但并不想让对方知道自己私有的生物特征数据.而传统方法中,运行在服务器或客户端的识别程序需要将预先存储的模板和用户的现场生物特征放在一起进行匹配,从而得到认证结果,这就需要知道双方的数据.为了解决数据隐私性和开放网络环境下认证的矛盾,一些解决方案采用了密码术中的同态加密[1]和加密二进制电路(GC, garbled circuit)[2].一些研究者将这些技术结合指纹[3-4]设计了匹配协议,以实现远程身份认证.
上述文献均采用全局指纹特征,这样需要将模板和现场指纹特征进行预对齐.但目前的预对齐方案对图像质量要求很高,对齐精度则难以保证[5].为了避免进行预对齐,采用具有旋转和平移不变性的局部指纹特征,利用GC设计具有隐私保护的认证方案,无须预对齐.但单一局部特征存在识别精度不高的缺点,故采用了基于细节点局部纹线方向特征和细节点局部结构互相补充,以解决精度和隐私保护的矛盾.
1 特征选取与匹配算法采用的两种特征均以细节点为中心:细节点纹线方向特征描述了细节点周围纹理特征[6],而细节点局部结构则反映了局部的细节点分布特点[7],两者在描述指纹的局部特征方面可以互为补充.记细节点模板MT={(xiT, yiT, θiT)|1≤i≤NT},现场样本细节点集合MQ={(xiQ, yiQ, θiQ)|1≤i≤NQ}.
1.1 细节点纹线方向特征Tico等[6]提出细节点纹线方向描述子,它以细节点平面坐标为圆心,在其周围画L个半径rl(1≤l≤L)同心圆,在每个圆周上均匀取Kl个采样点pk, l(1≤k≤Kl).以细节点方向为参考,这些点逆时针方向排列,每个圆上的第1个点为细节点方向延长线和该圆的交点.估计出pk, l的局部纹线方向,可以定义细节点纹线特征为:o={{{λ(θk, l, θ)}k=1Kl}l=1L,其中λ(θk, l, θ)}为θk, l相对于θ的角度.
记miT和mjQ为MT和MQ中的两个细节点,它们的纹线特征分别记为o(miT)={αk, li}和o(mjQ)={βk, lj},则它们之间的相似性函数定义为
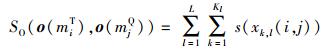
|
(1) |
其中x()为相对角度:
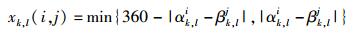
|
(2) |
s(x)为相似值,Tico认为其最优形式是exp()函数,但它无法用GC实现,取如下便于GC实现的符号函数形式
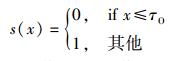
|
(3) |
其中τO为一预设阈值.显然,若两个纹线方向特征相似,则SO取值就较小.
1.2 细节点局部结构考虑GC实现的复杂性,采用尽可能少的细节点构造局部结构,具体特征构造如图 1所示.图中m1为参考细节点,计算其邻域内的细节点m2与m1之间的长度l,m2与m1的相对方向φ以及m2的方向与两个细节点连线的夹角ϕ,可构造细节点局部特征向量d=[l, φ, ϕ].

|
图 1 细节点局部结构 |
对于miT∈MT和mjQ∈MQ,记它们的局部特征分别为d(miT)=[liT, φiT, ϕiT],d(mjQ)=[ljQ, φjQ, ϕjQ].则作者定义的两者之间的相似性函数为
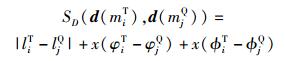
|
(4) |
其中x()为相对角度
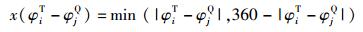
|
(5) |
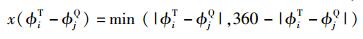
|
(6) |
显然,两个细节点局部结构特征相似,则SD取值就较小.
1.3 匹配算法设由MT构造出的纹线特征和局部结构特征集合分别为OT={o(miT)|1≤i≤NT}和DT={d(miT)|1≤I≤NT},由MQ构造出的纹线特征和局部细节点结构特征集合分别为OQ={o(miQ)|1≤i≤NQ}和DQ={d(mjQ)|1≤j≤NQ}.为判断模板和现场指纹的匹配程度,作者对OT和OQ以及DT和DQ中的元素进行逐点比较,形成两个NT×NQ的矩阵UO和UD,它们的索引(i, j)分别代表模板和现场指纹的局部特征,UO(i, j)的值由式(1) 计算得到,UD(i, j)的值由式(4) 计算得到. UO中的第i行表示模板中o(miT)与OQ中每个元素的相似性,值越小相似程度越高,可取第i行的最小值与预设阈值τSO进行比较,若小于则认为在OQ中存在一个与o(miT)匹配的特征. OT和OQ的相似度得分可按下式计算
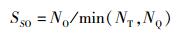
|
(7) |
其中NO是OT和OQ中匹配的特征总数量.
同理,取UD第i行的最小值与预设阈值τSD进行比较,若小于则认为在DQ中存在一个与d(miT)相似的特征.采用式(8) 计算DT和DQ的相似度得分
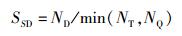
|
(8) |
其中ND是DT和DQ中相似特征的总数量.
最后,计算模板和现场指纹的相似度总得分为
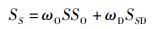
|
(9) |
其中ωO和ωD为权重因子,可由实验确定.由SS可以得到模板和现场指纹的匹配程度,其值越高,两者越匹配,由SS可以计算出接受者操作特性(ROC,receiver operating characteristic)曲线.
2 匹配算法的GC实现在认证模型中,服务器持有{OT, DT },而用户输入为{OQ, DQ },双方交互计算SS,但各自的数据不能泄露给对方,且SS的结果只能由服务器知道,用户不能获知.安全模型采用半诚实模型(semi-honest model),即双方依照认证协议执行各自任务,但可保留交互过程中的中间数据,以此分析对方数据.采用GC实现上节中匹配算法. GC的特点是首先设计完成特定功能的二进制门电路,服务器对于电路的每一条线(位)分配一个二进制加密值(garbled value),电路输入输出的关系由garbled表描述而非真值表.服务器将自己输入对应的garbled值以及garbled表发送给用户.用户的输入则通过不经意传输协议(OT,oblivious transfer)[8]获得对应的garble值,而服务器不知道用户真实数据.用户根据双方的garbled值和garbled表,计算电路输出的garble值,该值回送服务器后,由服务器解密即可得到真实数值.
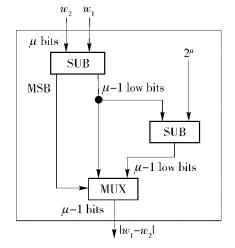
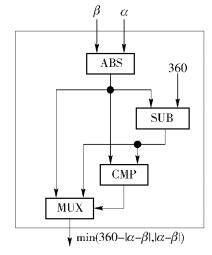
2.1 基本GC模块Kolesnikov等[9]给出了一些基本的GC模块,如加法器(ADD)、减法器(SUB)、选择器(MUX)、比较器(CMP).在此基础上,设计了能实现匹配算法的电路. 图 2给出的电路ABS以μ位w1和w2二进制数为输入,输出o为| w1-w2|.图中SUB为减法器,其输入为有符号数,以补码形式表示[9],最高位(MSB)为符号位. 图 3给出了相对角度的计算电路ROD,α和β为输入的角度,其输出为|α-β|和360-|α-β|中较小数.
|
图 2 绝对值电路ABSs |
|
图 3 相对角度计算电路ROD |
图 4给出了根据式(1) 计算两个纹线特征相似函数电路SOC的结构,它的输入是两个纹线特征o(miT)={αk, li}和o(mjQ)={βk, lj}.图中每个CMP计算式(3) 的符号函数,由于它的输出只有1位,为减少电路复杂度,不采用普通加法器计算式(1) 中连加,而采用文献[4]中的计数器电路COUNTER对“1”的数量进行累加.

|
图 4 纹线方向特征相似函数计算电路SOC |
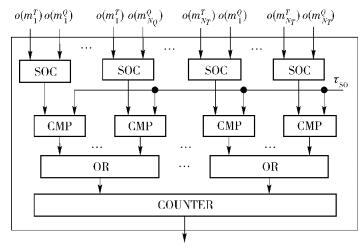
图 5给出了模板和现场指纹的相似性得分计算电路SSOC,其输入是模板纹线特征集合OT和现场指纹纹线特征集合OQ,由于GC的除法电路非常复杂,故该电路只输出两个集合中匹配上的纹线特征的总数量NO,用户将NO的garbled值传给服务器后,由后者解密得到真实值后根据式(7) 计算得分SSO.为简单起见,图 5只画出了计算矩阵UO的第1行和最后一行的电路,其他省略,用…表示.此外,因为求NQ个数最小值的电路复杂度高于NQ个比较电路,且实际上无需知道o(miT)在OQ中确切的匹配特征的索引,为降低电路的复杂度,图 5的电路没有采用1.3节中的先搜索矩阵UO每行最小值,然后与阈值τSO比较的方法,而是将每行的NQ个SOC的输出直接与τSO比较,所有结果进行或运算,对NT行的结果进行计数就可以得到NO.
|
图 5 匹配上的纹线方向特征数量计算电路SSOC |
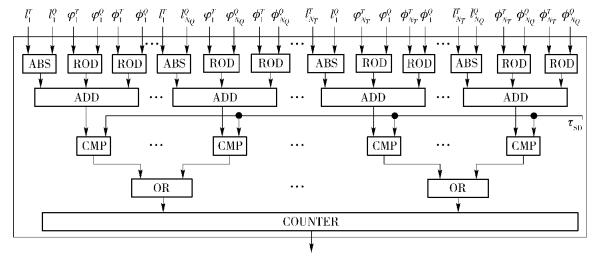
图 6给出了计算模板和现场样本的细节点局部结构特征匹配数量的电路SSDC,图中只画出了计算矩阵UD的第1行和最后一行的电路,其他省略,用…表示.矩阵元素代表相似值,由计算式(4) 而得到,图 6中由一个ABS,两个ROD和一个ADD电路计算.与纹线匹配类似,对于矩阵每一行相似值,不搜索最小值,而是直接与阈值τSD比较后,经OR电路,最后送计数器COUNTER确定匹配上的细节点局部结构数量ND.该值的garbled值被用户送到服务器后,由后者根据式(8) 计算得分SSD.最后模板和现场指纹的总得分由服务器根据式(9) 计得到.
|
图 6 匹配上的细节点局部结构数量计算电路SSDC |
在MyEclipse 10环境中开发了相应的Java程序实现上述匹配电路所对应的GC,使用了Huang等[10]开发的GC Java库,并在FVC2002-DB2指纹库上按照FVC2002竞赛规则测试了真实接受率GAR(genuine accept rate)和认假率FAR(false accept rate).该库有800幅指纹图像,图像大小为296×560像素.由于GC只能进行整数计算,故需要对各特征数据作量化处理,用7位表示一个数据,将两种特征的每个分量线性映射成[0,127]的整数.一些主要参数选择如下:1) 对于纹线特征,L=3,r1=30,r2=48,r3=66,K1=10,K2=16,K3=22,τO=6;2) 对于局部细节点结构,lmin=20,lmax=90,τSD=22.这些参数由经验选择. GC的参数选择如下:每个门的每根导线采用80位garbled值、统计安全参数为80位.计算环境为1台Dell商用机(CPU为英特尔酷睿i3-2120处理器3.30 GHz,内存8 G DDR3) 和1台Dell服务器,100 M局域网.
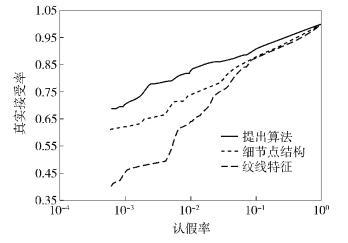
图 7给出了由GC实现的提出算法在FVC2002-DB2上的ROC曲线,作为对比,作者还分别测试了纹线特征和细节点结构单独匹配时的ROC曲线.从图中可以看出细节点结构的匹配性能优于纹线特征,而提出算法将两种特征在得分层进行融合,提高了匹配性能,3种方法的等错误率分别为:9.1%(提出算法),11.5%(细节点结构),12.9%(纹线特征).由GC实现的提出算法运行时间比较长,在FVC2002-DB2上两枚指纹进行匹配的平均时间是217.4 s,该时间包括OT协议和GC的执行的总时间,但不包括OT协议和GC的初始化的时间.
|
图 7 提出方法在FVC2002-DB2上的ROC曲线 |
几乎所有基于全局特征的指纹匹配均需要将两枚指纹对齐,而这需要复杂的算法.采用两种细节点周围的局部特征:纹线特征和局部结构作为匹配依据,这些特征具有旋转和平移不变性,对图像质量不高的指纹也能适用.作者用GC实现了两种特征的匹配算法,并在公开指纹数据库FVC2002-DB2上进行了性能测试,实验结果表明提出方法有较高的精确度,但运行时间较长.由于提出方法中,很多电路都是并行工作的,可以考虑采用现场可编程门阵列(FPGA,field programmable gate array)实现GC,以减少运行时间.
| [1] | Rappe D K. Homomorphic cryptosystems and their applications [D]. Dortmund, Germany: University of Dortmund, 2004. |
| [2] | Lindell Y, Pinkas B. A proof of Yao's protocol for secure two-party computation[J].Journal of Cryptology, 2009, 22(2): 161–188. doi: 10.1007/s00145-008-9036-8 |
| [3] | Huang Yan, Malka L, Evans D, et al. Efficient privacy-preserving biometric identification [C]//18th Network and Distributed System Security Conference, San Diego, California: Internet Society, 2011: 6-9. |
| [4] |
冯全, 杨梅, 康立军, 等. 基于二进制加密电路的指纹细节点匹配[J]. 四川大学学报:工程科学版, 2013, 45(2): 75–80.
Feng Quan, Yang Mei, Kang Lijun, et al. Minutiae matching based on garbled circuits[J].Journal of Sichuan University: Engineering Science Edition, 2013, 45(2): 75–80. |
| [5] | Nandakumar K, Jain A K, Pankanti S. Fingerprint-based fuzzy vault: implementation and performance[J].IEEE Trans. on Information Forensics and Security, 2007, 2(4): 744–757. doi: 10.1109/TIFS.2007.908165 |
| [6] | Tico M, Kuosmanen P. Fingerprint matching using an orientation-based minutia descriptor[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(8): 1009–1014. doi: 10.1109/TPAMI.2003.1217604 |
| [7] | Kisel A, Kochetkov A, Kranauskas J. Fingerprint minutiae matching without global alignment using local structures[J].INFORMATICA, 2008, 19(1): 31–44. |
| [8] | Naor M, Pinkas B. Efficient oblivious transfer protocols [C]//Twelfth Annual ACM-SIAM Symposium On Discrete Algorithms (SODA), Washinton DC, Association for Computing Machinery, Inc., 2001: 448-457. |
| [9] | Kolesnikov V, Sadeghi A, Schneider T. Improved garbled circuit building blocks and applications to auctions and computing minima[C]//8th International Conference on CANS'09, Kanazawa, Japan: Springer, 2009: 1-20. |
| [10] | Huang Yan, Evans D, Katz J, et al. Faster secure two-party computation using garbled circuits [C]//20th USENIX Security Symposium, San Francisco, California: USENIX Association, 2011: 1-16. |


