针对当前直接匿名认证(DAA)方案设计复杂度高、计算开销大, 导致制约资源受限的嵌入式或移动可信智能设备的应用的现状, 提出了一种改进DAA方案.采用双线性对密码体制, 以双线性对为工具, 以q强Diffie-Hellman、判定性Diffie-Hellman安全假设为基础.分析结果表明, 该方案在确保正确、安全、匿名的基础上, 计算开销得到了有效降低, 解决了当前资源受限可信设备的计算瓶颈问题, 加速推进了DAA方案在移动领域的应用.
Considering the current directory anonymous attestation (DAA) scheme complicated and time-consuming, which makes it limited in resource-constrained devices such as embedded, an improved DAA scheme is proposed. This scheme is based on bilinear pairing under the assumption of q strong Diffie-Hellman and decisional Diffie-Hellman. The analysis shows that this scheme is not only correct, security and anonymous, but also efficiently relieves the computation cost. This scheme further solves the computation bottleneck and accelerate application for DAA in mobile field.
DAA机制的概念和具体方案[1]由Brickell等首次提出,可信计算组织(TCG, trusted computing group)[2]将其纳入可信平台模块(TPM, trusted platform module)[3-4]规范.随后一系列的改进方案[5-15]被提出,其中文献[5, 15]的方案是基于RSA密码体制设计的,给资源受限的可信设备带来计算和空间上的瓶颈.因此,一系列的基于椭圆曲线密码体制(ECC, elliptic curves cryptography)的双线性映射为密码学工具的方案[6-12]被提出,效率有所改进.文献[6-8, 10]方案的安全性基于LRSW假设[16],尽管文献[8]方案需要更少的计算开销,但该方案存在验证者不能识别恶意TPM安全隐患.文献[9, 11-13]方案的安全性基于q强Diffie-Hellman(q-SDH, q strong Diffie-Hellman)假设[17],计算复杂度有所改善,但对于嵌入式设备,依然受限.近几年,针对Mobile、M2M的DAA方案[14-15]相继被提出.文献[14]的方案无法证实加入协议的正确性,文献[15]的方案是基于RSA设计的,运算效率较低.笔者针对现有方案存在的一些不足之处,提出一种改进的DAA方案.该方案以双线性对为工具,基于q-SDH和判定性Diffie-Hellman(DDH, decisional Diffie-Hellman)安全假设,其满足现有方案正确性、安全性和匿名性的同时,计算开销得到了进一步的降低,促进可信计算在资源受限移动、物联网等智能可信设备领域的应用.
1 预备知识1.1 双线性映射定义1[18] 令G1、G2和GT为3个乘法循环群,阶均为素数p,其生成元分别为g1、g2和e(g1, g2).若满足以下3条性质,那么映射e:G1×G2→GT称为双线性对.
1) 双线性:任意u∈G1, v∈G2,a、b∈Zp,满足e(ua, vb)=e(u, v)ab;
2) 非退化性:e(g1, g2)≠1;
3) 可计算性:任意u∈G1, v∈G2,均存在有效算法计算e(u, v).
1.2 q-SDH假设定义2[17] 令G1和G2是2个乘法循环群,阶均为素数p,其生成元分别为g1和g2,输入一个(q+2) 元组(g1, g2, g2r, g2(r2), …, g2(rq)),输出(g11/(r+x),x),其中x,r∈Zp*.如果Pr[A(g1, g2, g2r, g2(r2), …, g2(rq))=(g11/(r+x), x)]≥ε,那么算法A是以概率ε的优势解决q-SDH问题的.其中,概率的计算基于随机选择r∈Zp*以及随机选择的任意多项式时间算法A.如果概率ε是可以忽略的,则称q-SDH问题是难解的.
1.3 DDH假设定义3 令G是一乘法循环群,阶为素数p,生成元为g,输入g、ga、gb、gc∈G,对于任意未知的a、b、c∈Zp*,如果满足ab=c,输出1;否则,输出0.如果|Pr [g∈G, a、b∈Zp*:A(g, ga, gb, gab)=1]- Pr [g∈G, a、b、c∈Zp*:A(g, ga, gb, gc)=1]|≥ε,则称算法A以概率ε的优势解决DDH问题.其中,概率的计算基于随机选择a、b、c∈Zp*以及随机选择的任意多项式时间算法A.如果概率ε是可以忽略的,则称DDH问题是难解的.
2 改进的DAA方案DAA机制由初始化、DAA加入协议、DAA签名协议和签名验证4部分组成.
2.1 初始化输入安全参数{0, 1}t, 其中t为安全参数的长度,初始化算法流程如下.
步骤1 选择2个互异的阶为大素数p的乘法循环群G1、G2和双线性映射e:G1×G2→GT,g1、g2和(g1, g2)分别是G1、G2和GT的生成元.
步骤2 选择x、y∈Zp*并计算X:=g2x和Y:=g2y.
步骤3 选择5个Hash函数:H1:{0, 1}*→Zp,H2:{0, 1}*→Zp,H3:{0, 1}*→G1,H4:{0, 1}*→Zp,H5:{0, 1}*→Zp.
步骤4计算A:=g1y输出DAA机制公钥PK和发布者私钥ISK:
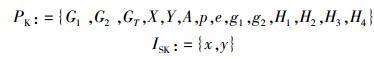
|
加入协议在信息交互过程中涉及3个参与方:TPM、主机和发布者.协议流程如下.
步骤1 发布者随机选择nI∈{0, 1}t,将nI发送给TPM.
步骤2 TPM收到nI后,首先计算TPM的隐私密钥f:=H1(DAAseed||cnt||KI)(DAAseed为TPM内部密钥种子,cnt为用来跟踪TPM执行加入协议次数的计数器,KI为认证公钥PK的发布者长期公钥),计算D:=Af;然后随机选择lf∈Zp,计算R:=Alf,c1:=H2(PK‖nI‖D‖R),kf:=lf+c1f(mod p);最后将(D, c1, kf, nI)发送给发布者.
步骤3 发布者收到消息后,首先验证nI的正确性并依据D和恶意TPM列表检测该TPM的合法性;然后计算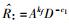
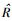
步骤4 TPM信任状cre传递给主机.
步骤5 主机计算验证e(g1D, X)=e(C, g2)是否成立,如果验证失败,则终止协议.
2.3 签名协议签名协议涉及2个参与方:TPM和主机.签名协议流程如下.
步骤1 判断bsn,若bsn=⊥, TPM则选择B←G1;否则TPM计算B:=H3(bsn),选择bsn的作用参考文献[8].接下来TPM选择rf←Zp并计算K:=Arf,然后将(K, B)发送给主机.
步骤2 主机收到消息后随即选择a←Zp,计算T1:=g1a,T2:=Aa,T3:=Ca,T4:=Da,ch:=H4(PK‖B‖K‖T1‖T2‖T3‖T4‖nV)(nV为从验证者获取的随机数),并将ch发送给TPM.
步骤3 TPM收到消息后随机选择nT∈{0, 1}t,计算c2:=H5(ch‖nT‖m)(m为签名的平台状态消息),sf:=rf+c2f(mod p),然后将(c2, nT, sf)发送给主机.
步骤4 主机计算σ:=(B, K, T1, T2, T3, T4, c2, nT, sf)作为签名.
2.4 签名验证签名验证算法中需要输入的参数包括签名的平台状态消息m、bsn、nV、DAA公钥PK、签名(B, K, T1, T2, T3, T4, c2, nT, sf)和恶意TPM秘密密钥列表L,验证流程如下.
步骤1 验证B、K、T1∈G1和sf∈Zp是否成立.
步骤2 验证所有的f′∈L,是否存在T2f′=T4,若存在,则为恶意TPM,终止协议,否则执行下一步.
步骤3 计算K′:=AsfD-c.
步骤4 验证c2=H5(H4(PK‖B‖K′‖T1‖T2‖ T3‖T4‖nV)‖nT‖m)是否成立,如果不成立,终止协议.
步骤5 验证e(T1T2, X)=e(T3, g2)和e(T1, Y)=e(T2, g2)是否成立,如果不成立,终止协议.
3 方案分析3.1 正确性方案的正确性主要体现在2方面:一是加入协议中发布者对可信平台的验证;二是验证者对可信平台的验证.
3.1.1 加入协议正确性证明验证R=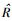
因为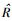
验证K=K′、e(T1T2, X)=e(T3, g2)和e(T1, Y)=e(T2, g2)是否成立.
因为
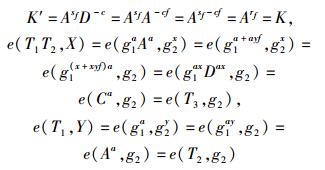
|
即签名协议正确性成立.
3.2 安全性方案的安全性分析包括4个方面:秘密信息f的保密性、防恶意TPM欺骗性、匿名性和签名不可伪造性.
1) 秘密信息f的保密性:秘密信息f的保密性至关重要,f的安全性直接关系到DAA协议的可信性.考虑到可信平台的主机安全级别低于TPM,协议中凡涉及f的所有运算由TPM来完成.必要时,TPM以零知识证明的方式证明其拥有秘密信息f.因此,协议确保了秘密信息f的保密性.
2) 防恶意TPM欺骗性:DAA方案应具备抗恶意TPM的欺骗攻击,方案在加入协议和签名验证中均对TPM的合法性进行了验证.在加入协议中,TPM将D=Af发送给发布者后,发布者依据恶意TPM密钥列表中所有的fi判断是否存在D=Afi,进而判断该TPM是否为非法的;在签名验证中,验证者收到签名后,验证者依据恶意TPM密钥列表中所有的fi判断是否存在T2fi=T4,进而判断该TPM是否为非法伪造的.
3) 匿名性:DAA方案应具备匿名性,方案在签名协议中,主机对发布者发布的信任状cre:=(C)进行了盲化,然后计算出签名σ:=(B, K, T1, T2, T3, T4, c2, nT, sf).显然,验证者和发布者之间无任何相同的信息,即使二者合谋也无法得知具体TPM,因此满足平台不可连接跟踪性和匿名性需求.
4) 签名不可伪造性:DAA方案的签名应具备不可伪造性,本方案签名的不可伪造性包含2个方面.一个是加入协议中信任状不能伪造:发布者使用自己的私钥x计算C:=g1xDx生成信任状,可信计算平台收到信任状后,用发布者公钥X验证e(g1D, X)=e(C, g2)是否成立,进而可以确定Issuer是否伪造了信任状;另一个是签名协议中签名不能伪造:可信平台收到发布者的信任状后,对其盲化并生成自己的签名,在签名验证协议过程中需向验证者零知识证明可信计算平台拥有发布者颁发的信任状,因此,可信平台在安全假设基础上无法伪造合法的签名.
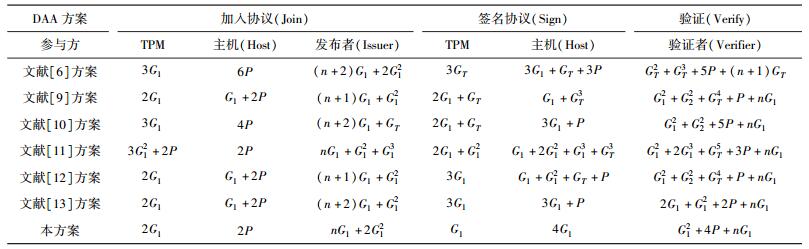
3.3 有效性本方案是在现有方案基础上进行的改进,尤其是基于双线性对的一些方案,因此仅与基于双线性对的DAA方案对比分析本方案的效率.文献[6]与文献[7]中的方案相同;文献[8]在效率方面有明显改进,但其在签名协议过程中存在安全隐患;文献[14]方案的加入协议的正确性无法证实.因此,在表 1中仅与文献[6, 9-13]的方案与本方案进行效率对比分析.方案初始化仅仅计算一次,并可以提前离线完成.因此,在表 1中,仅比较方案的加入协议(包括TPM、Host和Issuer)、签名协议(包括TPM和Host)和验证算法的计算量.
|
|
表 1 基于双线性对DAA方案计算费用比较 |
表 1中,Gi(i∈{1, 2, T})表示在群Gi中的指数运算复杂度,Gim表示在群Gi中m个指数乘法运算复杂度,P表示双线性对计算复杂度,n表示恶意TPM列表中密钥个数.在比较列表中,约定所有方案的发布者和验证者均对TPM的合法性进行检测.
方案的计算性能尤其关心TPM的运算量,其次是Host、Verifier和Issuer. 表 1显示,本方案的最大优势是TPM的计算量明显降低,其他参与方的运算量同样有不同幅度的减少.
4 结束语针对现有DAA方案算法复杂,计算复杂度高的问题,提出了一种改进的基于双线性对的DAA方案.通过性能分析,该方案在具备现有方案的正确性和安全性基础上,降低DAA方案中的运算复杂量,尤其是TPM的计算量得到了较大优化,使其更好地适应TPM的低处理速度和低智能嵌入式、移动和物联网等资源受限的可信环境,极大地扩展了可信计算技术的应用空间.
| [1] | Brickell E, Camenisch J, Chen Liqun. Direct anonymous attestation[C]//In Proceedings of the 11th ACM Conference on Computer and Communications Security. New York: ACM Press, 2004: 132-145. |
| [2] | Trusted Computing Group. ISO15408—2007, TCG Specification Architecture Overview[S]. |
| [3] | Trusted Computing Group. ISO/IEC11889—2007, TPM Main, Part 1: Design Principles[S]. |
| [4] | Pearson S, Balacheff B, Chen Liqun, et al. Trusted computing platforms: TCPA technology in context[M]. Upper Saddle River: Prentice Hall Press, 2002: 1-352. |
| [5] | Ge He, Tate S R. A direct anonymous attestation scheme for embedded devices[C]//Hutchison D, Kanade T, Kleinberg J M, et al. LNCS. Heidelberg: Springer, 2007: 16-30. |
| [6] | Brickell E, Chen Liqun, Li Jiangtao. A new direct anonymous attestation scheme from bilinear maps[C]//Hutchison D, Kanade T, Kleinberg J M, et al. LNCS. Heidelberg: Springer, 2008: 166-178. |
| [7] | Brickell E, Chen Liqun, Li Jiangtao. Simplified security notions of direct anonymous attestation and a concrete scheme from pairings[J].International Journal of Information Security, 2009, 8(5): 315–330. doi: 10.1007/s10207-009-0076-3 |
| [8] | Chen Liqun, Morrissey P, Smart N P. Pairings in trusted computing[C]// Hutchison D, Kanade T, Kleinberg J M, et al. LNCS. Heidelberg: Springer, 2008: 1-17. |
| [9] | Chen Liqun. A DAA scheme requiring less TPM resources[C]// Hutchison D, Kanade T, Kleinberg J M, et al. LNCS. Heidelberg: Springer, 2009: 111-125. |
| [10] | Chen Liqun, Morrissey P, Smart N P. DAA: fixing the pairing based protocols[Z]. Cryptology ePrint Archive, Report 2009/198, 2009. |
| [11] | Chen Xiaofeng, Feng Dengguo. Direct anonymous attestation for next generation TPM[J].Journal of Computers, 2008(12): 43–50. |
| [12] | Brickell E, Li Jiangtao. A pairing-based DAA scheme further reducing TPM resouses[C]// Hutchison D, Kanade T, Kleinberg J M, et al. LNCS. Heidelberg: Springer, 2010: 181-195. |
| [13] |
宋成, 孙玉琼, 彭维平, 等. 改进的直接匿名认证方案[J]. 北京邮电大学学报, 2011, 34(3): 62–65.
Song Cheng, Sun Yuqiong, Peng Weiping, et al. Improved direct anonymous attestation scheme[J].Journal of Beijing University of Posts and Telecommunications, 2011, 34(3): 62–65. |
| [14] | He Yingying, Chen Liquan, Wang Lingling. An improved direct anonymous attestation scheme for M2M networks[J].Elsevier Procedia Engineering, 2011, 5: 1481–1486. |
| [15] | Zhang Dedong, Ma Zhaofeng, Niu Xinxin, et al. Anonymous authentication scheme of trusted mobile terminal under mobile Internet[J].The Journal of China Universities of Posts and Telecommunications, 2013, 20(1): 58–65. doi: 10.1016/S1005-8885(13)60008-4 |
| [16] | Lysyanskaya A, Rives R L, Sahai A, et al. Pseudonym systems[C]// Hutchison D, Kanade T, Kleinberg J M, et al. LNCS. Heidelberg: Springer, 2000: 184-199. |
| [17] | Boneh D, Boyen X. Short signatures without random oracles[C]//Hutchison D, Kanade T, Kleinberg J M, et al. LNCS. Heidelberg: Springer, 2004: 56-73. |
| [18] | Boneh D, Boyen X, Shacham H. Short group signatures[C]//Hutchison D, Kanade T, Kleinberg J M, et al. LNCS. Heidelberg: Springer, 2004: 41-55. |